|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Marcus M., Minc H. — Survey of matrix theory and matrix inequalities |
|
|
 |
| Предметный указатель |
 -vector 2 -vector 2
 -square matrix 2 -square matrix 2
 th adjugate 16 th adjugate 16
(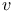 , ,  , ,  )-matrix 13 129 )-matrix 13 129
(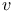 , ,  , ,  )-matrix, adjoint of 25 )-matrix, adjoint of 25
(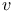 , ,  , ,  )-matrix, determinant of 25 )-matrix, determinant of 25
(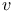 , ,  , ,  )-matrix, determinantal divisors of 42 46 )-matrix, determinantal divisors of 42 46
(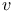 , ,  , ,  )-matrix, normality of 72 )-matrix, normality of 72
Adjoint, (adjugate) 13
Adjoint, (conjugate transpose) 5
Adjoint, reduced 125
Adjugate 13
Aitken, A. C. 89 90
Alternant matrix 15
Alternating multilinear function 13
Amir-Mo z, A. R. 89 z, A. R. 89
Arithmetic-geometric mean inequality 106
Aronszajn, N. 134
Arscott, F. 171
Augmented matrix 31
Basis 29
Basis, completion to 38
Beckenbach, E. F. 134 135
Bellman, R. 89 171
Bendixon’s theorems 140
Bendixson, I. 140 171
Bergstrom, H. 134
Bilinear functional 59
Bilinear functional, conjugate 59
Binet — Cauchy theorem 14
Binet — Cauchy theorem for permanents 20
Birkhoff, U. 07 136
Block multiplication 6
Block multiplication, examples 7
Bodewig, E. 89
Bonnesen 135
Brauer, A. 145 148 155 156 170 171
Brauer’s Theorem 145 155
Bromwich, T. J. I’a. 171
Browne, E. 89 143 144 148 171
Browne’s theorem 143 144
Bullen, P. 136
Cauchy inequalities 119
Cauchy — Schwarz inequality 61
Cayley parameterization 74
Cayley — Hamilton theorem 50
Characteristic matrix 21
Characteristic polynomial 21
Characteristic roots 22
Characteristic roots, algebraic multiplicity of 39
Characteristic roots, geometric multiplicity of 38
Characteristic vectors 39
Circulant 66
Circular matrix 75
Collar, A. R. 89
Collatz, L. 136 171
Column of a matrix 2
Column vector 2
Companion matrix 52
Compound matrix 16
Concave 102
Concave, strictly 102
Congruence 81
Conjugate transpose 5
Conjunctive matrices 84
Convex combination 96
Convex function 101
Convex hull 96
Convex matrix function 112
Convex polyhedron 96
Convex sets 93
Convex sum 96
Convex, strictly 102
Coordinate 2
CYCLE 11
Cycle, disjoint 11
Cycle, length of 11
Cycle, structure 11
De Bruijn, N. G. 9
Decomposable 122
Decomposable, partly 123
Derogatory 50
Desplanques, J. 140 146 171
Determinant 12
Determinant, expansion by row or column 13
Determinant, Laplace expansion of 14
Determinantal divisors 41
Diagonal 12
Diagonal, main 12
Diliberto, S. P. 9
DIMENSION 29
Direct product 8
Direct sum of matrices 5
Direct sum of vectors 7
Discrepancy of two vectors 111
Distinct representatives 18
Dmitriev, N. A. 171
Doubly stochastic 95 129
Drazin, M. A. 9
Duncan, W. J. 89
Dungey, J. W. 91
Dynkin, E. B. 171
Eaves, J. C. 90
Eggleston, H. G. 135
Eigenvalues 23
Elementary divisor 43
Elementary matrix 33 37
Elementary operations 32
Elementary operations, column 37
Elementary operations, row 32
Elementary symmetric function 10
Elementary symmetric function, weighted 106
Entry 2
Epstein 91
Equivalent matrices 42
Euclidean norm 18
Euclidean space 60
Faddeeva, V. N. 89
Fan, K. 134 136 152 171 172
Fan’s theorem 152
Farnell, A. B. 144 148 172
Farnell’s inequality 144
Fass, A. L. 89
Fenchel, W. 135
Ferrar, W. L. 89
Field of values 168
Finkbeiner, D. 89
Fischer, E. 134
Flanders, H. 91
Fr chet 159 172 chet 159 172
Fr chet’s theorem 159 chet’s theorem 159
Frazer, R. A. 89
Friedman, B. 91
Frobenius canonical form 53
Frobenius inequality 27
Frobenius theorem on commutativity 25
Frobenius theorem on nonnegative matrices 152
Frobenius, G. 136 144 172
Fuller, L. E. 89
Fully indecomposable 123
Functions of a matrix, arbitrary 73
Functions of a matrix, exponential 72
Functions of a matrix, normal 71
Functions of a matrix, polynomial 73
Functions of a matrix, square root 71
Gantmacher, F. R. 89 135 171
Gelfand, I. 89
Ger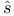 gorin discs 146 gorin discs 146
Ger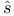 gorin, S. A. 140 145 146 172 gorin, S. A. 140 145 146 172
Ger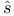 gorin’s theorem 146 gorin’s theorem 146
| Givens, W. 91 172
Gr bner, W. 89 bner, W. 89
Graeub, W. 89
Gram — Schmidt process 60
Grassmann product 17
Greatest common divisor 40
Grimshaw, M. E. 89 135
Gruenberg, K. W. 91
H lder inequality 108 lder inequality 108
Hadamard determinant theorem 114
Hadamard product 120
Hadamard, J. 140 146 171
Hadley, G. 89
Half-spaces, closed 94
Half-spaces, open 94
Halmos, P. R. 89
Hamburger, H. L. 89 135
Hamiltonian matrix 75
Hardy, G. H. 136
Heinz, E. 134
Hermite normal form 34
Hermite normal form, reduction to 35
Hermite normal form, use in solving equations 35
Hermitely congruent matrices 84
Hermitian 62 164
Hermitian form 69
Hirsch, A. 140 172
Hirsch, K. A. 89
Hirsch’s theorems 140 141
Hodge, W. V. D. 89
Hoffman, A. J. 91 134 172
Hoffman, K. 90
Hohn, F. E. 90
Homogeneous function 103
Hua, L. K. 91 136
Hypercompanion matrix 52
Hyperplane 94
Identity matrix 2
Incidence matrix 18
INDEX 83 84
Index of imprimitivity 124 128
Index sets 9
Induced matrix 20
Inner product 60
Invariant factors 43
Inverse of a matrix 3
Irreducibility 56
Ising model 26
Jacobi matrices 166
Jacobson, N. 90
Jaeger, A. 90
Jordan normal form 54
Jung, H. W. E. 90
K nig, D. 136 nig, D. 136
Kantorovich Inequality 110 117
Kantorovich, L. V. 136
Kato 91
Khan, N. A. 136
Kotelyanski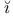 , D. 152 172 , D. 152 172
Kowalewski, G. 90
Kronecker delta 2
Kronecker product 8
Kronecker product, matrix product in terms of 9
Kuiper, N. H. 90
Kunze, R. 90
L vy — Desplanques theorem 145 146 vy — Desplanques theorem 145 146
L vy, L. 140 145 172 vy, L. 140 145 172
Lagrange identity 110
Laplace expansion theorem 14
Laplace expansion theorem, for permanents 20
Latent roots 23
Ledermann, W. 153 154 155 172
Ledermann’s theorem 153
Length of a vector 60
Lexicographic order 10
Lidski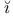 , V. C. 172 , V. C. 172
Line 94
Line segment 93
linear combination 28
Linear dependence 29
Linear equations 30
Linear equations, equivalent systems 33
Linear equations, homogeneous 31
Linear equations, inconsistent systems 35
Linear equations, nonhomogeneous 31
Linear equations, trivial solution to 31
Linear functional 101
Linear independence 29
Littlewood, J. E. 136
Lopes, L. 136
Lyapunov, A. 160 171
Lyapunov’s theorem 160
MacDuffee, C. C. 90 171
Marcus 91 135 136 137 172
Matrix 1
Maxfield, J. E. 137
Maximal root 124
McGregor, J. L. 136
Metzler, W. H. 90
Mine, H. 137 172
Minkowski determinant theorem 115
Minkowski inequality 109
Minkowski, H. 146 172
Mirsky, L. 90 136 137 172
Monic polynomial 40
Motzkin, T. S. 91
Moyls, B. N. 137 172
Muir 90
Multiplication of matrices 2
Multiplication of matrices, and vectors 3
Multiplication of matrices, by blocks 6
Multiplication of matrices, in terms of rows and columns 4
Murdoch, D. C. 90
Negative, definite 69
Negative, semidefinite 69
Neiss, F. 90
Nering, E. D. 90
Newman 91 135 137 149
Newton’s inequalities 106
Nilpotent matrix 5
Nilpotent matrix, example of 4
Nonderogatory 50
Nonnegative  -tuple 121 -tuple 121
Nonnegative (positive semidefinite) 69
Nonnegative matrix 121 152
Nonnegative orthant 95
Nonsingular matrix 3
Norm 40
Norm, Euclidean 18
Norm, of a vector 60
normal 62 161
Normal, real 63
Null space 31
Nullity 31
Orthogonal 63
Orthogonal, complex 63
Orthonormal 60
Orthostochastic 95
Ostrowski, A. 145 154 155 156 160 170 172 173
Ostrowski’s theorems 150 151 154
Ovals of Cassini 149
P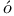 lya, G. 136 137 lya, G. 136 137
Paige, L. J. 90
Pairwise orthogonal 60
Parker, W. V. 90 144 148 173
Parker’s inequality 144
Parodi 171
Partitioned matrices 6
Pedoe, D. 89
Pencil of matrices 79
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -vector
-vector  -square matrix
-square matrix  th adjugate
th adjugate 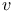 ,
,  )-matrix
)-matrix  z, A. R.
z, A. R. 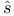 gorin discs
gorin discs  bner, W.
bner, W. 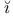 , D.
, D. 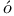 lya, G.
lya, G.