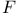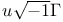|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Morimoto M. — Introduction to Sato's hyperfunctions |
|
|
 |
| Предметный указатель |
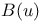 45 158 45 158
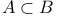 9 9
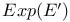 16 16
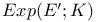 18 18
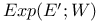 18 18
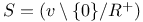 167 167
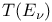 200 200
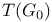 129 129
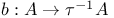 171 171
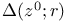 3 3
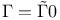 167 167
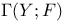 73 73
![$\Gamma[S;\mathscr{F}]$](/math_tex/fb2e6be064692607aa05b682d370ef9382.gif) 75 75
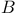 158 158
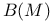 214 214
![$\mathfrak{B}[S]$](/math_tex/f776b871bd593fe3624b353b13a72ed182.gif) 45 159 45 159
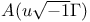 168 168
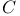 198 215 198 215
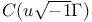 197 197
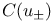 182 182
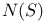 11 11
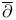 -resolution 114 -resolution 114
 -soft sheaf 95 -soft sheaf 95
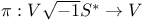 183 211 183 211
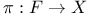 72 72
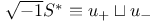 58 58
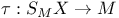 215 215
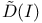 184 184
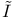 183 183
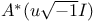 223 223
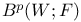 90 90
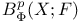 85 85
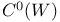 1 1
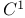 function 4 function 4
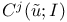 200 200
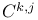 201 201
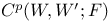 90 90
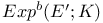 17 17
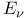 162 162
![${H}^{1}[A;\mathscr{O}]$](/math_tex/4b4d753e2729364decb3dd232e3c610a82.gif) 45 45
![${H}^{1}[K;\mathscr{O}]$](/math_tex/d6ac2cdfcb7b34f8b69ce37f7188609582.gif) 28 28
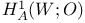 44 44
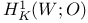 25 25
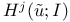 200 200
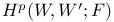 90 90
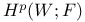 90 90
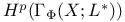 86 86
![${H}^{p}[S;\mathscr{F}]$](/math_tex/944bb1cc96ce7c75175648806e83d57482.gif) 88 88
![${H}^{p}[u,S;\mathscr{F}]$](/math_tex/d1fa707c1bfbf080254df4b458ee0d4c82.gif) 106 106
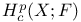 95 95
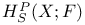 87 87
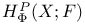 85 85
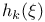 16 16
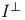 206 206
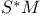 215 215
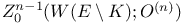 137 137
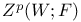 90 90
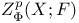 85 85
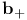 181 181
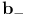 181 181
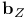 216 216
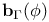 169 169
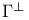 206 206
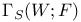 74 74
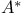 223 223
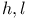 184 184
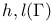 168 168
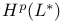 84 84
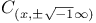 182 182
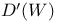 3 3
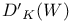 2 2
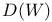 2 2
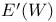 3 3
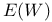 2 2
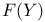 75 75
![${\mathscr{F}}[S]$](/math_tex/a75044d063c6d673a2c2242458172e1482.gif) 75 75
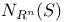 11 11
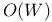 8 8
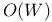 -convex hull 112 -convex hull 112
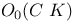 29 29
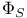 75 87 75 87
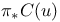 211 211
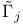 163 163
9-lemma 259 263
Analytic, cochain 207
Analytic, continuation 112
Analytic, functional 9
Annulus 24 132
Antipodal mapping 60
Ascoli-Arzel' theorem 9
B 215
Banach space 244
Bargman-Hall-Wightman theorem 235
Barrelled 244
Bochner tubular domain theorem 169
Bogolyubov theorem 216
Bornologique 244
Boundary operator 181
Boundary value, of holomorphic function 169
Boundary value, operator 169 216
Boundary values 46
Bounded 243
Canonical (n,0)-differential form 115
Canonical bilinear form 242
Canonical embedding 46
Canonical flabby resolution 84
Canonical mappings 245 246
Cauchy inequality 5
Cauchy integral, formula 4
Cauchy integral, theorem 4
Cauchy-Hilbert transform 28 142
Cauchy-Kovalevskaya theorem 232
Cauchy-Poincare theorem 131
Cauchy-Riemann, complex 114
Cauchy-Riemann, equations 4
Cauchy-Weil, integral formula 133
Cauchy-Weil, theorem 133
Cauchy-Weil, transform 138
Center of annulus 132
Characteristic function 55
Closed graph theorem 244
Coboundary 89
Coboundary operator 89
Cofinal 246
Cohomology group 85
Cohomology group, of complex 260 264
Cohomology group, with compact support 95
Compact mapping 249
Compatibility condition 48 80
Complete Reinhardt set 6
COMPLEX 260 264
Complex, neighborhood 11
Complex, of sheaves 84
Complexification 213
Cone 167
Conormal, space 227
Conormal, sphere bundle 183 215
Conormal, vector bundle 215
Constant presheaf 77
Convex hull 184
Convex hull, in sphere 168
Convex polyhedron 183
Convex set in sphere 168 183
Convex set in sphere bundle 216
Convolution 14
Cotangent, sphere bundle 215
Cotangent, vector bundle 215
Cylindric compact set 118
de Rham theorem 99
Decomposed singular support 220
| Decomposition to plane waves 229
Decreasing family 245
Decreasing family, of locally convex spaces 246
Decreasing sequence 245
Definite integral of hyperfunction 61 229
Denning function 45 161
Denning function, of analytic functional 28
Derived sheaf with support 99
Determined singular point 69
DFS space 254
Differential operator of infinite order 40 63
Dirac  -function 52 161 -function 52 161
Dirac measure 10
Direct image 211
Directed set 245
Distinguished boundary 3
distribution 3
Dolbeault theorem 115
Domain 6
Domain, of holomorphy 111
Dual, cone 184
Dual, set 206 216
Dual, space 242
Elliptic partial differential operator 234
Entire function of exponential type 16
Epstein theorem 217
Even hyperfunction 50
Everywhere singular 113
Exact 259 263
Exact sequence 259 263
Excision theorem 88
Exponential function 15
Extended tube 235
Family of supports 75
Finite part 54
First cohomology group, with compact support 35
First cohomology group, with support in close set 44
First cohomology group, with support in K 25
fl.dim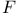 103 103
Flabby dimension 103
Flabby resolution 83
Flabby sheaf 81
Fourier-Borel transform 15
Fourier-Laplace transform 37
Frechet space 244
FS space 249
Fundamental theorem of microfunctions 207
Gauss kernel 67
Gelfand representation 15
General  -function 53 -function 53
Germ, of holomorphic functions 12
Germ, of presheaf 79
Germ, of real analytic functions 12
Grauert theorem 160
Hahn-Banach theorem 242
Hartogs theorem 5 112
Heaviside Y-function 54
Holomorphic, differential forms 114
Holomorphic, function 4
Holomorphic, function on 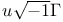 168 168
Holomorphic, functions over tangent sphere bundle 168
Holomorphic, parameter 55
Holomorphically convex 112
Homomorphism of complexes 260 264
Hyperfunction 45 158
Image 259 263
Increasing family 245
Increasing family, of locally convex spaces 246
Increasing sequence 245
Indefinite integral 51
Inductive limit 246
Inductive ordered set 81
Injective increasing sequence 251
Invariant under the Lorentz infinitesimal transformations 238
Jost point 236
Jost theorem 236
Kaneko theorem 70
Kashiwara theorem 218
Kernel 259 263
Laplace-Martineau transform 146
Leray theorem 93
LF space 252
Lie between 24 135
Linear functional 242
Linear topological space 241
Linearly convex 113
Liouville theorem 29
Local operator 63
Localization conditions 80
Locally, analytic functional 12
Locally, closed 11
Locally, convex 241
Locally, convex space 242
Logarithmically convex 8
Long Exact Sequence 85 88
Long exact sequence, of a cohomology groups of relative covering 91
Lorentz group 235
Lower semicontinuous 244
Mackey theorem 243
Mackey-Arens theorem 244
Malgrange theorem 115
Martineau Edge-of-the-Wedge theorem 218
Martineau-Harvey theorem 148
Maximal modulus principle 6
Mayer-Vietoris theorem 190
Meromorphic hyperfunction 53
Micro-analytic 58
Micro-analytic hyperfunction 221
Microfunction 182 198
Minkowski inner product 235
Mittag-Leffler theorem 32
Montel, space 244
Montel, theorem 6
Nonregularity 68
Norm 241
Normal sphere bundle 214
Normal vector bundle 214
Normed space 244
Odd hyperfunction 50
Oka theorem 14 115
Open neighborhood of locally closed set 11
Open polydisc 3
Open set, of convergence 7
Open set, of holomorphy 111
Osgood theorem 5
p-coboundary 90
p-cochain 89
P-cocycle 90
Paley-Wiener theorem 116
Paracompact space 95
Paracompactifying support 95
Patching condition 48 81
Plurisubharmonic function 113
Poincare lemma 98
Polar set 256
Polya theorem 21
Polydisc, (closed) 3
Polyhedron 141
Polynomially convex 14
Polynomially convex hull 14
Positive light cone 235
Presheaf 76
Presheaf, homomorphism 78
Presheaf, of arbitrary functions 78
Presheaf, of G-modules 77
Presheaf, of holomorphic functions 77
Presheaf, of hyperfunctions 77
Presheaf, of real analytic functions 77
Presheaf, of rings 77
Presheaf, of sections 79
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



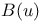
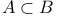
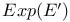
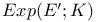
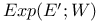
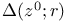
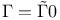
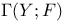
![$\Gamma[S;\mathscr{F}]$](/math_tex/fb2e6be064692607aa05b682d370ef9382.gif)
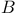
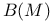
![$\mathfrak{B}[S]$](/math_tex/f776b871bd593fe3624b353b13a72ed182.gif)
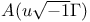
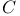
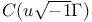
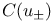
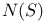
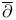 -resolution
-resolution  -soft sheaf
-soft sheaf 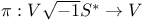
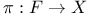
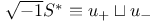
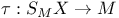
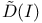
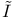
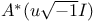
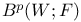
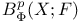
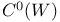
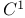 function
function 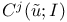
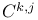
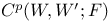
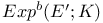
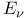
![${H}^{1}[A;\mathscr{O}]$](/math_tex/4b4d753e2729364decb3dd232e3c610a82.gif)
![${H}^{1}[K;\mathscr{O}]$](/math_tex/d6ac2cdfcb7b34f8b69ce37f7188609582.gif)
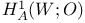
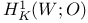
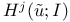
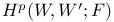
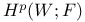
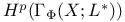
![${H}^{p}[S;\mathscr{F}]$](/math_tex/944bb1cc96ce7c75175648806e83d57482.gif)
![${H}^{p}[u,S;\mathscr{F}]$](/math_tex/d1fa707c1bfbf080254df4b458ee0d4c82.gif)
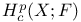
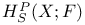
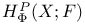
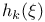
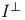
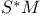
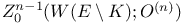
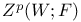
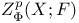
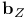
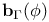
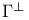
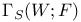
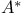
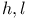
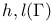
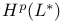
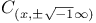
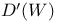
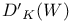
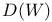
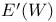
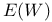
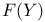
![${\mathscr{F}}[S]$](/math_tex/a75044d063c6d673a2c2242458172e1482.gif)
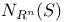
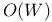
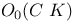
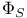
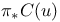
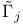
 -function
-function