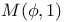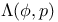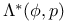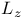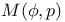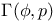|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lorentz G.G. — Bernstein Polynomials |
|
|
 |
| Предметный указатель |
"Admissible" lines 100
Absolutely monotone functions 87—88
Almost convergent sequences 38
Autonomous sets 108—114 120—121 123—124
Banach spaces 52—53
Bernstein polynomials 3—6
Bernstein polynomials of analytic functions 87—94 104—117 121—124
Bernstein polynomials of discontinuous functions 27—29
Bernstein polynomials of functions of bounded variation 23—25
Bernstein polynomials on the interval 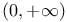 36—37 36—37
Bernstein polynomials, asymptotic formulae for 22—23 93—94 123
Bernstein polynomials, contour integrals for 92—94 123
Bernstein polynomials, degenerate 43—44 121—124
Bernstein polynomials, degree of approximation by 19—22
Bernstein polynomials, derivatives of 12—13 25—27
Bernstein polynomials, k-dimensional 51
Binomial probabilities 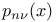 4 4
Binomial probabilities 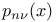 , estimates for 13—19 , estimates for 13—19
Binomial probabilities 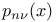 , generalized 45—46 , generalized 45—46
Compact sets 33—34 36
Complete spaces 52
Concave, relatively 68—70
Conjugate spaces 73 76—77
Convex functions 23
Degree of approximation 19—22 48—50
Divided differences 44—45
Dual spaces 76
Equimeasurable functions see "Rearrangements of functions"
Essential variation 23
Euler methods 41—43
Generalized 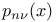 45—46 45—46
Generalized Bernstein polynomials 46—48 50—51
Generalized Bernstein polynomials for integrable functions 30—34
Generalized Bernstein polynomials for measurable functions 34—36
Hausdorff methods 81—86
Hoelder, inequality of 31
Inequalities for 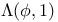 and and 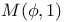 68 72 68 72
Inequalities for 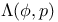 71—72 71—72
Level functions 70
Linear functionals 53—54 72—73
Linear functionals in space  57 57
Linear functionals in space C 55—56
Linear functionals in spaces 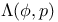 and and 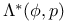 72—74 72—74
| Linear functionals, positive 56—57
Linear operators 32
Localization, theorems of 7 91—92
Loop 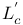 109—110 113—114 109—110 113—114
Loop 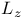 94—104 94—104
Measure-preserving transformations 60—61
Method of the steepest descent 106
Methods of summation 37—44 81—86 117—123
Metric means 34
Minkowski, inequality of 31
Modulus of continuity 19
Moment problems 54
Moment problems for spaces  , M, , M, 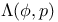 , , 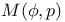 81 81
Moment problems for spaces X(C) 77—80
Moment problems for Stieltjes integrals 57—59
Muentz, theorem of 46
Newton's interpolation formula 45
Norm 52 54
Normal spaces 67 72
Perfect spaces 76—77
Polynomials with integral coefficients 6 48—50
probability 4 6 15
Rearrangements of functions 59—61 63—64
Rearrangements of functions, decreasing 60 63
Relation 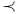 62 70 78 62 70 78
Riesz, inequality of 63—64
Separable spaces 52
Sets of convergence 107—110 114—115 119—123
Space  31—34 53 81 31—34 53 81
Space 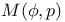 65 75—77 81 65 75—77 81
Space 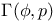 75—77 75—77
Space 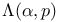 65—66 65—66
Space 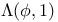 65 68 65 68
Space 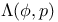 65 68—75 81 65 68—75 81
Space C 52—53 55—57
Space S 35—36
Space X(C) (Koethe — Toeplitz) 66—68 79—80
Star-shaped regions 101 118
Stieltjes integrals 54—55
Stone's theorems 9—12
Summability functions 39—41 43 84—86
Summation of power series 117—123
Uniform absolute continuity 79
Weierstrass, theorem of 5—9
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



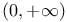
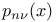
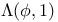 and
and