|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Young R.M. — An Introduction to Nonharmonic Fourier Series |
|
|
 |
| Предметный указатель |
Korobeinik, Ju.F. 221 222 226 227 229
Kothe, G. 208 229
Krein — Milman — Rutman theorem 39 209
Krein, M.G. 46 209 219 225 228 229 230
Krotov, V.G. 204 230
Kwapien, S. 204 230
l.i.m. see “Limit in mean”
Lagrange interpolation series 150—151 176 219
Laguerre's theorem 79
Landau's theorem 218
Landau, H.J. 218 230
Legendre polynomials 15
Legendre's duplication formula 79
Lerer, JL.E. 209 230
Levin, B.Ja. 210 219—222 230
Levinson's theorem, on completeness of exponentials in ![$C[-\pi D, \pi D]$](/math_tex/e736cc25045753dfaf7571926b8dc50882.gif) 117 216 117 216
Levinson's theorem, on completeness of exponentials in ![${L}^{p}[-\pi, \pi]$](/math_tex/fe4e5badcf95cc96a1eeb0e2a02fe21382.gif) 118 216 118 216
Levinson's theorem, on density and the completeness radius 138 218
Levinson's theorem, on equiconvergence of ordinary and non-harmonic Fourier series 224
Levinson's theorem, on exponentials close to the trigonometric system 119 122 216
Levinson, N. 90 111 143 210 213—218 224 230
Limit in mean 199
Lin, B. 209 230
Lindelof, E. 54 212 231
Lindenstrauss, J. 203 205 207 208 230
Linear operator see “Operator”
Linked 130
Littlewood, J.E. 158 220 229
Liusternik, L.A. 209 229
Lorch, E.R. 208 230
Lorentz, G.G. 205 230
Luxemburg, W.A.J. 213 230 231
Lyubarskii, J.L 220 222 230
Malliavin, P. 142 218 22(5
Marcinkiewicz, J. 204 231
Markushevich, A L 44 210 231
Marti, J.T. 203 204 231
Martirosjan, V.M. 222 231
Maximum modulus function 62
Maximum principle 62 80 95 96 174
Mean-value formula, for analytic functions 17
Mean-value formula, for harmonic functions 59
Measurable sequence 138
Meletidi, M.A. 206 209 228 231
Miintz, C.H. 205 213 231
Milman, D.P. 209 230
Minimal 28 130
Minimum modulus 211 212
Mittag — Leffler function 68
moment 21 146 219
Moment problem 146—153 219
Moment problem, relation to bases 169—171 222
Moment sequence 146 186
Moment space 146 154 169
Moment space, and equivalent sequences 167—170
Moment space, of a Riesz basis 148
Morris, P. 205 227
Muckenhoupt condition 223
Muentz's Theorem 91 93 213
Natanson, LP. 219 257
Natural basis 2 3 7
Nehari, Z. 207 231
Neuwirth, J.H. 209 228
Neville, C.W. 220 231
Nonharmonic Fourier frame 185
Nonharmonic Fourier series 42 209 221
Nonharmonic Fourier series, equiconvergence with ordinary Fourier series 197—201
Nonharmonic Fourier series, pointwise convergence 197—201
Normal basis 26 207
Nudelman, A.A. 219 230
O'Hara, P.J. 213 257
Onto mapping 182
Open mapping theorem 30 188
Operator of finite rank 41
Operator, bounded from below 36 157 186
Operator, compact 40 41 45
Operator, Hilbert — Schmidt 45 51
Operator, of finite rank 41
Operator, positive 34 48
Operator, square root of 34
Order 62—68
Order, formula for 64
Order, in terms of Taylor coefficients 67
Order, of a canonical product 69
Order, of a derivative 67
Order, of a product 67
Orlicz's theorem 208
Orlicz, W. 208 231
Orthogonal 13 206
Orthogonal polynomials 206
Orthogonal system 26
Orthonormal basis 6
Orthonormal basis, for  11 11
Orthonormal basis, for 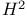 10 10
Orthonormal basis, for 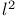 7 7
Orthonormal basis, for ![${L}^{2}[-\pi, \pi]$](/math_tex/c9bbcf78b83f908b5a56bf979ea7c2a282.gif) 7 7
Orthonormal basis, for ![${L}^{2}[0, \pi]$](/math_tex/f80babed03d7f77b515da5f2d570eb4f82.gif) 14 14
Orthonormal basis, for P 106
Orthonormal basis, stability of see “Stability”
Orthonormal sequence 14 15
Oskolkov, V. 222 231
Ostrovskii, I.V. 230
Paley — Wiener space 19 105—109 112 126 149 215
Paley — Wiener stability criterion 38 42 48 209
Paley — Wiener theorem, on finite Fourier transforms 100—105 214
Paley — Wiener theorem, on minimal sets of complex exponentials 130 217
Paley — Wiener theorem, on stability of bases 38 41 209
Paley, R.E.A.C 38 42 111 139 206 209 213—217 219—221 223 257
Parseval's identity 6 9 12 106
Parseval's identity, generalized 7
Partial sum operator 24
Partial sum operator, adjoint of 27
Pavlov, B.S. 223 231
Pelczynski — Singer theorem 208
Pelczynski, A. 203—205 208 226 230 231
Perturbation of a basis see “Stability”
Peterson, D.R. 218 257
Phragmen — Lindeloef method 80—87
Phragmen — Lindeloef theorem 80 212
Phragmen, E. 212 257
Plancherel — Polya theorem, on an inequality for functions in 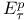 93 214 93 214
Plancherel — Polya theorem, on differentiation in 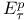 99 214 99 214
Plancherel's Theorem 100 106 195
Plancherel, M. 94 212 214 257
Point-evaluation functional 16
Pointwise convergence, of Fourier series 9 197 201
Pointwise convergence, of nonharmonic Fourier series 197—201
Poisson summation formula 105
Polar decomposition 48
Pollard, H. 207 215 226 231
Polya maximum density 138 143
Positive matrix 19
Positive operator 34 48
POVZNER, A. 232
Powers, completeness of 21 22
Primary factors 55
Property SAIN 205
Quadratic form 157 159
Quadratically close 45 46 51
Rahman, Q.l. 213 228
Redheffer's theorem 137 218
Redheffer, R.M. 212 215—218 225 232
Reflexive Banach space 28 204
Reproducing kernel 15—19 206
Reproducing kernel, Bergman kernel 18
Reproducing kernel, for P 107
Reproducing kernel, Szegoe kernel 16 158
| Retherford, J.R. 209 210 232
Riemann — Lebesgue lemma 200
Riesz (F.and M.) theorem 215
Riesz basis 30—37 169 188 208 221
Riesz basis, of complex exponentials 42 148 151 170—177 181 191 192 196—201
Riesz representation theorem 20 53 91 152
Riesz — Fischer sequence 146 153—161 180 220
Riesz — Fischer sequence, of complex exponentials 162—166
Riesz — Fischer theorem 7
Riesz, F. 34 48 206 210 220 228 232
Rogers, C.A. 204 228
Rosenbaum, J.T. 220 232
Rosenthal, H.P. 207 229
Rota, G.C 210 226
Royden, H.L. 205 232
Ruckle, W.H. 209 232
Rudin, W. 94 97 205 213—215 232
Russell, D.L. 210 252
Rutman, M.A. 209 230
Sampling theorem 107
Schaeffer, A.C 212—214 222—224 227
Schaefke, F.W. 210 232
Schafke's theorem 50 210
Schauder basis 1 207
Schauder's system 3 204
Schauder's theorem 4
Schauder, J. 1 206 252
Schmeisser, G. 213 228
Schonefeld, S. 204 232
Schur's lemma 159
Schwartz, J.T. 206 219 220 227
Schwartz, L. 139 213 215 217 218 232
Sedleckii's theorem, on equiconvergence of ordinary and non-harmonic Fourier series 223
Sedleckii's theorem, on Fourier — Stieltjes transforms 177 222
Sedleckii, A.M. 217 218 220—224 232 233
Self-adjoint operator 186 189
Self-adjoint operator, formula for norm 48
Sengupta, A. 210 233
Separable 2 6
Separated sequence 98 179—181 184 221
Sequence,  -independent 40 46 -independent 40 46
Sequence, Bessel see “Bessel sequence”
Sequence, closed see “Complete sequence”
Sequence, complete see “Complete sequence”
Sequence, density of see “Density”
Sequence, equivalent sequences 167 170
Sequence, free 28
Sequence, fundamental see “Complete sequence”
Sequence, independent 28
Sequence, interpolating see “Interpolating sequence”
Sequence, measurable 138
Sequence, minimal 28 130
Sequence, quadratically close sequences 45 46 51
Sequence, Riesz — Fischer see “Riesz — Fischer sequence”
Sequence, separated 98 179—181 184 221
Sequence, symmetric 139 148 151
Sequence, total see “Complete sequence”
Sequence, uniform density 1 212 214
Sequence, uniformly minimal 160
Set of uniqueness 112 174
Shah, S.M. 211 233
Shannon's sampling theorem 107
Shannon, C.E. 107 233
Shapiro, H.S. 160 206 213 220 233
Shields, A.L 160 220 255
Shisha 0. 215 257
Shohat, J.A. 219 255
Simon, P. 204 208 227
Sine type, function of 171—174 224
Sine type, function of, zeros of 173 174
Singer, I. 203 205 208 209 221 230 231 233
Sjoelin, P. 204 208 227
Square root, of an operator 34
Stability, of bases in Banach spaces 37—41 209
Stability, of complete sequences in Banach spaces 209
Stability, of complete sequences of complex exponentials 131—137 217 218
Stability, of frames 191—196
Stability, of interpolating sequences 179—184
Stability, of nonharmonic Fourier series 190—197
Stability, of orthonormal bases in Hilbert space 41—51
Stability, of Riesz bases of complex exponentials 190—197
Stability, of the trigonometric system 42—44 118—122 216
Stepanoff, W. 206 233
Stieltjes, T.J. 219 233
Stray, A. 222 233
Sturm — Liouville series 47 210
Sturm — Liouville system 46
Subharmonic function 94 95
Summability 201
Svedenko, S.V. 220 233
Symmetric sequence 139 148 151
Sz.-Nagy, B. 34 48 206 210 232
Szasz, O. 201 213 216 233
Szego, G. 16 206 212 213 257 233
Szegoe kernel 16 158
Talaljan, F.A. 233
Tamarkin, J.D. 219 233
Taylor, A.E. 36 186 233
Taylor, B.A. 220 233
Titchmarsh, E.C 75 83 206 210—212 214 220 233
Total sequence see “Complete sequence”
Trigonometric moment problem 145 170 219
Trigonometric moment problem, generalized 148
Trigonometric polynomial, approximation by 8
Trigonometric polynomial, inequality for 86
Trigonometric system 7 8 20 112—117 203
Trigonometric system, completeness of 8 20
Trigonometric system, stability of 42—44 118—122 196 216 218 223 224
Turku, H. 220 233
TYPE 71
Tzafriri, L. 203 207 208 230
Unconditional basis 3 13 204
Unconditionally convergent series 2 204
Uniform approximation 3 129
Uniformly minimal 160
Uniqueness, of an entire function 90—92 105 107 108 111 216
Unitary operator 48
Upper density 138 143
Valiron, G. 210 233
Verblunsky, S. 224 233
Vitali's theorem 14 206
Vitali, G. 206 234
Wallen, L.J. 210 234
Wallis's product 58
Walsh, J.L. 205 207 223 234
Weak basis 203
Weak convergence 136
Weaver, W. 107 233
Weierstrass primary factors 55
Weierstrass's approximation theorem 3 8 21 113 205
Weierstrass's approximation theorem, generalizations of 205
Weierstrass's factorization theorem 54 55 211
Weierstrass, K. 54.205 211 234
Weighted interpolation 158
Whittaker, E T. 107 234
Whittaker, J.M. 215 234
Wiener, N. 38 42 111 139 206 209 213—217 219—221 223 25/
Williams, D.L. 220 228 233
Wolibner's theorem 205
Wolibner, W. 205 234
Young, R.M. 215 218—223 234
Zaharjuta, V.P. 222 227
Zeros, of an entire function, and growth 59—62 64—66 69—73 75 85—93
Zeros, of an entire function, density of 90 213
Zeros, of an entire function, functions of nonintegral order 75 76
Zeros, of an entire function, real 79
Zippin, M. 207 208 229 230
Zygmund, A. 206 234
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



![$C[-\pi D, \pi D]$](/math_tex/e736cc25045753dfaf7571926b8dc50882.gif)
![${L}^{p}[-\pi, \pi]$](/math_tex/fe4e5badcf95cc96a1eeb0e2a02fe21382.gif)

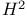
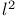
![${L}^{2}[-\pi, \pi]$](/math_tex/c9bbcf78b83f908b5a56bf979ea7c2a282.gif)
![${L}^{2}[0, \pi]$](/math_tex/f80babed03d7f77b515da5f2d570eb4f82.gif)
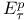
 -independent
-independent