Авторизация
Поиск по указателям
Bouc S. — Green Functors And G-Sets
Обсудите книгу на научном форуме Нашли опечатку?
Название: Green Functors And G-SetsАвтор: Bouc S. Аннотация: This book provides a definition of Green functors for a finite group G, and of modules over it, in terms of the category of finite G-sets. Some classical constructions, such as the associated categroy or algebra, have a natural interpretation in that framework. Many notions of ring theory can be extended to Green functors (opposite Green functor, bimodules, Morita theory, simple modules, centres, ...). There are moreover connections between Green functors for different groups, given by functors associated to bisets. Intended for researchers and students in representation theory of finite groups it requires only basic algebra and category theory, though knowledge of the classical examples of Mackey functors is probably preferable.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1997Количество страниц: 342Добавлена в каталог: 02.12.2009Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
181 46 47 76 81 72 65 278 127 115 125 143 143 296 296 68 308 71 53 47 183 97 183 183 275 7 168 146 8 130 72 194 237 256 183 183 206 206 282 275 193 193 242 14 16 167 171 308 185 276 310 218 218 230 199 50 186 9 145 11 15 23 316 29 193 196 188 207 209 205 335 188 185 84 218 112 273 278 308 307 199 313 168 171 127 181 273 134 171 232 194 315 316 231 A-mod 48 a.m 49 Adjunction between 38 Adjunction between 148 Adjunction, co-unit 185 Adjunction, unit 185 Algebra associated to a Green functor 84 99 164 Alperin’s conjecture 304 B 52 Balanced 99 154 Bifunctoriality 46 47 Bimodule 141 Bimodule construction 153 Bimodule, structure on 142 Biproducts 68 Biset 167 Biset, composition with 168 Blocks of Mackey algebra 335 Burnside functor as Green functor 55 Burnside functor as initial object 57 Burnside functor as Mackey functor 52 Burnside functor as unit 59 Cartesian product in 109 Cartesian product in 103 Category 186 Category, adding direct summands to a 310 Category, associated to a Green functor 67 Category, equivalence of 79 310—312 314 Category, representation of 71 81 Centre 305 Centre of Yoshida algebra 335 Coinduction 180 Coinflation 168 217 Commutant 143 Commutative Green functor 110 129 305 Commute 136 Composition and associated categories 173 Composition and Green functors 170 Composition and modules 175 Composition and tensor product 168 Composition with a biset 168 Direct summand in 82 Divides in 82 Dual of a module 130 Embedding of algebras 112 Endosimple A-module 304 Equivalence of categories 79 84 112 129 141 155 310—312 314 Equivalence of the definitions of Green functors 48 Examples of algebras 94 95 Examples of composition with a biset 168 Examples of Frobenius morphisms 227 Examples of functors 215 Examples of functors 332 Examples of Green functors 264 Finitely generated module over a Green functor 114 Frobenius morphisms 223 Functor from G-sets to 68 Functor of evaluation 81 Functorial ideal 291 Functoriality of 147 Functoriality of 177 Functoriality of 24 Functoriality of 146 G.s.t 229 Generators and relations for 85 88 Generators and relations for the Mackey algebra 7 Green functors and solvable 314 Green functors, centre 305 Green functors, composition with a biset 170 Green functors, definition in terms of G-sets 46 Green functors, definition in terms of subgroups 41 Green functors, direct sum 305 Green functors, tensor product 134 G\U.Y 183 Identification of 145 Identification of 320 323 327 Injective on the orbits 177 186 192 Left adjoint and Morita contexts 273 Left adjoint and tensor product 272 Left adjoint to 197 Left adjoint to 183 Lindner construction 94 Mackey algebra 7 Mackey algebra, anti-automorphism 10 Mackey axiom 5 Mackey functors, composition with a biset 168 Mackey functors, definition as modules 7 Mackey functors, definition in terms of G-sets 6 Mackey functors, definition in terms of subgroups 5 Mackey functors, internal homomorphisms 9 Mackey functors, tensor product of 9 Module of finite type 114 Module over a Green functor 41 47 Module over a Green functor, examples 61 Module over the Burnside functor 59 Module, dual 130 Module, right 129 Morita context 100 154 Morita equivalence 99 Morita equivalence of algebras 99 100 Morita Theory 155 160 Morphism of bimodules 141 Morphism of Green functor 41 Morphism of mackey functors 5 6 Morphism of modules over a Green functor 42 Morphism, bilinear 37 127 Morphism, Frobenius 223 Morphism, n-linear 29 Morphism, universal property 29 Multiple of, in CA 82 Natural transformation 316 Non-commutative tensor product 164 Opposite Green functor 127 Product 167 Product 125 Product 134 Product 123 Product 231 Product 317 Progenerator 115 117 118 155 161 321 Projective G-algebra 292 Projective relative to 102 Projective relative to, solvable 314 q(L) 183 Relative projectivity 100 Representation of a category 71 81 Residual rings 274 Restriction 5 Restriction for 15 23 Restriction for 10 Right adjoint to 210 Right modules 129 S.T 229 Same stabilizers 100 Simple Green functors 291 Simple Green functors, classification 295 simple modules 275 Simple modules, classification 276 Simple modules, structure 282 Source algebra 114 Surjective Morita context 154 Tensor product and composition with a biset 168 Tensor product and left adjoints 227 Tensor product and residues 298 Tensor product and right adjoints 242 Tensor product of "algebras" over 164 Tensor product of Green functors 134 Tensor product of Green functors, universal property 137 Tensor product of modules over Green functors 140 Tensor product of simple modules 298 Tensor product, associativity 38 Tensor product, commutativity 38 Tensor product, n-fold 25 Tensor product, n-fold, universal property 29 Thevenaz’s theorem 295 Trace see "Transfer" TRANSFER 5 Transfer for 15 23 Transfer for 10 U.Y 183 Unitary Green functor 46 Unitary morphism of Green functors 41 43 U[X] 173 Yoshida algebra 95 Yoshida algebra, centre 335 Z(A) 305
Реклама
 |
|
О проекте
|
|
О проекте



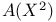
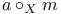
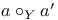
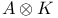
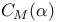
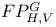
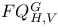
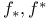
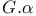
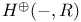
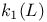
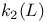
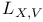
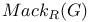
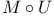
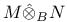
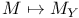
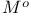
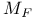
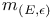
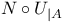
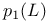
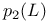
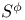
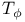
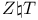
![$[m\otimes n]_K$](/math_tex/91fbb16811ec244ab5f2ec9fa582597682.gif)
![$[m\otimes n]_{(Y, \phi)}$](/math_tex/fd0b99e644dc005b274ce51e07b5573882.gif)
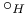
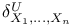
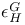
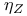
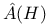
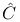
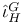
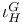
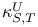
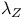
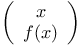
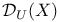
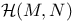
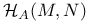
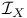
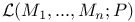
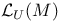
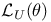
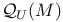
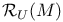
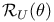
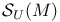
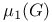
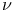 -disjoint
-disjoint 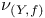

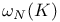
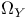
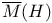
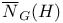
 -perfect
-perfect 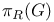
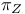
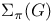
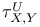
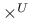
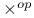
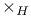
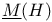
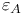
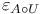
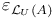
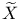
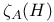
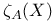
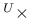
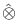 and
and 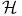
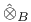 and
and 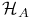
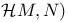
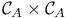
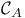
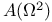
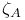
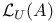
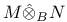
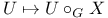
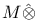
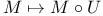
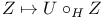
 for
for