|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Tignol J.-P. — Galois' Theory of Algebraic Equations |
|
|
 |
| Предметный указатель |
Abel, Niels-Henrik 210-212
Abelian group 242
Abel’s condition 231-232 242-243 293-294
Abel’s theorem on natural irrationalities 219-225
al-Khowarizmi, Mohammed ibn Musa 9-11 22
Alembeit, Jean Le Rond d’ 115
Alternating group 228 276
Ap ry, Roger 112 ry, Roger 112
Arabic algebra 9-12 22
Artin, Emil 305-306 309
Babylonian algebra 2-5 7 22
Bachet de M ziriac, Claude 87 ziriac, Claude 87
Bernoulli, Jacques 110
Bernoulli, Nicholas 75
Bezout’s elimination theory 69
Bezout’s method 123-126 134-137
Bezout’s Theorem 87
Bolzano, Bernhard 121
Bombelli, Rafaele 20 26
Bourbaki, Nicolas 306
Cardano, Girolamo 13-15 21-22 25-26 40
Cardano’s Formula 15-20 78 128-132 277
Casus irreducibilis 19 109
Cauchy, Augustin-Louis 117 210-212 228
Common root of two polynomials 56
Complete solvability (by radicals) 264
Congruence (modulo an integer) 168
Constructible point 201
Coset 141 255
Cotes — de Moivre formula 73 76-81 83 94-95
Cotes, Roger 75-77
Cubic equation 13-20 61-63 70-71 109 125-126 128-134 156 277
Cyclic group 89
Cyclotomic equation 98 209 241 276 292;see
Cyclotomic polynomial (or equation) 90-92 231
Cyclotomy 83
De Moivre’s Formula 42;see Cotes-de Moivre formula monic polynomial
Dedekind, Richard 196 305 309
Degree (of a field extension) 307
Delambre, Jean-Baptiste 209
Derivative (of a polynomial) 53
Descartes, Ren 22 28-30 37 22 28-30 37
Descartes’ method for quartic equations 64-65
Diophantus of Alexandria 8 29
Discriminant 106 112-114 276-278 292
Eisenstein, Ferdinand Gotthold Max 176
Elementary symmetric polynomial 99
Elimination theory 56 68 88 124
Equation of squared differences 113
Euclid 5-8 11 22
Euclidean division property 43 87
Euclid’s algorithm 27 44
Euler, Leonhard 56 73 80 96 110 115 171 205 206
Euler’s method of a root of unity 86;see Bezout’s method exponent
Euler’s method of an element in a group 174;see Bezout’s method exponent
Euler’s method of an integer modulo a prime 172;see Bezout’s method exponent
Expression (solution) by radicals 213 264
Fermat prime 205
Fermat’s theorem 171 174 206
Ferraii’s method 22-24 134-135 262 277-278
Ferrari, Ludovico 21
Ferro, Scipione del 13
Fior, Antonio Maria 13
Foncenex, Daviet Francois de 116
Fourier, Jean-Baptiste Joseph 232
Fundamental theorem of algebra 36 74 80 104 115-122
Fundamental Theorem of Galois Theory 142 307-316
Fundamental theorem of symmetric fractions or polynomials 99-106
Galois extension (of fields) 307
Galois group 241-242
Galois group of a field extension 307
Galois group of a polynomial 237
Galois resolvent 236 245
Galois, 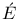 variste 232-234 236 240 264 298 variste 232-234 236 240 264 298
Gandz, Solomon 5
Gauss on cyclotomic equations 175-196 231
Gauss on number theory 168-175
Gauss on regular polygons 206
Gauss on the fundamental theorem of algebra 104 105 116 121 210
| Gauss, Carl Friedrich 167
Girard, Albert 28 35-38 65
Girard’s theorem 35 116
greatest common divisor (GCD) 44
Greek algebra 5-9 21
Group early results 138-142 157 228
Group of arrangement 296
Group of substitutions 296
Height (of a radical extension) 213
Hero 8
Hippasus of Metapontum 6
Hudde, Johann 53
Ideal (in a commutative ring) 117
Index (of a subgroup) 142 266
Irreducibility 175-178 188 196-200
Irreducible polynomial 48
Isotropy group 139 282
Jacobson, Nathan 306
Khayyam, Omar 11
Kieman, Melvin 305
Knon, Wilbur Richard 6
Kronecker, Leopold 48 117 196 219 305
Lacroix, Sylvestre-Franfois 209
Lagrange resolvent 138 146-150 156 193 196 271
Lagrange, Joseph-Louis 100 116 126-146 153 209 285
Landau, Edmund 175
Leading coefficient 42
Lebesgue, Henri 153 164
Legendre, Adrien-Marie 209
Leibniz, Gottfried Wilhelm 67 74-75 92-93 110
Liouville, Joseph 233
Mertens, Franz 175
Minimum polynomial 181 236
Moivre, Abraham de 77-81 83 84 115 123 158
Multiple root 51 108
Newton, Isaac 38 74 75 93-94
Newton’s Formulas 38-39 110
Normal subgroup 255
Novy, Lubos 305
Nunes, Pedro 26 37
Orbit 279 281
Order of a group 139
Order of an element in a group 174
Pacioli, Luca 12
Period (of a cyclotomic equation) 184
Primitive root of a prime number 169
Primitive root of unity 86
Pythagoras 6
Quadratic equation 1-11
Quartic equation 21-24 64-65 126 134-135 156-157 262-264 277-278
Quotient ring (by an ideal) 117
Radical field extension 213
Rational equation 65-66
Rational root 65
Recorde, Robert 26
Regular polygon 83 167 200-206
Resolvent cubic equation 24 262-264 277
Resultant 56 69 96 113
Root of a complex number 80 81
Root of a polynomial 51
Root of unity 82
Ruffini, Paolo 209-212 219 225
Ruler and compass constructions 167 200-206 232
Schur, Issai 175
Solvability by radicals 83 158-164 192-196
Solvable group 265 294
Stevin, Simon 1 26-28 40
Symmetric group S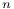 138 138
Symmetric polynomial (or rational fraction) 99
Tartaglia 13-15 Fontana Niccolo
Transitive (group of permutations) 279
Tschimhaus, Ehrenfried Walter 67-68
Tschimhaus’ method 68-71 132-134
van der Waerden, Bartel Leendert 305
van Roomen, Adriaan 30-34;see Romanus Adrianus
Vandermonde, Alexandre-Th ophile 100 153-164 182 ophile 100 153-164 182
Vi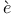 te, Fran te, Fran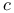 ois 1 29 32-35 40 61-63 ois 1 29 32-35 40 61-63
Wantzel, Pierre Laurent 204 212 225
Waring, Edward 100-103 126
Weil, Andre 5 304
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ry, Roger
ry, Roger 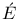 variste
variste 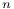
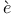 te, Fran
te, Fran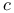 ois
ois