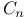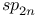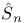|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Collingwood D.H., McGovern W.M. — Nilpotent Orbits in Semisimple Lie Algebras |
|
|
 |
| Предметный указатель |
Adjoint group 8
Adjoint orbit 9
Adjoint orbit, as a homogeneous space 10
Adjoint orbit, as a sympletic manifold 17
Adjoint representation 1
Annihilator in polynomial ring 3
Annihilator in the enveloping algebra 171
Associated variety 171
Automorphism group 7
Bala - Carter classification 124
Bala - Carter Theory 119
Borel subalgebra 32
Cartan decomposition 136
Cartan involution 136
Cartan subalgebra 19 120
Cayley triples 145
centralizer 10
Centralizer, classical component groups 88
Centralizer, component group 87
Centralizer, component groups 88
Centralizer, of a nilpotent element 49
Centralizer, of a semisimple element 20
Characteristic cycle 175
Classical algebras 11
Classical groups 10
Classification, Bala - Carter 124
Classification, classical cases 69
Classification, classical real nilpotent orbits 139
Classification, exceptional nilpotent orbits 127
Classification, nilpotent orbits 37
Classification, primitive ideals 173
Classification, real forms 135
Classification, semisimple orbits 25
Classification, strategy 32
Coadjoint orbit 11
Collapse operation 99
Conjugacy class 9
Conjugacy theorem, Cayley triples 145
Conjugacy theorem, Kostant 36 42
Conjugacy theorem, Mal'cev 36 43
Conjugacy theorem, minimal Levi subalgebras 120
Conjugacy theorem, normal triples 145
Conjugacy theorem, Rao 146
Conjugacy theorem, real standard triples 138
Diagonalizable operator 1
Distinguished nilpotent elements 121
Distinguished nilpotent orbits 121
Distinguished nilpotent orbits, classical cases 126
Distinguished nilpotent orbits, even 122
Distinguished parabolic subalgebra 123
Distinguished parabolic subalgebra, as Jacobson - Morozov 124
Distinguished semisimple orbits 29
Dixmier algebras 177
Dominant 45
Duflo's Theorem 172
Even nilpotent orbit 53 85 122
Even nilpotent orbit, Richardson 110
Exceptional cases 127
Exceptional cases, dimension 127
Exceptional cases, fundamental group 127
Exceptional cases, real 150
Exceptional cases, special 127
Exceptional cases, weighted Dynkin diagrams 127
Expansion operation 101
Exponents of a semisimple group 64
Finiteness Theorem, complex nilpotent orbits 46
Finiteness Theorem, real nilpotent orbits 150
Fundamental group 87
Fundamental group, any orbit 93
Fundamental group, equivariant 88
Fundamental group, exceptional cases 91 92
Generalized eigenspace decomposition 3
generic elements 21
Goldie rank polynomial 173
Harish - Chandra module 174
Hasse diagram 93
Hasse diagram, classical cases 93
Hasse diagram, duality map 102
Hasse diagram, exceptional cases 103
Hasse diagram, order reversing map 100
Hermitian form 140
Induced nilpotent orbit 106
Induced nilpotent orbit, 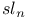 112 112
Induced nilpotent orbit, diagram in classical cases 116
Induced nilpotent orbit, dimension 108
Induced nilpotent orbit, independence of 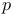 107 107
Induced nilpotent orbit, induction in stages 108
Induced nilpotent orbit, meeting a Levi subalgebra 127
Induced nilpotent orbit, partition in 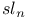 113 113
Induced nilpotent orbit, partition in classical cases 116
Induced nilpotent orbit, weighted Dynkin diagram 109
Irreducibility theorem 172
Isometry group 70
Isotropic submanifold 16
Jacobson - Morozov Theorem 36-37 137
Jordan block 31
Jordan decomposition theorem 2
Killing form 11
Left cell representation 174
Metaplectic representation 109
Minimal Levi subalgebras 120
Minimal nilpotent orbit 55 61
Minimal nilpotent orbit, partition 85
Minimal nilpotent orbit, rigid 109
Minimal nilpotent orbit, when even 85
Neutral element 33
Nilnegative element 33
Nilpositive element 33
Nilpotent cone 68
Nilpotent cone, as an irreducible variety 68
Nilpotent distinguished elements 121
Nilpotent element 2
Nilpotent in 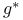 13 13
Nilpotent operator 1
Nilpotent orbit 9
Nilpotent orbits in 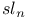 32 32
Nilpotent orbits, classical fundamental groups 91
Nilpotent orbits, dimension 90
Nilpotent orbits, dimension in 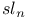 112 112
Nilpotent orbits, distinguished 121
Nilpotent orbits, exceptional cases 127
Nilpotent orbits, exceptional fundamental groups 92
Nilpotent orbits, exceptional real orbits 150
Nilpotent orbits, fundamental group 87
| Nilpotent orbits, Hasse diagram 55
Nilpotent orbits, in 70
Nilpotent orbits, in 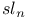 69 69
Nilpotent orbits, in 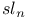 ( ( ) 140 ) 140
Nilpotent orbits, in 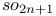 69 69
Nilpotent orbits, in 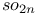 141 141
Nilpotent orbits, in 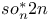 141 141
Nilpotent orbits, in 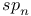 70 70
Nilpotent orbits, in 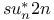 140 140
Nilpotent orbits, in 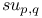 140 140
Nilpotent orbits, induced 106
Nilpotent orbits, ordering 95
Nilpotent orbits, partial ordering 55
Nilpotent orbits, Richardson 106
Nilpotent orbits, rigid 109
Nilpotent orbits, special 100
Nilpotent orbits, topology 87
Nilradical 32
Normal triple 145
Orbit, adjoint 9
Orbit, nilpotent 9
Orbit, semisimple 9
Parabolic subalgebra 51
Parabolic subalgebra, distinguished 123
Parabolic subalgebra, Jacobson - Morozov 52
Parabolic subalgebra, partition 111
Partition 30
Partition, collapse 99
Partition, expansion 101
Partition, for minimal orbit 85
Partition, for principal orbit 85
Partition, for subregular orbit 85
Partition, ordering 93
Partition, parabolic subalgebra 111
Partition, special 100
Partition, transpose 65 98
Partition, very even 70
Poincar - Birkhoff - Witt 171 - Birkhoff - Witt 171
Primitive ideal 171
Principal nilpotent orbit 46 55-56
Principal nilpotent orbit, partition 85
Principal nilpotent orbit, when even 85
Real forms 135
Real nilpotent orbits 139
Real nilpotent orbits, classical cases 139
Real nilpotent orbits, in 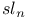 140 140
Real nilpotent orbits, in 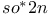 141 141
Real nilpotent orbits, in 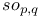 141 141
Real nilpotent orbits, in 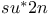 140 140
Real nilpotent orbits, in 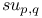 140 140
Real simple Lie algebras 135
Reductive 4
Regular semisimple 21
Regular semisimple element 21
Regular subalgebra 119
Representations of 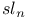 34 34
Richardson orbit 106
Richardson orbit, 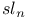 112 112
Richardson orbit, even 110
Richardson orbit, subregular orbit 110
Rigid nilpotent orbit 109
Rigid nilpotent orbit, 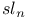 112 112
Rigid nilpotent orbit, classical cases 116-117
Root space decomposition 20
Sekiguchi's bijection 147
Semisimple element 2
Semisimple in 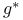 13 13
Semisimple operator 1
Semisimple orbit 9
Semisimple regular 21
Sign representation 166
Signature of a form 140
Signed Young diagram 140
Skew - Hermitian form 140
Spaltenstein map 100
Special nilpotent orbit 100
Special nilpotent orbit, duality 102
Special partition 100
Spectral decomposition 3
Springer correspondence 165 169
Springer correspondence, type 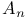 166 166
Springer correspondence, type 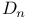 168 168
Springer correspondence, types 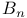 and and 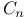 166 166
Standard triple 33
Standard triple, neutral element 33
Standard triple, nilnegative element 33
Standard triple, nilpositive element 33
Standard triples in 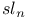 35 76 35 76
Standard triples in 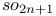 78 78
Standard triples in 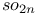 79 79
Standard triples in 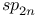 77 77
Standard triples, Cayley 145
Standard triples, normal 145
Subregular nilpotent orbit 55 59
Subregular nilpotent orbit, partition 85
Subregular nilpotent orbit, Richardson 110
Subregular nilpotent orbit, when even 85
symbols 166
Symmetric form 140
Symplectic form 140
Symplectic manifold 16
Symplectic vector space 15
Toral subalgebra 120
Transpose partition 65 98
Very even partition 70
Weighted Dynkin diagram 29 37 46
Weighted Dynkin diagram, exceptional cases 127
Weighted Dynkin diagram, exceptional real orbits 150
Weighted Dynkin diagram, in 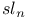 47 47
Weighted Dynkin diagram, in 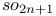 82 82
Weighted Dynkin diagram, in 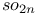 83 83
Weighted Dynkin diagram, in 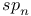 81 81
Weighted Dynkin diagram, induced orbit 109
Weighted Dynkin diagram, real cases 148
Weyl group 25
Weyl group representation symbols 166
Weyl group representations, 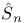 166 166
Weyl group representations, left cell 174
Weyl group representations, type 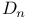 168 168
Weyl group representations, types 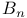 and and 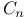 166 166
Young diagram 65
Young diagram, signature 140
Young diagram, signed 140
Young tableau 166
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



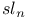
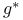
 )
) 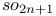
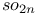
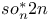
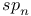
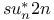
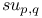
 - Birkhoff - Witt
- Birkhoff - Witt 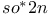
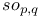
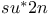
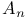
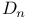
 and
and