|
Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета |
| Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск |
|
|
© Электронная библиотека попечительского совета мехмата МГУ, 2004-2025 |
|
О проекте |
|
О проекте
|


 of bivariate generalised Hermite polynomials of degree n is invariant under rotations. We exploit this symmetry to construct an orthonormal basis for
of bivariate generalised Hermite polynomials of degree n is invariant under rotations. We exploit this symmetry to construct an orthonormal basis for 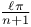 , ℓ=0,...n. Thus we obtain an orthogonal expansion which retains as much of the symmetry of
, ℓ=0,...n. Thus we obtain an orthogonal expansion which retains as much of the symmetry of 