Let p, n ∈ ℕ with 2p ≥ n + 2, and let I a be a polyharmonic spline of order p on the grid ℤ × aℤ n which satisfies the interpolating conditions
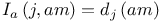
for j ∈ ℤ, m ∈ ℤ n where the functions d j : ℝ n → ℝ and the parameter a > 0 are given. Let
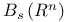
be the set of all integrable functions f : ℝ n → ℂ such that the integral

is finite.
The main result states that for given

there exists a constant c>0 such that whenever
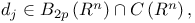
j ∈ ℤ, satisfy

for all j ∈ ℤ there exists a polyspline S : ℝ n+1 → ℂ of order p on strips such that
![$[$] \left| S\left( t,y\right) -I_{a}\left( t,y\right) \right| \leq a^{2p-1}c\cdot D\cdot\left( 1+\left| t\right| ^{\mathbb{\sigma}}\right)$](/math_tex/94b7be4693bad8925b56fd0c1da24eb282.gif)
[$]
for all y ∈ ℝ n , t ∈ ℝ and all 0 < a ≤ 1.
 |
|
О проекте
|
|
О проекте


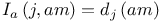 for j ∈ ℤ, m ∈ ℤ n where the functions d j : ℝ n → ℝ and the parameter a > 0 are given. Let
for j ∈ ℤ, m ∈ ℤ n where the functions d j : ℝ n → ℝ and the parameter a > 0 are given. Let 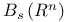 be the set of all integrable functions f : ℝ n → ℂ such that the integral
be the set of all integrable functions f : ℝ n → ℂ such that the integral
 is finite.
is finite.
 there exists a constant c>0 such that whenever
there exists a constant c>0 such that whenever 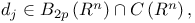 j ∈ ℤ, satisfy
j ∈ ℤ, satisfy  for all j ∈ ℤ there exists a polyspline S : ℝ n+1 → ℂ of order p on strips such that
for all j ∈ ℤ there exists a polyspline S : ℝ n+1 → ℂ of order p on strips such that
![$[$] \left| S\left( t,y\right) -I_{a}\left( t,y\right) \right| \leq a^{2p-1}c\cdot D\cdot\left( 1+\left| t\right| ^{\mathbb{\sigma}}\right)$](/math_tex/94b7be4693bad8925b56fd0c1da24eb282.gif) [$]
[$]
