|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Reinmann H. — The semi-simple zeta function of quaternionic Shimura varieties |
|
|
 |
| Предметный указатель |
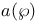 99 99
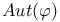 108 108
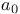 70 70
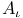 35 35
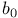 17 17
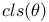 110 110
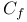 12 12
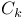 12 12
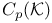 130 130
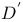 32 32
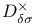 69 71 69 71
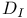 16 16
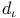 39 39
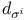 110 110
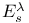 14 14
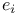 44 44
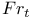 41 49 50 41 49 50
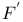 70 70
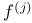 79 79
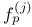 79 79
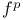 68 68
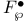 85 85
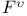 64 64
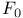 70 70
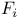 64 64
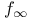 79 79
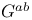 128 128
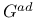 128 128
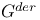 128 128
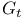 36 36
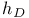 9 9
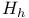 60 60
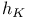 10 10
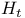 33 33
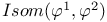 108 108
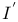 85 85
 39 39
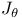 132 132
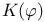 46 46
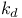 44 44
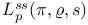 86 86
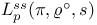 86 86
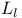 114 114
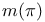 79 79
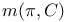 79 79
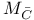 13 13
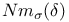 72 72
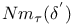 72 72
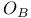 17 17
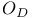 17 70 17 70
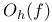 69 69
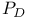 70 70
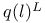 115 115
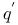 70 70
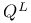 114 114
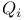 64 64
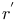 71 71
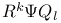 49 49
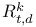 50 50
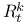 50 50
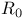 72 72
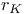 10 10
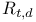 50 50
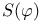 133 133
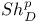 47 47
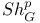 131 131
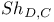 9 9
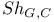 11 11
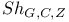 29 29
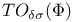 69 69
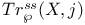 67 67
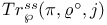 86 86
 22 22
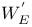 2 2
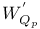 84 84
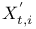 43 43
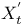 43 43
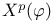 131 131
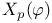 132 132
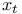 41 41
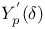 62 62
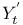 44 44
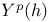 60 60
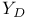 38 38
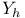 131 131
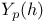 60 60
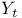 43 43
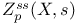 68 68
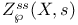 67 67
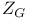 128 128
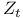 33 33
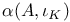 100 100
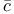 12 12
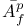 120 120
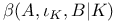 94 94
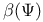 96 96
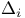 31 31
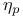 42 42
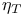 35 35
 106 106
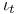 35 35
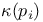 50 50
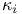 46 46
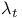 35 35
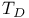 34 34
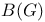 110 110
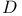 117 117
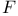 22 22
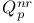 22 22
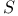 9 9
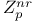 22 22
 78 78
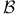 11 11
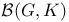 128 128
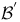 96 96
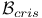 91 91
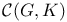 130 130
 109 109
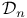 109 109
 132 132
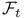 41 41
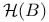 111 124 111 124
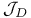 33 33
 30 30
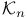 41 41
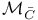 48 48
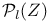 124 124
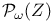 127 127
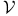 9 9
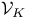 9 17 9 17
 9 70 9 70
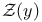 46 46
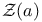 23 23
| 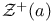 23 23
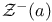 23 23
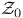 22 22
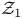 46 46
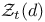 46 46
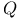 120 120
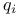 17 17
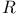 80 80
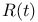 60 60
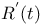 62 62
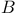 120 120
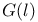 114 114
 106 106
 107 107
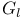 109 109
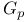 109 109
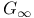 109 109
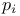 16 16
 127 127
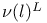 115 115
 117 117
 117 117
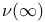 117 117
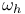 128 128
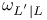 117 117
 65 70 132 65 70 132
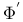 70 70
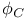 13 13
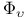 64 70 64 70
 17 17
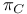 49 49
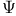 11 17 11 17
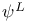 114 114
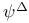 117 117
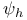 128 128
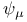 123 123
 22 22
 11 72 11 72
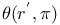 71 71
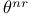 110 110
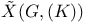 130 130
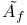 91 91
 29 29
 16 16
 18 18
 41 41
 70 70
 84 84
 31 31
 83 83
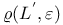 34 34
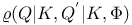 93 93
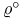 83 83
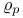 84 84
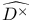 83 83
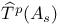 14 14
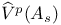 14 14
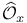 22 30 51 22 30 51
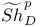 49 49
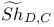 49 49
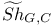 19 19
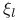 128 128
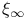 128 128
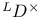 83 83
Abelian scheme 14
Admissible filtration 66 68
Admissible homomorphism 4
Admissible model 59 135
Admissible morphism 54 131 134
Admissible set 29 46 51
Admissible set, minimal 29 46 51
Associated, elements 72 78
Associated, functions 75
Base change lift 76
C-class of isomorphisms 14
Class field theory 10 84
D 9 70
d(Z) 29 46
e 41
E(D) 9
E(K) 10
Element,  -semi-simple 72 -semi-simple 72
Element,  -semi-simple 72 -semi-simple 72
f 9 70
Filtration, admissible 66 68
Filtration, monodromy 85 87
Filtration, Schmid 85
FR 48
G 11
Galois action 10 22 45 51
Galois action, twisted 22 23 27
Groupoid, affine algebraic 108
Groupoid, Dieudonne 109
Groupoid, kernel of 106
Groupoid, neutral 54 107 123 124
Groupoid, pseudo-motivic 120 134
Groupoid, quasi-motivic 120 123
Groupoid, special section of 106 108
inv(x,y) 130
Isogeny type 33 37
K 9 17
L 15 17
l(L) 114
L-function 1 88
L-function, semi-simple 5 67 86 88
L-group 83
Morphisms of groupoids 107
Morphisms of groupoids, equivalent 108 126
Morphisms of groupoids, equivalent algebraically 108
N 39
Orbital integral 69 72 76 78 79
Orbital integral, twisted 69 72 78
p-principal isogeny 14
R 117
Related measures 79
S(t) 49
Scheme 14
Semi-simple trace 67 82 86
Serre condition 123
Sheaf of type (L, 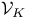 ) 15 ) 15
Shimura variety 1 9—11 131
Shimura variety, admissible model for 59 135
Shimura variety, as moduli scheme 6 14
Shimura variety, dimension of 3 4 88
Shimura variety, Galois twist of 6 13
Shimura variety, reduction of 21 50 106 127
Shimura variety, reduction of, good 30 52 59 88 135
Strict completion 22 48
Unramified conjugacy class 59 135
Vanishing cycles, sheaves of 5 49 51
Vanishing cycles, spectral sequence of 5 68
Weil — Deligne group 2 84
Zeta function 1 3—5 68 88
Zeta function, semi-simple 5 8 67 87 88
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



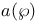
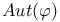
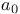
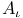
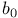
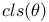
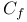
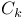
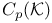
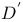
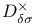
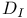
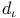
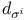
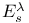
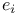
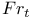
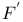
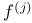
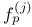
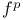
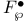
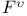
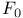
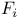
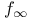
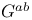
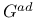
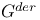
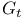
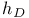
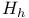
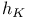
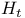
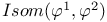
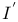

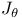
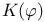
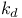
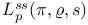
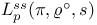
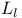
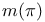
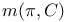
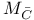
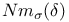
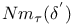
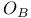
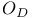
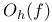
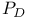
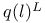
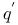
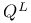
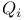
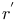
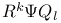
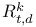
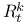
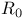
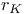
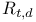
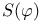
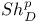
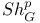
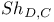
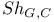
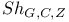
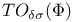
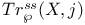
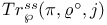
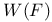
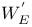
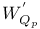
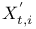
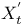
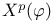
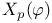
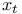
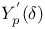
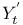
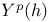
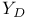
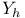
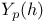
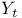
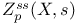
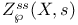
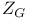
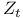
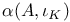
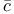
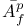
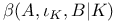
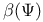
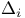
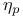
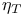

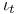
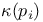
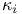
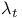
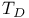
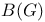
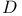
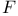
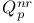
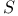
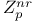

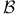
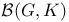
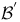
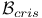
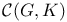

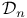

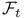
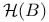
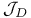

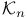
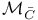
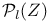
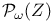
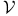
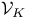

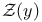
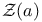
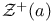
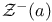
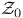
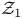
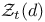
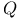
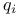
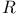
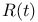
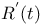
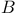
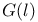
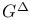
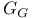
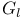
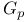
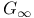
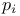
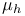
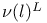
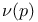
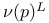
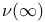
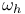
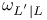

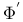
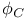
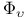

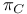
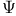
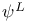
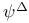
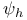
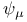


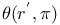
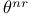
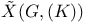
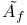
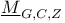
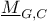
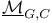
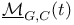
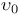
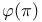
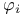
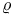
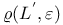
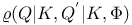
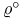
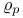
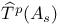
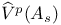
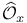
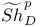
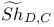
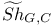
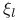
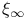
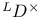
 -semi-simple
-semi-simple