|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Looijenga E.J.N. — Isolated Singular Points on Complete Intersections |
|
|
 |
| Предметный указатель |
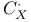 (8.4) (8.4)
 -group (2.C) -group (2.C)
 -monodromy (2.C) -monodromy (2.C)
 -representation (2.C) -representation (2.C)
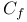 (4.1) (4.1)
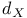 , , 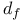 (6.A) (6.A)
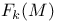 (4.D) (4.D)
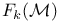 (4.D) (4.D)
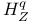 (8.13) (8.13)
 (8.9) (8.9)
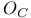 , , 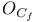 , , 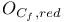 (4.3) (4.3)
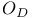 , , 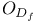 (4.E) (4.E)
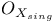 (4.3) (4.3)
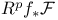 (8.A) (8.A)
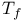 , , 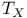 (6.1) (6.1)
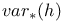 (3.0) (3.0)
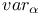 , , 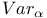 (7.14) (7.14)
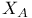 , , 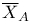 (2.7) (2.7)
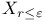 , , 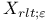 etc. (2.3) etc. (2.3)
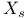 , , 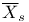 (2.7) (2.7)
 (7.6) (7.6)
 (7.4) (7.4)
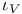 (9.1) (9.1)
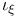 (8.9) (8.9)
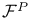 (8.25) (8.25)
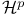 (8.4) (8.4)
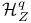 (8.13) (8.13)
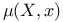 (1.3) (5.11) (1.3) (5.11)
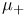 , , 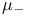 , , 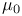 (7.12) (7.12)
 (8.9) (8.9)
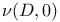 (4. ex. 5) (4. ex. 5)
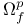 (8.4) (8.4)
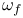 , , 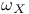 (8.18) (8.18)
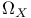 , , 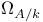 , , 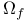 (6.A) (6.A)
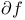 (6.1) (6.1)
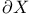 (2.7) (2.7)
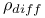 , , 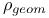 (2.C) (2.C)
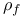 , , 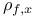 , , 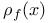 (6.1) (6.1)
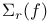 , , 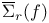 (4.B) (4.B)
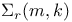 , , 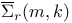 (4.B) (4.B)
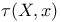 (1.3) (6.1) (1.3) (6.1)
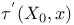 (8.23) (8.23)
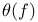 , , 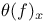 (6.1) (6.15) (6.1) (6.15)
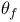 , , 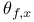 (6.A) (6.15) (6.A) (6.15)
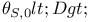 (6.13) (6.13)
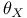 , , 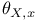 (6.A) (6.A)
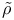 (7.14) (7.14)
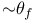 (8.9) (8.9)
 , , 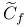 (4.C) (4.C)
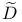 , , 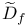 (4.C) (4.C)
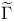 , , 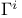 (7.14) (7.14)
(Local) complete intersection algebra (1.9)
Adjacent (singularities) (7.15)
Analytic stratification (2.D)
Base change, commute with base change (4 (4.3)
Bimodal singularity (7.15)
Bouquet of n-spheres (5.10)
C, 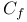 (2.7) (2.7)
Cis(n) (7.15)
Cohomology with supports (8.13)
Complete deformation (6.4)
Complete intersection (1.5)
Complex reflection (1.C)
Cone (2.3)
Connection (8.9)
Contraction with a vector (field) (8.9) (9.1)
Covariant derivative (8.9)
Critical locus (2.7)
Critical space (4.3)
Curvature homomorphism (8.9)
Curve selection lemma (2.1)
Cusp singularity (1.E) (7.23)
D, 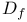 (2.7) (2.7)
De Rham cohomology sheaf (of a map) (8.4)
De Rham complex (of a map) (8.4)
De Rham evaluation map (8.4)
Deformation (6.4) (6.9)
Deformation category (6.4) (6.9)
Derivation (6.A)
Development (4.C) (5.2)
df (6.A)
Differentials, module of (relative, absolute) (6.A)
Discriminant (locus) (2.7)
Discriminant space (4.E)
Distinguished basis (7.5)
Distinguished system of generators (7.5)
Dr (8.4)
Dualizing sheaf (of an icis) (8.18)
E, 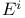 (7.14) (7.14)
Eigenvector (9.B)
| Embedding codimension (1.9)
Embedding dimension (1.9)
Euler derivation (9.9)
Excellent (proper) representative (2.D)
Fitting ideal (4.D)
Fitting ideal sheaf (4.D)
Function which defines a point of an analytic set (2.3)
Function which defines an isolated singularity (2.7)
G, 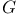 (7.12) (7.12)
Geometric complete intersection (1.5)
Geometric monodromy (2.C)
Geometric monodromy, group (2.C)
Geometric monodromy, representation (2.C)
Good (proper) representative (2.7)
Good C*-action (9.B)
Hessian corank (7.15)
Holomorphic p-form relative a map (8.4)
Horizontal section (8.9)
Hyp(n) (7.15)
Hypersurface germ (1.1)
icis = isolated complete intersection singularity (1.9)
Integrable connection (8.9)
Intersection diagram (7.20)
Isolated hypersurface singularity (1.4)
Kleinian singularity (1. ex. 2 3)
Kodaira — Spencer map (reduced Kodaira — Spencer map) (6.1)
Lie-derivative (8.9)
Liftable vector field (8.9)
Link (2.4)
Local cohomology (8.13)
Local homotopy type (7.3)
m(f) (8.26)
Milnor fibration (2.8)
Milnor fibre (2.8)
Milnor lattice (7.9)
Milnor number (1.4) (5.11)
Miniversal deformation (6.4)
Modality, k-modal (7.15)
mod[(X,x)] (7.15)
Monodromy group (7.B)
Multiplicity (4. ex. 5)
Nilpotent of index 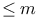 (5.C) (5.C)
Non-quasi-homogeneous companion of triangle singularity (1. ex. 6)
O(V) (8.9)
Period map (9.C)
Picard — Lefschetz formulas (3.1 a)—(3.1 d) (3.3)
Picard — Lefschetz transformation (3.3)
Primitive submodule (7.13)
q.u. = quasi-unipotent (5.C)
q.u. monodromy of index 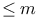 (5.14) (5.14)
Quadratic singularity (1.C) (3.1) (4.2)
Quasi-cone, quasi-conical singularity (1.D)
Quasi-conical variety (1.D)
Quasi-unipotent of index 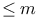 (5.C) (5.C)
Quotient singularity (1.C)
R( ) (8.9) ) (8.9)
Reduced form of a function germ (7.17)
reg (suffix) (2.7)
Regular singularity (of a connection) (8.10)
Represent the local homotopy type (7.3)
Semi-universal deformation (6.4)
Simple part of  (7.9) (7.9)
Simple singularity (7.15)
Simply-elliptic singularity (1. ex. 4) (7.23)
sing (suffix) (2.7) (4.3)
Singular space (4.3)
Smoothing (6.9)
Stein morphism (8.3)
Stratum (2.D)
Tempered growth (of a section) (8.10)
Thom stratification (4.B)
Thom stratum (4.B)
Thom transversal (4.B)
Tjurina number (1.4) (6.1)
Topological connection (8.9)
Triangle singularity (1. ex. 6) (7.23)
Unimodal singularity (7.15)
Unipotent of index 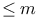 (5.C) (5.C)
Unipotent part of  (7.9) (7.9)
Vanishing cycle (3.4)
Vanishing lattice (7.9)
Variation (homomorphism) (3.1) (7.13)
Variation extension (7.14)
Versal deformation (6.4)
Weight (9.B)
Weighted homogeneous (1.4)
Whitney property (of a stratification) (2.D)
X, 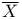 (2.7) (2.7)
Z,Z (7.14)
[(X,x)] (7.15)
[(X,x)] 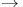 [(Y,y)] (7.15) [(Y,y)] (7.15)
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



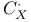
 -group
-group 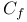
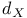 ,
, 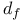
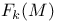
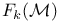
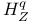

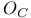 ,
, 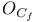 ,
, 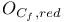
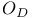 ,
, 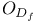
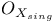
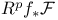
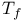 ,
, 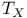
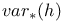
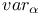 ,
, 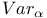
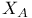 ,
, 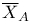
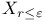 ,
, 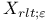 etc.
etc. 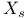 ,
, 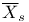


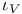
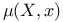
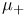 ,
, 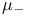 ,
, 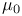

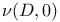
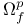
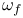 ,
, 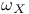
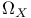 ,
, 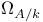 ,
, 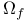
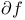
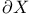
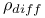 ,
, 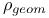
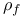 ,
, 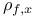 ,
, 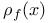
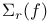 ,
, 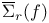
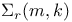 ,
, 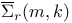
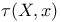
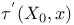
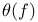 ,
, 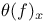
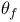 ,
, 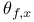
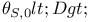
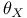 ,
, 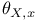
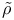
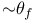
 ,
, 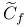
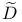 ,
, 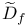
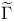 ,
, 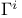
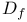
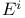
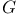
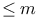
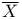
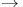 [(Y,y)]
[(Y,y)]