|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kisacanin B. — Mathematical problems and proofs. Combinatorics, Number theory, and Geometry |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
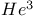 63 63
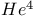 63 63
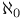 (aleph-zero) 11 13 (aleph-zero) 11 13
 17 195 17 195
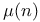 (Mobius mu function) 90 (Mobius mu function) 90
 (golden section) 16 45 51 105 195 (golden section) 16 45 51 105 195
 16 161 191 16 161 191
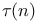 (number of divisors) see “Important functions” (number of divisors) see “Important functions”
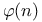 (Euler’s phi function) 42 89 91 95 96 102 (Euler’s phi function) 42 89 91 95 96 102
Abel 160
Abel’s criterion 45
Aborigines 17
Ahmes 191n
AI’Khwarizmi 159
Almagest 157
Anecdote about logician 180
Angletrisection 160 193n
Annals of Mathematics 110
Apollo 160n
Archimedes 121 122 140 191 201
Archimedes’ theorem 131
Archimede’'spiral 160
Arithmetica 109
Arithmeticmean 149 150 174 180 187
Babylon 75
Barr 197
Bernoulli, Daniel 43n 202
Bernoulli, Jakob 43n 167 192
Bernoulli, Johann 43n 202
Bernoulli, Nicolaus (II) 43n 202
Bernoulli, Nicolaus(I) 43n 51
Bhaskara 145
Bijection 10
Binary operation 10
Binet 51
Binet’s formula 51 179 197
Binomial coefficients 28 35—37 52 56—59 64 67 113 170
Binomial formula 26 35—39 45 46 57 60 67 99 178
Boltzmann’s constant 62
Bose — Einstein statistics 62
Bosons 62
Brahma 65
Brahmagupta’s formula 144
Brianchon 138
Brouncker 193
Buffon 193
C 11
Canonical factorization 82 83
Cantor 12
Cardano 160
Cardinality 11
Carmichael numbers 97
Cartesian product 7 14 69
Cauchy 176
Cayley’s Theorem 68
Centroid 130—138
Ceva’s theorem 128 146
Cevian 129
Change for one dinar 49
chebyshev 110
Chebyshev polynomials 179
Chess board 27 34 55 56
Chevalier 160n
Chinese remainder theorem 106
Circle, circumcircle 126—128
Circle, excircle 138
Circle, incircle 126—128 138
Circle, nine-point (Feuerbach’s) 138
Classical constructions 81 160
Classical problems 160 193n
Classical problems, doubling a cube 160 193n
Classical problems, squaring a circle 160 193n
Classical problems, trisecting an angle 160 193n
Codomain 10
Cohen 13
Collinear points 23
Combinations with repetition 33 47
Combinations without repetition 31
Combinations, hybrid 47
Complete residue system 95 96
Conchoid of Nicomedes 160
Concurrent lines 129
Congruences 92
Continuum hypotheses 13
Contradiction 11 16
Converse Ceva’s theorem 129 146
Coplanar points 24
Cotes 194n
Countable set 12
Counterexample 14
Cube duplication 160 193n
De Moivre 45 51 179 196
De Moivre’s Formula 179
Dela Valee-Poussin 110
Delian problem 160n 193n
Derangements 43 56
Descartes 7 109n 161
Dinostratus’ quadratrix 160
Diodes’ cissoid 160
Diophantine equations 101 109 112
Diophantus 109
Dirichlet’s principle 22 53
Disjoint sets 5
Disquisitiones Arithmeticae 92 194
Distribution of primes 110
Divisibility criteria 100 101
dodecahedron 197
Domain 10
Dominos 55 167
Doubling a cube 160n 193n
e 16 41 43 193 194
Egyptian triangle 108
Eight queens 55
Electron 63
Elements 11 38 79 83 85 119 142 167 196
energy levels 61—63
Epimenides 13
Eratosthenes 79
Eubulides 13
Euclid 11 38 79 85 119 167 196
Euclid numbers 179
Euclidean algorithm 83—88 102—106
Euclidean algorithm, complexity of 88
Euclidean algorithm, extended 105
Euclid’s proof of Pythagorean theorem 145
Euclid’s theorem on primes 11 80 167
Euler 43 45 49 51 80 106 140 171 192 195 202
Euler — Venn diagram 4 5 14
Euler's partition theorem 49
Euler’s constant 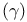 17 195 17 195
Euler’s formula 128 139 156 157 185 194
Euler’s line 136
Euler’s method 112
Euler’s phi function 42 89 91 95 96 102
Euler’s problem partitio numerorum 41
Euler’s theorem in graph theory 54
Euler’s theorem in number theory 42 96 102
Euler’s trinomial 80 177 180
Extended Euclidean algorithm 105
Factorial 28
Factorial, falling factorial 59
Factorial, Stirling’s approximation for 41 61
Factorization of integers 82 83
Fermat 80 109 141 171
Fermat numbers 80 81 160 160n 171
Fermat’s point 140 147 153—155
Fermat’s principle 109n 140
Fermat’s theorem, last 109
Fermat’s theorem, lesser 60 96 99
Fermi — Dirac statistics 63
| fermions 63
Ferrari 160
Feuerbach 197
Feuerbach’s theorem 197
Fibonacci (Leonardo Pisano) 44
Fibonacci’s numbers 44 45 50 51 70 78 87 113 179 197
Fibonacci’s rabbits 44
Finite set 11
Five most important numbers 158 194
Formula for prime numbers 80
Formula, Binet’s 51 179 197
Formula, binomial formula 26 35—39 45 46 57 60 67 99 178
Formula, Brahmagupta’s 144
Formula, de Moivre’s 179
Formula, Euler’s 128 139 156 157 185 194
Formula, Hadamard-de la Valee-Poussin’s 110
Formula, Hamming’s 64
Formula, Hardy —Ramanujan 41 48
Formula, Hero’s 121 126—128 144 151 152
Formula, Leibniz’s 59 192
Formula, Maclaurin’s 45 47 158 180 194
Formula, Mertens’ 195
Formula, Newton’s see “Formula binomial”
Formula, Pascal’s 35 38 47
Formula, polynomial 67
Formula, Stirling’s 41 61
Formula, Sylvester’s 41
Formula, Taylor’s 71 194
Formula, Vandermonde’s 59
Formula, Viette’s 192
Formula, Wallis’ 192
Function see “Multiplicative functions mappings and
Fundamental theorem of algebra 203
Fundamental Theorem of Arithmetic 82
Galois 160 160n
Gauss 81 92 112 160 169 194 202
Gauss’ method 112
Gauss’ Theorem 81
GCD (greatest common divisor) 84
Generating functions 45
Geometric mean 149 150 174 180 187
Gergonne’s point 147
Girard 45
Goat 159
Godel’s theorem 13
Golden section 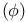 16 45 51 105 195 16 45 51 105 195
Graph theory 54 68
Gregory 192
Gregory’s triangle 170 173 182
hadamard 110
Hamilton — Sylvester’s theorem 138
Hamming’s formula 64
Hanoi towers 65 66
Hardy — Ramanujan’s formula 41 48
Harmonic mean 149 150 174 180 187
Harmonic numbers 19n
Harmonic series 195n
Heegner 83
Heiberg 140n
hermite 16 195
Hero’s formula 121 126—128 144 151 152
Horses 188
Hypotenuse 119
i (imaginary unit) 194
icosahedron 196
Ideal gas 63
Important functions,  (falling factorial) 59 (falling factorial) 59
Important functions, 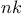 (binomial coefficient) 28 35—37 52 56—59 64 67 113 170 (binomial coefficient) 28 35—37 52 56—59 64 67 113 170
Important functions, 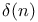 (product of divisors of n) 114 (product of divisors of n) 114
Important functions, 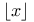 (floor) 43 52 98 (floor) 43 52 98
Important functions, 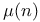 (Mobius f) 90 (Mobius f) 90
Important functions, 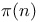 (number of primes < n) 110 (number of primes < n) 110
Important functions,  (sum of divisors of n) 90 (sum of divisors of n) 90
Important functions, 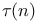 (number of divisors of n) 25 83 89 114 (number of divisors of n) 25 83 89 114
Important functions, 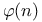 (Euler’s f.) 42 89 91 95 96 102 (Euler’s f.) 42 89 91 95 96 102
Important functions, n! (factorial) 28 41 61
Important points, centroid(T) 130—138
Important points, circumcenter (O) 126 129
Important points, Fermat’s point (F) 140 147 153—155
Important points, Gergonne’s point (G) 147
Important points, incenter(I) 126 127 130
Important points, orthocenter (H) 130 137 138
Induction 37 58 59 167
Inequality of means 149 150 174 180 187
Infinite set 11
Injection 10
Integers 3 75
Integration 140
Internet 75 204
Isomers 69
Jacobi’s theorem 134 139
Jones 191
Knuth 196
Konigsberg bridges 54
Kummer 80
Lagrange 78
Lagrange’s method of multipliers 62
Lambert 193
Lame’s theorem 88
Laplace 45
Law of Cosines 120
Law of Sines 120
lcm (least common multiple) 84
Leibniz 67 97 132 135
Leibniz’s formula 59 192
Leibniz’s theorem 132
Leonardo da Vinci 196
Liber Abaci 44
Lindemann 16 161 193
Linear congruences with one unknown 101
Lucas 45 65
Ludolph van Ceulen 191
Ludolphinenumber 191
Maclaurin series 45 47 158 180 194
Mapping 9
Mapping, bijective 10
Mapping, injective 10
Mapping, surjective 10
Math professor 43
Mathematical induction 37 41 58 59 167
Mathematical tricks and fallacies 142—144 187
Maxwel — Boltzmann’s statistics 42 43
Means 149 150 174 180 187
Mechanical method 140
Mersenne numbers 115
Mertens’ formula 195
Mobius inversion rule 91
Moment of inertia 133 140
Multiplicative functions 89
Multiset 7 29
Napoleon’s triangles 148
Nauck 54
Newton 35—39 194 202
Newton’s binomial formula 26 35—39 45 46 57 60 67 99 178
Numbers, algebraic 16
Numbers, Carmichael 97
Numbers, Euclid 179
Numbers, Fermat 80 81 160 160n
Numbers, Fibonacci 44 45 50 51 70 78 87 113 179 197
Numbers, harmonic 195n
Numbers, Heegner 83n
Numbers, integers 3 75
Numbers, irrational 16
Numbers, Mersenne 115
Numbers, natural 3
Numbers, perfect 115
Numbers, prime 11 25 79
Numbers, pseudoprimes 97 113
Numbers, Pythagorean 75 107 108
Numbers, rational 3 12
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



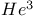
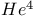
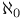 (aleph-zero)
(aleph-zero) 
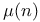 (Mobius mu function)
(Mobius mu function)  (golden section)
(golden section) 
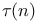 (number of divisors)
(number of divisors) 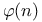 (Euler’s phi function)
(Euler’s phi function) 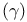
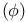
 (falling factorial)
(falling factorial) 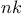 (binomial coefficient)
(binomial coefficient) 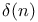 (product of divisors of n)
(product of divisors of n) 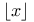 (floor)
(floor) 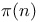 (number of primes < n)
(number of primes < n)  (sum of divisors of n)
(sum of divisors of n)