|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Seress Á. — Permutation Group Algorithms |
|
|
 |
| Предметный указатель |
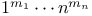 228 228
 7 7
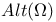 9 9
 11 11
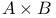 8 8
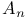 9 9
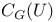 7 7
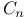 8 8
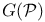 201 201
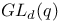 8 8
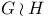 10 10
![$G^{[i]}$](/math_tex/6ea3e9cecfa2a6c2854fd1df5611c0c882.gif) 55 55
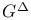 9 9
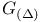 9 9
 10 10
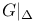 9 9
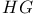 7 7
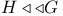 7 7
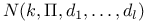 231 231
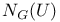 7 7
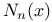 231 231
 207 207
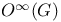 8 8
 11 11
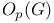 8 8
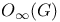 8 8
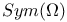 9 9
 9 9
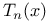 231 231
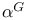 9 9
 9 9
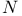 10 10
 10 10
 10 10
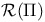 209 209
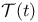 202 202
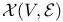 11 11
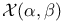 212 212
 94 228 94 228
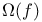 11 11
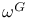 9 9
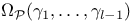 205 205
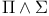 208 208
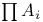 8 8
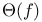 11 11
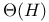 210 210
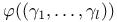 202 202
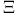 94 228 94 228
() 9
<S> 7
A(m, x) 109
Ackerman function 109 176
Aut(G) 7
Automorphism group 7 129 131 144
Automorphism group of a graph 11 207
Backtrack 53 169 201—217
Base 50 55
Base change 82 97 112 116 134 143 190 204 205
Base, 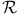 -base 210 -base 210
Base, nonredundant 55
Black-box f-recognizable 192 193 195 196 198
Black-box group 16-47 135 139 192 193 195 228 235—244
Block 9 50 100 107—110 112 113 121 142 190 214
Block homomorphism 81
Block system 9 121 126 128 142 176 178
Block system, maximal 9 191
Block system, minimal 9 132 149 247 253
Block, maximal 9 144 146
Block, minimal 9 101—107 112
Cayley graph 12 26 64
Center 7 50 120 133
centralizer 7 53 117—124 130 134 149 150 152 158 169 172 205 216
Chernoff's bound 31 33—35 37—39
Chernoff's bound, basic-type application 32
Chief series 49 155
Closure 83 111
Closure, G-closure 7 23 38 44 83
Closure, normal closure 7 23 83 111 116 138 140 155 250 251
Collection 17 165
Commutator 8
Complement 7 182
Composition series 50 125—155 158 165 193 197 199
Conjugacy class 172 214—216
Constructive recognition 168 192 193 195 196 227 235—246
Coordinatization 167 169—171 173
Core 8 50 124 180
Core, p-core 8 51 138 157—159
Coset enumeration 184—186
cube 64 67 69
Cube, nondegenerate 65
Cycle type 228
Degree of a graph or hypergraph 11
Degree of a permutation 9
Degree of a permutation group 9
Derived series 8 24 38 49 84 159
Diag(H) 129
Diagonal subgroup 129 131 144 160
Direct product 8 119—122 129 141 147 216
Direct product, projection 8 130
Directed graph 11
Directed graph, out-degree 11
Directed graph, strongly connected 12 112 251
Directed graph, underlying graph 12 219
Double coset 53 203
e(A) 36
Fix(g) 117
| Forest 12 219 249
Frattini argument 170 182
Frobenius group 10 133 137 148 160
G' 8
GF(q) 8
Graph 11
Graph, component 12 112
Graph, connected 12
Hall subgroup 182
Hash function 22 142
Hypergraph 11 87
Hypergraph, uniform 11 87
Inn(G) 7
Labeled branching 218-225
Labeled branching, represents a group 220
Labeled branching, represents a transversal 220
Las Vegas algorithm 14
Local expansion 72
Lower central series 8 24 38 49 84 180
L[i] 12
Markov chain 25 27 215 217
Markov chain, aperiodic 25 28 47 215
Markov chain, irreducible 25 28 215
Markov chain, period of 25 47
Markov chain, stationary distribution of 25 28 215
Markov chain, transition probability 25 28 47 215
Monte Carlo algorithm 13
Nearly linear-time algorithm 51
Nearly uniform distribution 24 29
Nilpotent group 175—182
Nonconstructive recognition 227
normalizer 7 134 137 142 154 170 211
o(f) 11
Orbit 9 18 36 49 60 65 102 112 120—122 141 143 144 154 173 179 189 190 252
Orbit, fundamental 56 83 97 99 182 204 223
Orbital graph 212 251
Ordered partition 207
Ordered partition, cell of 207
Ordered partition, refinement 208
Out(G) 7
Out-degree 11
Path 12 219 252
Perfect group 8 146
Permutation group as black-box group 93 135 138 139 192 193 197
Permutation isomorphism 10 95 119 127 128 140 142 146 173
Polycyclic generating sequence 162 163 165 166 181
Power-conjugate presentation 165—166
Presentation 49 112 165 184 192 194 197—200 227 236 237 244 247 250
Primitive group 9 95 100 126 129—149 160 225 251
Prob(A|B) 30
Product replacement algorithm 27
Random prefix 40
Random subproduct 30—40 73 77 84 88 92 182 245 246 249
Recognition see "Constructive recognition"
Regular graph 11
Regular group 10 78 113 129 133 137 138 146 150 154 160 161
Schreier generator 58 59 62 73 76—78 86 88 92 97 177 198 222 246 249
Schreier tree 56 65 67 70 72 75 77 82 85 88 91 97 99 101 106 118 128 135 136 155 163 190
Schreier tree, shallow 114
Schreier vector see "Schreier tree"
Schreier — Sims algorithm 59
Schur — Zassenhaus theorem 182
Search tree 202
Semiregular group 10 117 123 130
SGS 50 55
SGS, construction 59 63 70 72 75 86 87 90 99 162 193 222 246
SGS, testing 64 77 186 190 193
Siftee 56
Sifting 56
Sifting as a word 86 88 91 128 156 166 167 187
Sifting in a labeled branching 221 223 224
Small-base group 51
Soc(G) 8
Socle 8 51 129 147—149 152—154 161
Solvable radical 8 157—159 216
Solvable residual 8 150 152
Spreader 41
Stabilizer, pointwise 9 49 79 115 127 247
Stabilizer, setwise 10 53 145 176 206
Standard word 93
Straight-line program 10 192—194 197 199 200 227 239 240 243 244 250
Strong generating set see "SGS"
Subdirect product 8 130 160
Subnormal 7 49 124 149 152 160 161 180
supp(g) 9
Support 9
Sylow subgroup 50 95 125 157 161 167—172 182 216
Transitive closure 219 220
Transitive constituent homomorphism 81
Transitive group 9 36 87 117
Transversal 8 56 57 59 65 82 101 118 218 220 246 247 249 253
TREE 12
Tree, breadth-first-search 19 65 68 113 157 187
Tree, rooted 12 108 111 202 219
Tree, rooted, children of a vertex 12
Tree, rooted, leaf 12
Tree, rooted, parent of a vertex 12
union-find data structure 108 113
Up-to-date SGS data structure 59 70 83 88 91
Upper central series 8 179—181
Valency 11
Walk 12 25 212 213 215
Walk, lazy random 26
Wreath product 10 119 122 129 160 226
[A, B] 8
[H, K] 8
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



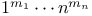

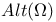

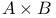
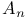
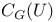
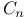
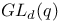
![$G^{[i]}$](/math_tex/6ea3e9cecfa2a6c2854fd1df5611c0c882.gif)
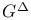
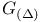

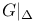
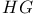
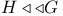
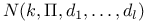
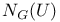
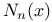

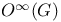

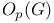
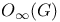
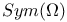

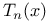
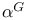

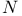


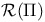
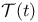
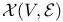
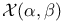

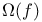
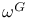
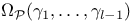
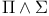
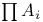
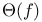
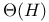
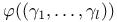
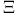
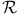 -base
-base