|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Christofides N. — Graph-Theory: an Algorithmic Approach |
|
|
 |
| Предметный указатель |
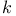 -shortest ( -shortest (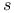 -to- -to-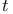 ) paths 167-170 ) paths 167-170
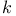 -shortest ( -shortest (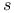 -to- -to-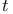 ) paths, algorithm for 169 170 ) paths, algorithm for 169 170
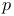 -median 106 108 109 -median 106 108 109
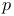 -median, absolute 110 -median, absolute 110
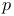 -median, approximate algorithm for 116-118 -median, approximate algorithm for 116-118
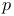 -median, generalised 110 111 116 -median, generalised 110 111 116
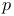 -median, integer programming method for 112 113 -median, integer programming method for 112 113
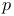 -median, tree search algorithms for 113-116 -median, tree search algorithms for 113-116
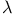 -optimality 117 118 -optimality 117 118
(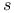 -to- -to-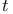 ) shortest path problem 150-163 ) shortest path problem 150-163
(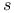 -to- -to-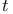 ) shortest path problem, in directed acyclic graphs 170-174 ) shortest path problem, in directed acyclic graphs 170-174
(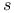 -to- -to-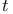 ) shortest path problem, with general costs 157-163 ) shortest path problem, with general costs 157-163
(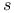 -to- -to-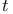 ) shortest path problem, with general costs, algorithm for 158 ) shortest path problem, with general costs, algorithm for 158
(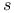 -to- -to-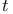 ) shortest path problem, with non-negative costs 152-157 ) shortest path problem, with non-negative costs 152-157
(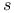 -to- -to-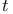 ) shortest path problem, with non-negative costs, Dijkstra's algorithm for 152-157 ) shortest path problem, with non-negative costs, Dijkstra's algorithm for 152-157
4-colour conjecture 62
5-colour theorem 62
Adjacency matrix 13
Adjacency matrix, modified variable 217
Adjacent arcs 4
Adjacent vertices 4
Arborescence see Directed tree
ARC 1
Arc, backward 285 326
Arc, capacity of 175 282
Arc, cost of 5
Arc, forward 285 326
Arc, gain of 325
Arc, length of 5
Arc, lower bound on flow in 282 299
Arc, reliability of 174
Arc, weight of 5
Assembly line balancing 48
Assignment problem 342 373-379
Assignment problem, an algorithm for 374
Assignment problem, an algorithm for (matrix form) 374 375
Base 254
Basis 24-27
Basis, contra 25
Basis, power 26
Betti number see Cyclomatic number
Blossom 346-350
Blossom, outermost 346
Blossom, shrinking of 346-350
Boolean expression (logical expression) 48
Centre 79-105
Centre, absolute 83-92
Centre, absolute in 84
Centre, absolute out 84
Centre, Hakimi's algorithm for absolute 85 86
Centre, in 82
Centre, in-out 83
Centre, modified Hakimi's algorithm for centre, absolute 90 91
Centre, out 82
Chain 4
Chain, elementary 5
Chain, simple 5
Chinese postman problem 203-208
Chinese postman problem, algorithm for 204 205
Chromatic number 58
Chromatic number, lower bounds on 60 61
Chromatic number, upper bounds on 61 62
Circuit 6
Circuit, elementary 6
Circuit, Eulerian 199-212
Circuit, Eulerian, Fleury's rule for construction of 202
Circuit, fundamental 191-193
Circuit, fundamental, matrix of 198 211
Circuit, Hamiltonian 6 135 210 214-281
Circuit, Hamiltonian, algebraic method for the generation of 217-221
Circuit, Hamiltonian, algorithm of Roberts & Flores for the generation of 221-225
Circuit, Hamiltonian, comparison of methods for the generation of 230-233
Circuit, Hamiltonian, multipath method for the generation of 225-230
Circuit, independent 190
Circuit, optimal, in doubly-weighted graphs 166 167
CLIQUE 30 32 33
Clique number 30 33 60
Closeness of tree to a path 240
Cocyclomatic number 190
Colouring 58-78
Colouring problem 58
Colouring problem, a direct tree search algorithm for 70 71
Colouring problem, a dynamic programming method for 62-66
Colouring problem, a set covering algorithm for 68-70
Colouring problem, a zero-one programming method for 66-68
Colouring problem, approximate algorithms for 71 72
Colouring, optimal independent 63 66
Component 12
Component, strong 12 21-24
Component, unilateral 12
Component, weak 12
Compression of a matrix 269
Contraction of solution to assignment problem 267-269
Correspondence 1
Correspondence, inverse 3
Covering 49 50 340
Covering, minimum 49 50 340
Covering, problem of minimum (CP) 340 383 384
Covering, problem of minimum cardinality (CCP) 341 383 384
CPM 170
Crew scheduling 48
Critical path 171-174
Cut-set 175-179 193-197 284 285
Cut-set, directed 195 196
Cut-set, fundamental 196 197
Cut-set, fundamental, matrix 198 211
Cut-set, proper 194 195
Cut-set, value of 284
CYCLE 6
Cycle, active 328-334
Cyclomatic number 190
Degree 7
Degree, k-step 72
Degree-constrained partial graph problem 339 379-383
Delivery of post 203
density see Clique number
Diameter 92 104
Dominance number 30
Dominating (vertex) set 27 35-38
Dominating (vertex) set, minimal 35
Dominating (vertex) set, minimum 35
Dominating link set see Covering
Dominating link set, minimum see Minimum covering
Electrical wiring 66
Externally stable set see Dominating set
Flow 282
Flow problem 282
Flow problem, (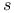 -to- -to-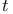 ) maximum 282-296 ) maximum 282-296
Flow problem, (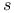 -to- -to-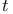 ) maximum, labelling algorithm for 286 287 ) maximum, labelling algorithm for 286 287
Flow problem, (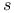 -to- -to-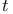 ) minimum cost 282 308-324 ) minimum cost 282 308-324
Flow problem, (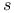 -to- -to-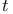 ) minimum cost, dual algorithm for 323-324 ) minimum cost, dual algorithm for 323-324
Flow problem, (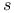 -to- -to-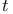 ) minimum cost, primal algorithm for 309-312 ) minimum cost, primal algorithm for 309-312
Flow problem, between every pair of vertices 282-300
Flow problem, between every pair of vertices, algorithm for 302-304
Flow problem, in graphs with arc gains 283 325-334
Flow problem, in graphs with arc gains, algorithm for 330 331
Flow problem, multicommodity 283 297
Flow, conformal 295
Flow, decomposition of 293-296
Flow, in graphs with arc and vertex capacities 297 298
Flow, in graphs with convex arc costs 322 323
Flow, in graphs with gains at vertices 335
Flow, in graphs with many sources and sinks 296 297
Flow, in graphs with upper and lower bounds on arc flows 299 300
Flow, maximum, in graphs with gain 326
Flow, optimum maximum, in graphs with gain 326
Flow, optimum, in graphs with gain 326
Flow, value of 284
Flow-augmenting chain 285
Flow-augmenting chain in graphs with gain 326-328
| Flow-augmenting chain in graphs with gain, capacity of 328
Flow-augmenting chain in graphs with gain, gain of 327
Flow-equivalence 301
Graph, antisymmetric 9
Graph, arc-weighted 5
Graph, bipartite 10 373 380
Graph, complementary 32
Graph, complete 8
Graph, complete antisymmetric 9
Graph, complete symmetric 9
Graph, definition 1
Graph, directed 1
Graph, disconnected 12
Graph, equality partial 361
Graph, incremental 293 310 312 322 324 331
Graph, Kuratowski 11
Graph, line 210
Graph, Moon - Moser 53
Graph, nondirected 1
Graph, nondirected counterpart to 1
Graph, nonplanar 12
Graph, partial 7
Graph, planar 11 62
Graph, r-chromatic 58
Graph, reduced 225
Graph, strong, (strongly connected) 12
Graph, symmetric 9
Graph, transitive 21
Graph, unilateral 12
Graph, unitary 295
Graph, vertex-weighted 5
Graph, weak 12
Hungarian algorithm 373
Hungarian algorithm, for assignment problem 373-375
Hungarian algorithm, for transportation problem 381
Incidence matrix 14 126 132 145 198 211 349
Indegree 7
Independence number 30 31
Independent (vertex) set 31
Independent (vertex) set, maximal 31-34 60 63 68 69
Independent (vertex) set, maximum 31
Independent link set see Matching
Independent link set, maximum see Maximum matching
Information transmission 53
Information, retrieval 47
Inspection of electric or railway lines 203
Internal vertex product 217
Internally stable set see Independent set
Iterative method for absolute 91 92
K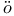 nig and Hall theorem 384 nig and Hall theorem 384
K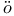 nig's theorem 386 nig's theorem 386
K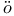 nigsberg bridge problem 199 nigsberg bridge problem 199
Labyrinth, traversal of 212
Link, artificial 204 205
Link, definition 1
Link, shorting of 176-178
Loading problem 73 74
Location 79
Location, minimax, problem 79 106
Location, minisum, problem 79 106
Location, of a depot 108
Location, of an emergency centre 82 83 86-90
Location, of centres 36 37 79-105
Location, of many emergency centres 93 94
Logical expression, simplification of 48
Loop 5
Mapping 1
Matching 49 50 339-388
Matching, maximum 49 50 340
Matching, maximum cardinality 341
Matching, maximum cardinality, algorithm for 352 353
Matching, maximum, algorithm for 361-366
Matching, perfect 359
Maximum-flow minimum-cut theorem 284 285
Median 79 106-121
Median, absolute 109 110
Median, in 107
Median, out 107
Median, p-in 109
Median, p-out 109
Negative cost circuit 158 164-167 312 314 324
Network attack or defence 48
Network attack or defence, network flows 282-338
Network planning 48
Null set 1
Nullity see Cyclomatic number
Organisational structure 26
Out-of-kilter algorithm 309 321
Outdegree 7
P-centre 27 92 93
P-centre, absolute 94 95
P-centre, algorithm for 101-103
P-centre, algorithm for absolute 95-103
Path, alternating 342
Path, augmenting, (relative to a flow) see Flow-augmenting chain
Path, augmenting, (relative to a matching) 343
Path, capacity of 175
Path, cardinality of 5
Path, definition 3
Path, deviation from 168 169
Path, elementary 4
Path, Eulerian 199 201 202
Path, Hamiltonian 214-281
Path, largest expected capacity 179-183
Path, largest expected capacity, algorithm for 180 181
Path, length of 5
Path, longest 171-174
Path, most reliable 174 175
Path, reliability of 174
Path, simple 4
penetration 95
PERT 170
Political districting 48
Predecessol label 129
Predecessol label, change in 130
Project selection 32
Queens on chessboard 53
r-subgraph 62
r-subgraph, maximal 62-66
RADIUS 82
Radius, absolute in 84
Radius, absolute out 84
Radius, in 82
Radius, in-out 83
Radius, out 82
Reachability matrix 17
Reachability matrix, limited 21
Reachable 17
Reachable, set 18
Reaching matrix 18
Reaching matrix, limited 21
Reaching set 19
Reduced matrix 374
Refuse collection 203
Region 95
Resource, allocation 75
Resource, levelling 173
Root of alternating tree 345
Root of directed tree 123
Root of directed tree, change in 130
s-graph 181 201
Scheduling a processing facility 214 233-235
See also Hamiltonian circuit) path, largest capacity 175-179
Separation 80-82
Separation, in 81
Separation, out 81
Set covering problem, (SCP) 31 39-47 100
Set covering problem, (SCP), applications of 47-51
Set covering problem, (SCP), dominance tests for 43-44
Set covering problem, (SCP), lower bound for 44-46
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



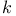 -shortest (
-shortest (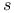 -to-
-to-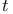 ) paths
) paths 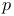 -median
-median 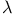 -optimality
-optimality  nig and Hall theorem
nig and Hall theorem