|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Marcja A., Toffalori C. — A Guide to Classical and Modern Model Theory |
|
|
 |
| Предметный указатель |
Recursive sets 39
Recursively enumerable set 40
Residue field 99
Ressayre’s Uniqueness theorem 202 271
Ring, commutative 107
Ring, differential 109
Ring, existentially closed 106
Ring, ordered 317
Ring, reduced 109
Rings, elementary class of 105
Robinson’s Test 88—91
Rudin — Keisler relation 254 290
Ryll — Nardzewski’s theorem 217 220
SchanuePs Conjecture 343
Semialgebraic set 38 67 134
Semidefinite positive 95
Sentence 5 7
Separant 211
Shelah’s uniqueness theorem 220 270— 273 290
Sign change property 98
Small subset of Q 148
Smooth equivalence relation 223
Spectrum function 226
Stationarity over models 236
Stationary logic 290
Strong homogeneity theorem 147
Strongly minimal set 163 168—172 288 304
Structure,  345 345
Structure,  5 344 5 344
Structure,  341 341
Structure,  -stable 185 220 291 308 -stable 185 220 291 308
Structure, basis of 177
Structure, definable 40 121 302
Structure, dimension of 177
Structure, existentially closed 105 110 119
Structure, expansion of 5
Structure, extension of 85
Structure, interpret able 123
Structure, locally modular 283
Structure, minimal 77 168 176 179
Structure, o-minimal 78 178 179 313 318
Structure, restriction of 5
Structure, simple 232
Structure, stable 236
Structure, strongly minimal 168 256 282 287 292 308
Structure, superstable 241
Structure, trivial 283
Structure, two-sorted 100
Structure, universe of 2
Structure, unstable 236
Structure, X-definable 121
Structure, X-interpretable 123
structures 2
Structures, elementarily equivalent 10
Subanalytic set 344
Subanalytic set, globally 344
Subexponential set 342
Subgroup, definable, connected 188
Subgroup, pp-definable 41 69
Submodule, pure 151
Substructure 5 85
Substructure, elementary 14
Substructure, existential 15
Substructure, finitely generated 5
Substructure, generated 5
Successor 47 263
Symmetry 228 234
Tarski — Seidenberg theorem 38 67
Tarski — Vaught theorem 17 158
Tarski’s theorem 54 296 341
Terjanian’s counterexample 100 102
Terms 6
Theory 21 22
Theory of a class of models 21
Theory of a model 31
Theory of an equivalence relation 256
Theory of infinite sets 32 282
Theory of two equivalence relations 265
Theory of vectorspaces 34
Theory,  33 57 87 33 57 87
Theory,  26 32 33 45 57 77 88 149 169 184 197 219 261 26 32 33 45 57 77 88 149 169 184 197 219 261
Theory,  111 112 197 209—217 287 111 112 197 209—217 287
Theory,  115 115
Theory,  48 50 51 77 87 48 50 51 77 87
Theory,  24 32 52 53 160 174 181 182 217 218 226 24 32 52 53 160 174 181 182 217 218 226
Theory,  114 114
| Theory, 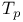 102 102
Theory,  27 27
Theory,  -categorical 28 -categorical 28
Theory,  -stable 181—184 220 230 242 261 270 346 -stable 181—184 220 230 242 261 270 346
Theory,  68 70 73 68 70 73
Theory, ACF 26 45 54 58 88 91 111
Theory, ACF A 117 118 131 231 288
Theory, Booleanly A-categorical 219
Theory, categorical 133 274
Theory, classifiable 225 227 261—270
Theory, complete 19 30 102
Theory, completions of 31 45
Theory, consistent 21
Theory, decidable 40 44 342
Theory, deep 268
Theory, depth of 268
Theory, dLO 52
Theory, independence system of 228
Theory, kT 169
Theory, model companion of 105 117
Theory, model complete 34 46 85—96 102 103 117 119 212 288 342 344 345
Theory, not classifiable 237
Theory, o-minimal 78—79 178 226 234 313 344 345 348
Theory, presentable 264
Theory, RCF 27 33 61 65 66 80 87 88 91 93 95 104 111 129 175 197 341
Theory, rich 19
Theory, rosy 348
Theory, shallow 268
Theory, simple 227—235 249 289 290 328
Theory, stable 235—239 243
Theory, strongly minimal 76—77 163 168 182 184 220 221 225 227 236 239 261 274 346
Theory, superstable 239—242 252
Theory, totally transcendental 133 181 184 346
Theory, unstable 236 237
Theory, weakly o-minimal 346
Thorn-independence 348
Topological space, compact 140
Topological space, hausdorff 140
Topological space, totally disconnected 140
Transcendence basis 170 295
Transcendence degree 33 92 149 170 294
Transitivity 228 234
TREE 264
Tree, rank of 267
Tree, well founded 267
Trichotomy theorem 341
Turing machine 39 79 80
TYPE 133 136—143
type of 138
Type, algebraic 141 166
Type, complete 137
Type, consistent 137
Type, definable 238 244
Type, depth of 268
Type, generic 190 294
Type, isolated 141 156 198
Type, realization of 139
Type, regular 241
Type, RK-minimal 255
Type, stabilizer of 188
Type, stationary 240
Type, strongly regular 256
Ultrafilter 136
Uniqueness theorem 146
Universal domain 86
Universality Theorem 145
Valuation map 99 101
Valuation ring 99
Variety, abelian 304
Variety, algebraic 37 285 292 299
Variety, irreducible 293 294 298
Vaught’s conjecture 290 329
Vaught’s theorem 32
Vectorspace 230 239
Vectorspace, structure of 4
Vectorspace, theory of quantifier elimination for 75
Weak homogeneity theorem 145
Well ordered sets, class of 24
Word problem 107
Zariski geometries 285
Zariski structure 286
Zariski topology 38 117 292 296 297 302
Ziegler spectrum 154
Zilber’s conjecture 279—286 289 309 340
Zilber’s Indecomposability theorem 190 309
Zorn’s Lemma 94
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте






 -stable
-stable 






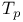

 -categorical
-categorical 