|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Владимиров Д.А. — Булевы алгебры |
|
|
 |
| Предметный указатель |
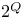 -алгебра всех подмножеств множества -алгебра всех подмножеств множества 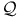 25 25
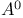 -нормальное ядро множества А 114 -нормальное ядро множества А 114
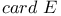 -мощность множества Е 301 -мощность множества Е 301
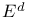 -дизъюнктное дополнение множества Е 45 46 -дизъюнктное дополнение множества Е 45 46
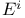 -совокупность нижних границ множества Е 11 -совокупность нижних границ множества Е 11
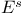 -совокупность верхних границ множества Е 11 -совокупность верхних границ множества Е 11
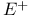 -совокупность ненулевых элементов множества Е 17 -совокупность ненулевых элементов множества Е 17
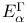 , , 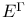 -метрическая структура, ассоциированная с произвольным произведением лебеговских мер 85 -метрическая структура, ассоциированная с произвольным произведением лебеговских мер 85
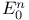 -метрическая структура измеримых по Лебегу множеств -метрическая структура измеримых по Лебегу множеств 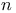 -мерного единичного куба 85 -мерного единичного куба 85
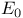 -метрическая структура (алгебра mod 0) измеримых по Лебегу множеств отрезка [0,1] 85 -метрическая структура (алгебра mod 0) измеримых по Лебегу множеств отрезка [0,1] 85
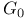 -алгебра регулярных открытых множествна (0,1) 55 -алгебра регулярных открытых множествна (0,1) 55
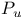 -оператор проектирования 49 50 -оператор проектирования 49 50
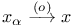 , , 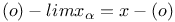 -предел 124 -предел 124
![$[E]_{\mathfrak{u}}$](/math_tex/cb6ea7b4a8963d40cef23e8235fd911782.gif) -след множества Е 50 -след множества Е 50
 -пространство 180 -пространство 180
 -пространство расширенное 188 -пространство расширенное 188
 -подалгебра, порожденная множеством Е 67 -подалгебра, порожденная множеством Е 67
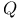 , , ![${\mathfrak{Q}}[\mathcal{X}]$](/math_tex/26357671189f82c1ea373ce2a686cd4b82.gif) -реализующий (стоуновский) компакт булевой алгебры -реализующий (стоуновский) компакт булевой алгебры 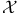 40 40
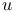 -подалгебра 66 -подалгебра 66
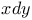 -дизъюнктность элементов х, у 18 -дизъюнктность элементов х, у 18
 -независимость 103 -независимость 103
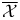 -булева алгебра компонент алгебры -булева алгебра компонент алгебры 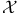 51 51
 -правильная подалгебра, порожденная множеством Е 108 -правильная подалгебра, порожденная множеством Е 108
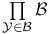 -произведение подалгебр класса -произведение подалгебр класса 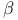 240 241 240 241
 -алгебра множеств 107 -алгебра множеств 107
 -идеал 107 -идеал 107
 -полнота б.а. 106 107 -полнота б.а. 106 107
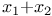 -сумма элементов булевой алгебры 22 -сумма элементов булевой алгебры 22
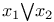 -верхняя грань элементов -верхняя грань элементов 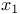 , , 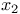 11 11
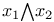 -нижняя грань элементов -нижняя грань элементов 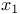 , , 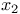 11 11
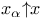 , , 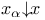 -монотонная сходимость 126 -монотонная сходимость 126
 -алгебра, порожденная системой всех промежутков, содержащихся в <а,Ь> 92 -алгебра, порожденная системой всех промежутков, содержащихся в <а,Ь> 92
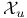 -главный идеал булевой алгебры -главный идеал булевой алгебры 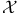 36 37 36 37
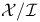 , , 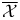 -фактор-алгебра 77 80 -фактор-алгебра 77 80
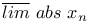 -общее значение верхних пределов всевозможных подпоследовательностей последовательности { -общее значение верхних пределов всевозможных подпоследовательностей последовательности {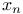 } 138 } 138
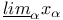 , , 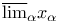 -нижний и верхний пределы 125 -нижний и верхний пределы 125
(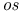 )-топология 124 135 )-топология 124 135
(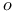 )-сходимость 124 )-сходимость 124
(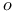 )-топология 124 135 )-топология 124 135
0-нуль частично упорядоченного множества 17
1-единица частично упорядоченного множества 17
f-разложение единицы 190
Автоморфизм 61 115 280
Автоморфизм эргодический 62
Алгебра множеств 30—33 35 39 43
Атом 116
Булева алгебра (б.а.) 19
Булева алгебра (б.а.)  -разложимая 263 -разложимая 263
Булева алгебра (б.а.)  -полная 106 -полная 106
Булева алгебра (б.а.) вполне однородная 291
Булева алгебра (б.а.) вырожденная 19
Булева алгебра (б.а.) дискретная (атомическая) 116
Булева алгебра (б.а.) компонент 51
Булева алгебра (б.а.) лебеговская 85
Булева алгебра (б.а.) непрерывная 117
Булева алгебра (б.а.) нормированная 58 202—208
Булева алгебра (б.а.) однородная 262
Булева алгебра (б.а.) полная 106
Булева алгебра (б.а.) разложимая 263
Булева алгебра (б.а.) регулярная 223
Булева алгебра (б.а.) регулярных открытых множеств 53—55 105 146 147 152 224
Булева алгебра (б.а.) свободная 99
Булева алгебра (б.а.) сепарабельная 211 258 269 274
Булева алгебра (б.а.) счетного типа 56 57
Булево кольцо 75
Гомоморфизм 80
Гомоморфизм  -непрерывный 160 -непрерывный 160
Гомоморфизм естественный 81
Гомоморфизм непрерывный 160
Границы множеств 11
Границы точные (грани) 11
Дизъюнктное разложение 50
Дизъюнктность элементов 18
Дистрибутивность 16 17
Дистрибутивность б.а. 23 24
Дистрибутивность слабая счетная 230 234
Дополнение дизъюнктное множества 46
Дополнение элемента 18
Идеал 35 46 47
Идеал главный 37 46—49
Идеал дуальный 10
Идеал максимальный 37
Идеал собственный 36
Идеал, порожденный данным множеством 36
Изоморфизм 10 81
Изотонность 10 13 81
Квазимера 55
Квазимера существенно положительная 56
Компонента 47
Компонента  -пространства 180 181 -пространства 180 181
Компонента 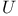 -инвариантная 62 -инвариантная 62
Компонента 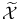 -однородная 257 -однородная 257
| Компоненты положительности и отрицательности вполне аддитивной функции 158
Лемма Куратовского — Цорна 303
Математическое ожидание 201
Мера 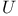 -инвариантная 63 280 -инвариантная 63 280
Мера булева 92 193
Мера вероятностная 58
Мера инвариантная 63 115 116 291
Мера основная 58 63
Мера спектральная 193 234
Мера условная 221
Метрика в б.а. 64 203
Метрическая структура, ассоциированная с измеримым пространством 86 199 207 208 211 220 228 274
Множество d-правильное 113
Множество линейно упорядоченное 303
Множество минорантное 111
Множество направленное 119
Множество открыто-замкнутое 39
Множество открытое регулярное 53
Множество полное в б.а. 46
Множество частично упорядоченное 303
Мономорфизм 81
Направление 119
Независимость 95
Независимость метрическая 103
Подалгебра 65
Подалгебра  -простейшая 256 -простейшая 256
Подалгебра  -правильная 108 -правильная 108
Подалгебра борелевская 109
Подалгебра вырожденная 65
Подалгебра правильная 108
Подалгебра простейшая 65 67
Подалгебра, насыщающая компоненту 243
Подалгебра, порожденная данным множеством 67
Полином 70
Полином элементарный 70
Полнота б.а. 106 107
Последовательность 119
Последовательность обобщенная 119
Последовательность простая 301
Принцип двойственности 14
Принцип диагонали 207
Принцип исчерпывания 112
Продолжение гомоморфизмов 169—178
Разбиение элемента б.а. 67
Разложение единицы 190
Разность элементов б.а. 22
Сегмент 133 303
Сепарабельность б.а. 211
Симметрическая разность 21
Система образующих 67
След множества 50
След подалгебры в компоненте 242
Случайная величина 201
Соединение булевых алгебр 51
Спектральное семейство 189
Спектральные функции 189
Спектральные функции почти совпадающие 189
Структура 16
Структура векторная ( -линеал) 179 -линеал) 179
Сумма элементов б.а. 22
Сх-дополнение элемента в булевой алгебре 19
Теорема Гливенко — Стоуна 151
Теорема Лебега — Каратеодори 166 167
Теорема о нормальных ядрах 114
Теорема Пинскера 225 226
Теорема Сикорского 87—90
Теорема Стоуна 40—44
Теорема Стоуна — Огасавара 110
Теорема Хайана — Какутани 299 300
Топологии порядка 124
Топологическая сходимость 124
Топология 304
Топология монотонная 142
Топология равномерная 141
у-х - разность элементов булевой алгебры 22
Фактор-алгебра 80
Фильтр 39
Функция аддитивная 55 157
Функция вполне аддитивная 57 157
Функция распределения 201 212
Функция счетно-аддитивная 58 157
Частичное упорядочение 302
Число Келли 227
Элементы 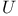 -конгруэнтные 63 280 -конгруэнтные 63 280
Элементы делимые 292
Элементы конгруэнтные 280
Элементы положительности и отрицательности вполне аддитивной функции 158
Элементы равносоставленные 280
Эпиморфизм 81
Ядро гомоморфизма 81
Ядро нормальное 114
{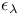 }-спектральное семейство 189 }-спектральное семейство 189
|x-y|, 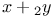 -симметрическая разность элементов булевой алгебры 21 -симметрическая разность элементов булевой алгебры 21
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



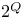 -алгебра всех подмножеств множества
-алгебра всех подмножеств множества 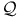
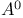 -нормальное ядро множества А
-нормальное ядро множества А 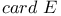 -мощность множества Е
-мощность множества Е 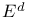 -дизъюнктное дополнение множества Е
-дизъюнктное дополнение множества Е 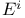 -совокупность нижних границ множества Е
-совокупность нижних границ множества Е 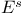 -совокупность верхних границ множества Е
-совокупность верхних границ множества Е 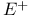 -совокупность ненулевых элементов множества Е
-совокупность ненулевых элементов множества Е 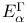 ,
, 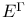 -метрическая структура, ассоциированная с произвольным произведением лебеговских мер
-метрическая структура, ассоциированная с произвольным произведением лебеговских мер 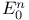 -метрическая структура измеримых по Лебегу множеств
-метрическая структура измеримых по Лебегу множеств 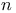 -мерного единичного куба
-мерного единичного куба 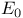 -метрическая структура (алгебра mod 0) измеримых по Лебегу множеств отрезка [0,1]
-метрическая структура (алгебра mod 0) измеримых по Лебегу множеств отрезка [0,1] 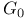 -алгебра регулярных открытых множествна (0,1)
-алгебра регулярных открытых множествна (0,1) 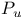 -оператор проектирования
-оператор проектирования 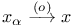 ,
, 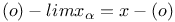 -предел
-предел ![$[E]_{\mathfrak{u}}$](/math_tex/cb6ea7b4a8963d40cef23e8235fd911782.gif) -след множества Е
-след множества Е  -пространство
-пространство  -подалгебра, порожденная множеством Е
-подалгебра, порожденная множеством Е 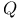 ,
, ![${\mathfrak{Q}}[\mathcal{X}]$](/math_tex/26357671189f82c1ea373ce2a686cd4b82.gif) -реализующий (стоуновский) компакт булевой алгебры
-реализующий (стоуновский) компакт булевой алгебры 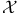
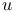 -подалгебра
-подалгебра 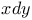 -дизъюнктность элементов х, у
-дизъюнктность элементов х, у  -независимость
-независимость 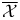 -булева алгебра компонент алгебры
-булева алгебра компонент алгебры  -правильная подалгебра, порожденная множеством Е
-правильная подалгебра, порожденная множеством Е 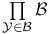 -произведение подалгебр класса
-произведение подалгебр класса 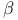
 -алгебра множеств
-алгебра множеств 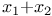 -сумма элементов булевой алгебры
-сумма элементов булевой алгебры 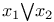 -верхняя грань элементов
-верхняя грань элементов 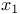 ,
, 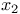
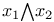 -нижняя грань элементов
-нижняя грань элементов 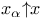 ,
, 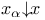 -монотонная сходимость
-монотонная сходимость  -алгебра, порожденная системой всех промежутков, содержащихся в <а,Ь>
-алгебра, порожденная системой всех промежутков, содержащихся в <а,Ь> 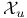 -главный идеал булевой алгебры
-главный идеал булевой алгебры 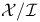 ,
, 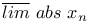 -общее значение верхних пределов всевозможных подпоследовательностей последовательности {
-общее значение верхних пределов всевозможных подпоследовательностей последовательности {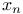 }
} 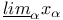 ,
, 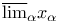 -нижний и верхний пределы
-нижний и верхний пределы 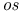 )-топология
)-топология 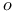 )-сходимость
)-сходимость 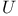 -инвариантная
-инвариантная 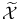 -однородная
-однородная 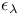 }-спектральное семейство
}-спектральное семейство 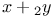 -симметрическая разность элементов булевой алгебры
-симметрическая разность элементов булевой алгебры