|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lewis J.D. — CRM Monograph Series, vol.10: A Survey of the Hodge Conjecture |
|
|
 |
| Предметный указатель |
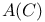 (underlying complex torus of Abelian variety A) 299 (underlying complex torus of Abelian variety A) 299
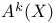 272 272
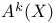 (Chow group of cycles algebraically equivalent to zero) 173 (Chow group of cycles algebraically equivalent to zero) 173
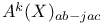 (Chow group of cycles Abel — Jacobi equivalent to zero) 265 (Chow group of cycles Abel — Jacobi equivalent to zero) 265
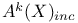 (Chow group of cycles incident equivalent to zero) 265 (Chow group of cycles incident equivalent to zero) 265
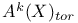 (torsion subgroup) 186 (torsion subgroup) 186
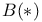 (standard Lefschetz conjecture) 258 (standard Lefschetz conjecture) 258
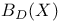 (blow-up of X along a manifold D) 21 (blow-up of X along a manifold D) 21
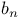 (X) (Betti number) 193 (X) (Betti number) 193
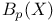 (blow-up of X at a point p) 21 (blow-up of X at a point p) 21
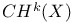 (Chow group) 173 (Chow group) 173
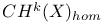 (Chow group of cycles homologous to zero) 173 (Chow group of cycles homologous to zero) 173
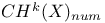 (Chow group of cycles numerically equivalent to zero) 273 (Chow group of cycles numerically equivalent to zero) 273
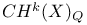 272 272
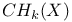 (Chow group) 272 (Chow group) 272
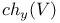 121 121
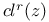 (cycle class map) 275 (cycle class map) 275
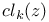 (cycle class map) 287 (cycle class map) 287
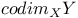 (codimension) 42 87 (codimension) 42 87
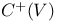 (even Clifford algebra of orthogonal space V) 303 (even Clifford algebra of orthogonal space V) 303
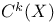 (cycle group) 61 (cycle group) 61
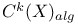 (cycles algebraically equivalent to zero) 180 (cycles algebraically equivalent to zero) 180
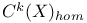 (cycles homologous to zero) 173 (cycles homologous to zero) 173
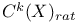 (cycles rationally equivalent to zero) 180 (cycles rationally equivalent to zero) 180
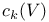 (Chern class of a vector bundle V) 106 (Chern class of a vector bundle V) 106
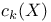 (Chern class of X) 106 (Chern class of X) 106
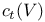 108 108
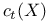 118 118
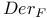 (A,A) (F-derivations from A to A) 3O2 (A,A) (F-derivations from A to A) 3O2
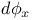 (differential of morphism (differential of morphism  at point x) 3O2 at point x) 3O2
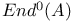 (endomorphism algebra of Abelian variety A) 306 (endomorphism algebra of Abelian variety A) 306
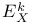 30 30
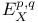 30 30
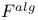 (algebraic closure of F) 299 (algebraic closure of F) 299
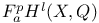 (Grothendieck’s arithmetic filtration) 87 (Grothendieck’s arithmetic filtration) 87
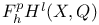 = = 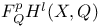 (rational Hodge filtration) 88 (rational Hodge filtration) 88
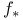 (push-forward) 172 (push-forward) 172
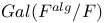 (absolute Galois group of F) 299 (absolute Galois group of F) 299
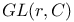 (general linear group) 17 (general linear group) 17
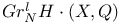 (graded piece of filtration by coniveau) 272 (graded piece of filtration by coniveau) 272
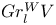 (graded piece of weight filtration) 284 (graded piece of weight filtration) 284
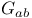 (Abelian part of reductive linear algebraic group) 300 (Abelian part of reductive linear algebraic group) 300
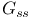 (semisimple part of reductive linear algebraic group) 300 (semisimple part of reductive linear algebraic group) 300
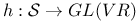 (morphism defining a Hodge structure) 310 (morphism defining a Hodge structure) 310
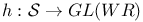 (morphism defining a complex structure) 305 (morphism defining a complex structure) 305
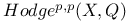 (popular version of Hodge conjecture) 88 (popular version of Hodge conjecture) 88
 (X, (X, ) 186 ) 186
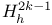 (X, (X, ) 188 ) 188
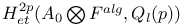 (l-adic etale cohomology of (l-adic etale cohomology of 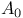 ) 348 ) 348
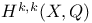 (rational Hodge classes) 63 (rational Hodge classes) 63
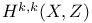 (integral Hodge classes) 60 (integral Hodge classes) 60
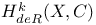 (de Rham cohomology) 31 (de Rham cohomology) 31
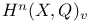 (vanishing cohomology) 206 (vanishing cohomology) 206
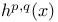 (Hodge number) 119 (Hodge number) 119
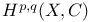 (Dolbeault cohomology) 31 (Dolbeault cohomology) 31
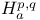 261 261
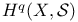 (Cech cohomology) 44 (Cech cohomology) 44
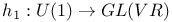 (morphism defining a Hodge structure 310 (morphism defining a Hodge structure 310
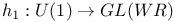 (morphism defining a complex structure) 305 (morphism defining a complex structure) 305
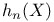 191 191
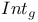 (inner automorphism by g) 302 (inner automorphism by g) 302
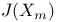 (Jacobian of (Jacobian of 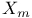 ) 320 ) 320
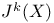 (intermediate Griffiths Jacobian) 171 (intermediate Griffiths Jacobian) 171
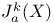 (Lieberman Jacobian) 173 (Lieberman Jacobian) 173
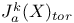 (torsion subgroup) 186 (torsion subgroup) 186
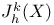 188 188
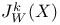 (intermediate Weil Jacobian) 171 (intermediate Weil Jacobian) 171
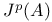 ( (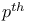 Weil intermediate Jacobian of A) 348 Weil intermediate Jacobian of A) 348
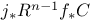 (sheaf of invariant cocycles) 229 (sheaf of invariant cocycles) 229
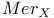 (field of meromorphic functions on X) 36 (field of meromorphic functions on X) 36
 (a set of m-tuples of integers) 320 (a set of m-tuples of integers) 320
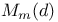 (a subset of (a subset of  ) 320 ) 320
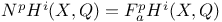 (filtration by coniveau) 272 (filtration by coniveau) 272
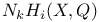 (filtration by niveau) 285 (filtration by niveau) 285
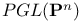 (projective general linear group) 24 (projective general linear group) 24
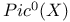 (Picard variety) 46 (Picard variety) 46
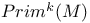 (primitive cohomology) 166 (primitive cohomology) 166
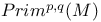 (primitive cohomology) 166 (primitive cohomology) 166
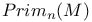 (primitive homology) 232 (primitive homology) 232
 ( (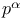 exactly divides N) 341 exactly divides N) 341
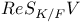 (Weil restriction of scalars functor) 299 (Weil restriction of scalars functor) 299
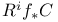 (Leray cohomology sheaf) 228 (Leray cohomology sheaf) 228
 (tangent space to G at identity e) 302 (tangent space to G at identity e) 302
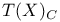 (complexified tangent bundle) 29 (complexified tangent bundle) 29
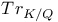 (trace from K to (trace from K to  ) 309 ) 309
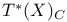 (complexified cotangent bundle) 29 (complexified cotangent bundle) 29
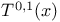 30 30
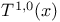 (holomorphic cotangent bundle) 18 (holomorphic cotangent bundle) 18
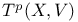 , , 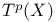 121 121
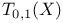 29 29
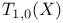 (holomorphic tangent bundle) 18 (holomorphic tangent bundle) 18
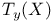 121 121
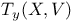 121 121
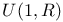 (unitary group of complex numbers of absolute value 1) 301 (unitary group of complex numbers of absolute value 1) 301
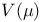 (zero set of an ideal (zero set of an ideal  ) 8 ) 8
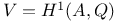 311 311
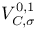 (Hodge decomposition of (Hodge decomposition of  ) 322 ) 322
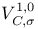 (Hodge decomposition of (Hodge decomposition of  ) 322 ) 322
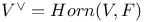 300 300
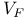 (algebraic variety or vector space over field F) 299 (algebraic variety or vector space over field F) 299
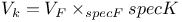 (base change from F to K) 299 (base change from F to K) 299
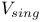 (singular set) 61 (singular set) 61
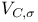 (summand of Vc where K acts via (summand of Vc where K acts via  ) 322 ) 322
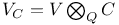 310 310
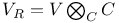 310 310
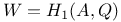 311 311
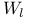 (weight filtration) 241 (weight filtration) 241
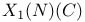 (modular curve) 330 (modular curve) 330
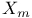 (Fermat curve of degree m) 320 (Fermat curve of degree m) 320
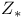 182 182
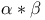 (a convolution on (a convolution on 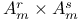 ) 319 ) 319
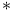 (star operator) 139 (star operator) 139
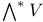 (exterior algebra of V) 304 (exterior algebra of V) 304
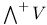 (even part of exterior algebra of V) 3O4 (even part of exterior algebra of V) 3O4
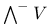 (odd part of exterior algebra of V) 3O4 (odd part of exterior algebra of V) 3O4
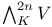 (2n exterior power of V as K-vector space) 321 (2n exterior power of V as K-vector space) 321
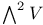 (exterior square of V) 304 (exterior square of V) 304
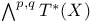 30 30
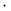 (a mod m scalar multiplication) 319 (a mod m scalar multiplication) 319
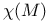 (Euler chararteristic) 193 (Euler chararteristic) 193
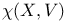 119 119
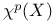 120 120
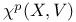 120 120
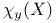 121 121
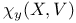 120 120
 (Laplacian) 140 (Laplacian) 140
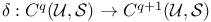 (Cech coboundary operator) 44 (Cech coboundary operator) 44
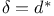 (adjoint) 140 (adjoint) 140
 (Laplacian) 142 (Laplacian) 142
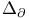 (Laplacian) 160 (Laplacian) 160
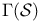 (global sections of the sheaf (global sections of the sheaf  ) 37 ) 37
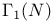 (congruence subgroup of level N) 33O (congruence subgroup of level N) 33O
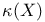 (Kodalra dimension) 269 (Kodalra dimension) 269
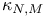 248 248
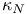 248 248
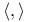 (natural pairing between V and (natural pairing between V and 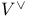 ) 300 ) 300
 (complex numbers) 1 (complex numbers) 1
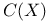 (function field of X) 8 (function field of X) 8
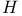 (Hamiltonian quaternion algebra) 304 (Hamiltonian quaternion algebra) 304
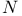 (natural numbers) 53 (natural numbers) 53
 (rational numbers) 37 (rational numbers) 37
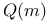 (one-dimensional rational Hodge structure of type (-m,-m)) 311 (one-dimensional rational Hodge structure of type (-m,-m)) 311
 (real numbers) 1 (real numbers) 1
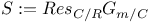 300 300
 (integers) 2 (integers) 2
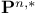 (dual projective space) 23 (dual projective space) 23
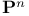 (complex projective space) 3 (complex projective space) 3
 ( ( -linear span of intersections of divisors on A) 311 -linear span of intersections of divisors on A) 311
 ( ( -linear span of p-fold intersections of divisors on A) 311 -linear span of p-fold intersections of divisors on A) 311
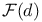 50 50
| 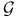 (Galois group of (Galois group of 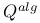 over over  ) 318 ) 318
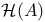 (ring of all Hodge classes on A) 311 (ring of all Hodge classes on A) 311
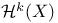 (harmonic space) 144 (harmonic space) 144
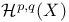 (harmonic space) 144 (harmonic space) 144
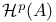 (codimension p Hodge classes on A) 311 (codimension p Hodge classes on A) 311
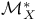 45 45
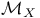 45 45
 45 45
 (ring of integers) 308 (ring of integers) 308
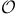 order in quaternion algebra) 309 order in quaternion algebra) 309
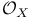 45 45
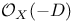 50 50
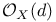 50 50
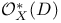 50 50
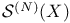 (symmetric product of X) 247 (symmetric product of X) 247
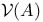 (a sum of (a sum of 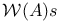 ) 323 ) 323
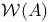 (Weil cycles on A) 321 (Weil cycles on A) 321
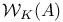 (Weil classes with respect to K) 322 (Weil classes with respect to K) 322
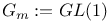 300 300
 (a set of (n+2)-tuples mod m) 319 (a set of (n+2)-tuples mod m) 319
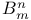 (a subset of (a subset of  ) 319 ) 319
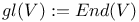 as Lie algebra 301 as Lie algebra 301
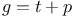 (Cartan decomposition of Lie algebra (Cartan decomposition of Lie algebra 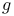 ) 303 ) 303
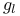 (l-adic Lie algebra) 349 (l-adic Lie algebra) 349
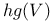 (Lie algebra of Hg(V)) 312 (Lie algebra of Hg(V)) 312
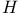 (complex upper half-plane) 330 (complex upper half-plane) 330
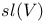 (Lie algebra of SL(V)) 303 (Lie algebra of SL(V)) 303
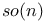 (Lie algebra of SO(n)) 303 (Lie algebra of SO(n)) 303
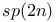 (Lie algebra of Sp(2n)) 303 (Lie algebra of Sp(2n)) 303
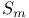 (a quotient space of (a quotient space of 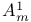 ) 320 ) 320
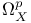 (sheaf of germs of holomorphic p-form) 30 (sheaf of germs of holomorphic p-form) 30
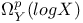 131 131
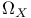 (Fano variety of lines in X) 201 (Fano variety of lines in X) 201
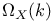 (Fano variety of k-planes on X) 218 (Fano variety of k-planes on X) 218
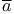 (integer congruent to a (mod m) 319 (integer congruent to a (mod m) 319
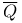 (algebraic closure of (algebraic closure of  in in  ) 283 ) 283
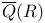 (algebraic closure of (algebraic closure of  in in  ) 213 ) 213
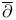 31 31
 (adjoint) 142 (adjoint) 142
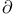 31 31
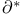 (adjoint) 160 (adjoint) 160
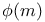 (Euler phi function) 320 (Euler phi function) 320
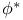 (pullback of a morphism) 302 (pullback of a morphism) 302
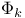 (Abel — Jacobi map) 173 (Abel — Jacobi map) 173
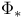 (cylinder homomorphism) 204 (cylinder homomorphism) 204
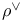 (dual representation) 300 (dual representation) 300
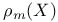 (Picard number) 207 (Picard number) 207
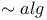 (algebraic equivalent to) 180 (algebraic equivalent to) 180
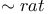 (rational equivalent to) 173 (rational equivalent to) 173
 (connection matrix) 103 (connection matrix) 103
 (curvature matrix) 104 (curvature matrix) 104
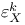 30 30
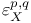 30 30
 (empty set) 8 (empty set) 8
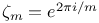 (primitive (primitive 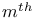 root of unity) 320 root of unity) 320
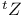 182 182
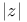 = supp z (support of z) 294 = supp z (support of z) 294
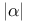 (a norm on (a norm on  ) 319 ) 319
( )’ (canonical involution on quaternion algebra) 304
(A,K) (Abelian variety of Weil type) 308
A*(X) (Chow group of cycles algebraically equivalent to zero) 181
Abel — Jacobi map 5 75 176 292
Abel — Jacobi map, analyticity 75 185
Abel — Jacobi map, functoriality properties 183
Abelian variety 12 93 259 298 299 307 314
Abelian variety, Albert classification 307
Abelian variety, algebraic family 336
Abelian variety, degenerate 339 340
Abelian variety, elliptic curve 307 329 330 342
Abelian variety, endomorphism algebra 306 348
Abelian variety, endomorphism ring 336
Abelian variety, four-dimensional 319
Abelian variety, fourfold 308 323 333 335 343 348
Abelian variety, general 310 342 343 345
Abelian variety, index of degeneracy 336
Abelian variety, level structure 336 348
Abelian variety, morphism 299
Abelian variety, nondegenerate 338 339
Abelian variety, of CM-type 309 327 329 337 339 340 349
Abelian variety, of Fermat type 319—321 334
Abelian variety, of Hodge type, family 349
Abelian variety, of prime dimension 308 326 339 345
Abelian variety, of Ribet type 308
Abelian variety, of RM-type 329
Abelian variety, of type H 330
Abelian variety, of type III 324 334
Abelian variety, of Weil type 308 319 321—323 333 334 341 349
Abelian variety, polarization 306 335 336 348 349
Abelian variety, principal polarization 14 175 343
Abelian variety, simple 306 324 326 332 333 335 336 338 344
Abelian variety, stably degenerate 335
Abelian variety, stably nondegenerate 330—332 335 342 345 348
Abelian variety, threefold 342 343
Abelian variety, with multiplication by an imaginary quadratic field 307
Abelian variety, with quaternionic multiplication 309 343
Abelian variety, with real multiplication 308
Abel’s theorem 5 83
Ad (adjoint representation of G on  ) 3O2 ) 3O2
ad (adjoint representation of Lie(G) on itself) 302
Adequate equivalence 194
Adjoint representation 302
Adjunction formula 43 357
Adjunction formula for complete intersections 43
Adjunction formula for hypersurfaces 43
Affine variety 8
Alb(X) (Albanese variety) 171
Albanese map 178
Albanese variety 171
Albert classification 307 308
Algebraic cocycle 58 189
Algebraic equivalence 84 180 194
Algebraic equivalence vs. homological equivalence 84
Algebraic group 299 301 316
Algebraic group, affine 299
Algebraic group, linear 299 300
Algebraic group, real reductive 303
Algebraic group, reductive 300 301 313
Algebraic group, semisimple 300
Algebraic torus 300 315 328 337
Almost complex structure 30
Alternating group 340
Analytic hypersurface 42
Analytic map 1 182 183
Analytic subset 11
Analytic subvariety 48
Arithmetic filtration 87 272
B(X) (standard Lefschetz conjecture) 259
Base locus 71 205
Bertini’s theorem 52 203 220
Betti number 193
Bezout’s Theorem 123 203 254
Bianchi identity 116
Bilinear form skew-symmetric 301 303 325
Bilinear form symmetric 303
Bilinear form, alternating 324 327
Bimeromorphic map 200
Birational map 200
Birationally invariance of GHC(1,n,-) 200
Bloch conjecture 254
Bloch — Beilinson filtration 273 281
Blow-up 21
Blow-up along a manifold 27
Blow-up of a point 21
Bounded symmetric domain 314 349
Branching rule 336
C(V) (Clifford algebra of orthogonal space V) 303
c(V) (total Chern class) 106
c-closed 248
c-closed dimension 248
Canonical bundle 41
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



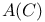 (underlying complex torus of Abelian variety A)
(underlying complex torus of Abelian variety A) 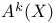
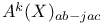 (Chow group of cycles Abel — Jacobi equivalent to zero)
(Chow group of cycles Abel — Jacobi equivalent to zero) 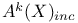 (Chow group of cycles incident equivalent to zero)
(Chow group of cycles incident equivalent to zero) 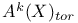 (torsion subgroup)
(torsion subgroup) 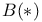 (standard Lefschetz conjecture)
(standard Lefschetz conjecture) 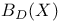 (blow-up of X along a manifold D)
(blow-up of X along a manifold D) 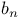 (X) (Betti number)
(X) (Betti number) 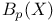 (blow-up of X at a point p)
(blow-up of X at a point p) 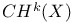 (Chow group)
(Chow group) 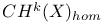 (Chow group of cycles homologous to zero)
(Chow group of cycles homologous to zero) 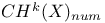 (Chow group of cycles numerically equivalent to zero)
(Chow group of cycles numerically equivalent to zero) 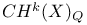
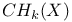 (Chow group)
(Chow group) 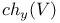
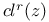 (cycle class map)
(cycle class map) 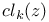 (cycle class map)
(cycle class map) 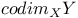 (codimension)
(codimension) 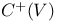 (even Clifford algebra of orthogonal space V)
(even Clifford algebra of orthogonal space V) 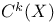 (cycle group)
(cycle group) 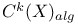 (cycles algebraically equivalent to zero)
(cycles algebraically equivalent to zero) 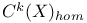 (cycles homologous to zero)
(cycles homologous to zero) 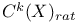 (cycles rationally equivalent to zero)
(cycles rationally equivalent to zero) 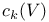 (Chern class of a vector bundle V)
(Chern class of a vector bundle V) 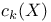 (Chern class of X)
(Chern class of X) 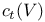
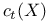
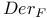 (A,A) (F-derivations from A to A)
(A,A) (F-derivations from A to A) 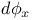 (differential of morphism
(differential of morphism  at point x)
at point x) 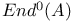 (endomorphism algebra of Abelian variety A)
(endomorphism algebra of Abelian variety A) 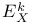
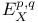
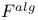 (algebraic closure of F)
(algebraic closure of F) 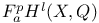 (Grothendieck’s arithmetic filtration)
(Grothendieck’s arithmetic filtration) 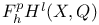 =
= 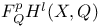 (rational Hodge filtration)
(rational Hodge filtration) 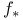 (push-forward)
(push-forward) 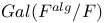 (absolute Galois group of F)
(absolute Galois group of F) 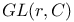 (general linear group)
(general linear group) 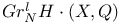 (graded piece of filtration by coniveau)
(graded piece of filtration by coniveau) 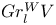 (graded piece of weight filtration)
(graded piece of weight filtration) 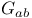 (Abelian part of reductive linear algebraic group)
(Abelian part of reductive linear algebraic group) 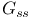 (semisimple part of reductive linear algebraic group)
(semisimple part of reductive linear algebraic group) 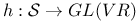 (morphism defining a Hodge structure)
(morphism defining a Hodge structure) 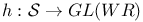 (morphism defining a complex structure)
(morphism defining a complex structure) 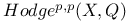 (popular version of Hodge conjecture)
(popular version of Hodge conjecture)  (X,
(X, )
) 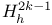 (X,
(X,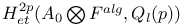 (l-adic etale cohomology of
(l-adic etale cohomology of 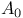 )
) 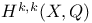 (rational Hodge classes)
(rational Hodge classes) 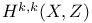 (integral Hodge classes)
(integral Hodge classes) 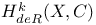 (de Rham cohomology)
(de Rham cohomology) 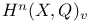 (vanishing cohomology)
(vanishing cohomology) 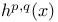 (Hodge number)
(Hodge number) 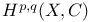 (Dolbeault cohomology)
(Dolbeault cohomology) 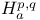
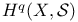 (Cech cohomology)
(Cech cohomology) 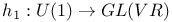 (morphism defining a Hodge structure
(morphism defining a Hodge structure 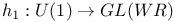 (morphism defining a complex structure)
(morphism defining a complex structure) 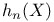
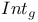 (inner automorphism by g)
(inner automorphism by g) 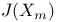 (Jacobian of
(Jacobian of 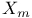 )
) 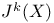 (intermediate Griffiths Jacobian)
(intermediate Griffiths Jacobian) 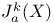 (Lieberman Jacobian)
(Lieberman Jacobian) 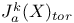 (torsion subgroup)
(torsion subgroup) 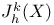
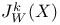 (intermediate Weil Jacobian)
(intermediate Weil Jacobian) 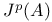 (
(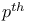 Weil intermediate Jacobian of A)
Weil intermediate Jacobian of A) 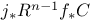 (sheaf of invariant cocycles)
(sheaf of invariant cocycles) 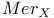 (field of meromorphic functions on X)
(field of meromorphic functions on X)  (a set of m-tuples of integers)
(a set of m-tuples of integers) 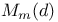 (a subset of
(a subset of 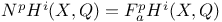 (filtration by coniveau)
(filtration by coniveau) 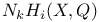 (filtration by niveau)
(filtration by niveau) 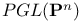 (projective general linear group)
(projective general linear group) 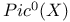 (Picard variety)
(Picard variety) 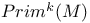 (primitive cohomology)
(primitive cohomology) 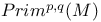 (primitive cohomology)
(primitive cohomology) 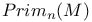 (primitive homology)
(primitive homology)  (
(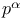 exactly divides N)
exactly divides N) 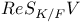 (Weil restriction of scalars functor)
(Weil restriction of scalars functor) 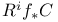 (Leray cohomology sheaf)
(Leray cohomology sheaf)  (tangent space to G at identity e)
(tangent space to G at identity e) 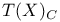 (complexified tangent bundle)
(complexified tangent bundle) 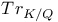 (trace from K to
(trace from K to 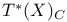 (complexified cotangent bundle)
(complexified cotangent bundle) 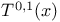
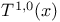 (holomorphic cotangent bundle)
(holomorphic cotangent bundle) 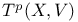 ,
, 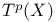
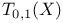
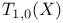 (holomorphic tangent bundle)
(holomorphic tangent bundle) 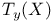
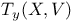
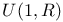 (unitary group of complex numbers of absolute value 1)
(unitary group of complex numbers of absolute value 1) 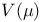 (zero set of an ideal
(zero set of an ideal  )
) 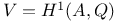
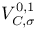 (Hodge decomposition of
(Hodge decomposition of  )
) 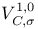 (Hodge decomposition of
(Hodge decomposition of 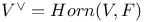
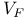 (algebraic variety or vector space over field F)
(algebraic variety or vector space over field F) 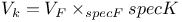 (base change from F to K)
(base change from F to K)  (singular set)
(singular set)  (summand of Vc where K acts via
(summand of Vc where K acts via  )
) 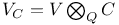
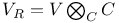
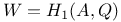
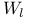 (weight filtration)
(weight filtration) 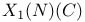 (modular curve)
(modular curve) 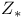
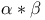 (a convolution on
(a convolution on 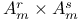 )
) 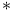 (star operator)
(star operator) 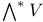 (exterior algebra of V)
(exterior algebra of V) 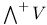 (even part of exterior algebra of V)
(even part of exterior algebra of V) 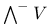 (odd part of exterior algebra of V)
(odd part of exterior algebra of V) 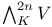 (2n exterior power of V as K-vector space)
(2n exterior power of V as K-vector space) 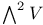 (exterior square of V)
(exterior square of V) 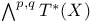
 (a mod m scalar multiplication)
(a mod m scalar multiplication) 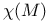 (Euler chararteristic)
(Euler chararteristic) 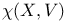
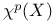
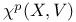
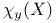
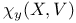
 (Laplacian)
(Laplacian) 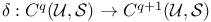 (Cech coboundary operator)
(Cech coboundary operator) 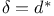 (adjoint)
(adjoint)  (Laplacian)
(Laplacian) 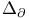 (Laplacian)
(Laplacian) 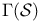 (global sections of the sheaf
(global sections of the sheaf  )
) 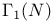 (congruence subgroup of level N)
(congruence subgroup of level N) 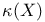 (Kodalra dimension)
(Kodalra dimension) 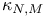
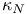
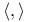 (natural pairing between V and
(natural pairing between V and 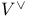 )
)  (complex numbers)
(complex numbers) 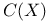 (function field of X)
(function field of X) 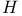 (Hamiltonian quaternion algebra)
(Hamiltonian quaternion algebra) 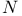 (natural numbers)
(natural numbers) 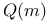 (one-dimensional rational Hodge structure of type (-m,-m))
(one-dimensional rational Hodge structure of type (-m,-m))  (real numbers)
(real numbers) 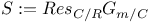
 (integers)
(integers) 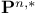 (dual projective space)
(dual projective space) 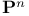 (complex projective space)
(complex projective space)  (
(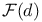
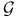 (Galois group of
(Galois group of 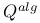 over
over 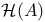 (ring of all Hodge classes on A)
(ring of all Hodge classes on A) 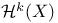 (harmonic space)
(harmonic space) 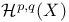 (harmonic space)
(harmonic space) 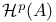 (codimension p Hodge classes on A)
(codimension p Hodge classes on A) 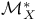
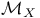
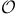
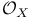
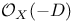
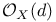
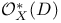
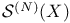 (symmetric product of X)
(symmetric product of X) 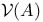 (a sum of
(a sum of 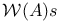 )
) 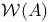 (Weil cycles on A)
(Weil cycles on A) 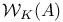 (Weil classes with respect to K)
(Weil classes with respect to K) 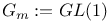
 (a set of (n+2)-tuples mod m)
(a set of (n+2)-tuples mod m) 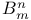 (a subset of
(a subset of 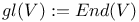 as Lie algebra
as Lie algebra 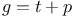 (Cartan decomposition of Lie algebra
(Cartan decomposition of Lie algebra 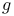 )
) 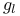 (l-adic Lie algebra)
(l-adic Lie algebra) 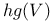 (Lie algebra of Hg(V))
(Lie algebra of Hg(V)) 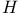 (complex upper half-plane)
(complex upper half-plane) 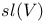 (Lie algebra of SL(V))
(Lie algebra of SL(V)) 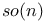 (Lie algebra of SO(n))
(Lie algebra of SO(n)) 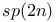 (Lie algebra of Sp(2n))
(Lie algebra of Sp(2n)) 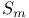 (a quotient space of
(a quotient space of 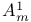 )
) 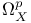 (sheaf of germs of holomorphic p-form)
(sheaf of germs of holomorphic p-form) 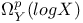
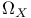 (Fano variety of lines in X)
(Fano variety of lines in X) 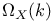 (Fano variety of k-planes on X)
(Fano variety of k-planes on X) 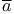 (integer congruent to a (mod m)
(integer congruent to a (mod m) 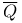 (algebraic closure of
(algebraic closure of 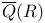 (algebraic closure of
(algebraic closure of 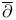
 (adjoint)
(adjoint) 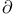
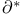 (adjoint)
(adjoint) 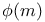 (Euler phi function)
(Euler phi function) 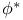 (pullback of a morphism)
(pullback of a morphism) 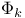 (Abel — Jacobi map)
(Abel — Jacobi map) 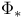 (cylinder homomorphism)
(cylinder homomorphism) 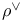 (dual representation)
(dual representation) 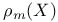 (Picard number)
(Picard number) 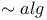 (algebraic equivalent to)
(algebraic equivalent to) 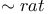 (rational equivalent to)
(rational equivalent to)  (connection matrix)
(connection matrix)  (curvature matrix)
(curvature matrix) 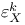
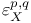
 (empty set)
(empty set) 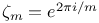 (primitive
(primitive 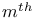 root of unity)
root of unity) 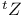
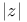 = supp z (support of z)
= supp z (support of z) 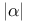 (a norm on
(a norm on