|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Simon B. — Quantum mechanics for Hamiltonians defined as quadratic forms |
|
|
 |
| Предметный указатель |
 -classes viii -classes viii
Approximation theorems, bound states 88—89
Approximation theorems, propagators 48
Approximation theorems, resolvants 48
Approximation theorems, S-matrices 112
Approximation theorems, spectral projections 48
Approximation theorems, wave operators 112
Asymptotic completeness 99 129
Asymptotic completeness, weak 99 105—110
Bargmann's bounds 89
Born series 15—22
Bound states, asymptotic behavior in 79 154—155
Bound states, bounds on the number of 85—89
Canonically cut plane 47
Closed operator 205
Cluster decomposition 180
Compact operators 217
Completeness of the wave operators 99 105—110 141
Contour pinching 168—171
Convergence, norm (operator) 202
Convergence, norm (vector) 202
Convergence, strong (operator) 202
Convergence, weak (operator) 203
Convergence, weak (vector) 202
Cook's theorem 102
Core see domains of essential self-adjointness
Dispersion relations, forward 152—154
Dispersion relations, non-forward 159—160
Domains of essential self-adjointness 49 205
Eigenfunction expansions 115—126 133—135 138—143
Feynman path integral 50—53
Finite range potentials 24—26 130 155—173
Fredholm theorem, analytic 218
Ghirardi — Rimini bound 88—89
Green's function 72—77 118—120
Green's function, disconnected part 178—179
Green's function, reduced 184
Hack's theorem 103
Helium atom 194—196
Hilbert — Schmidt operators 220
Hughes — Eckart terms 190—194
Hunziker's theorem 185—186
Ikebe's theory see eigenfunction expansions
Integral equation, bound state 79 80—85
Integral equation, factorized 20—21 148
Integral equation, Lippmann — Schwinger 117
Interpolation theorem, Hunt's 10
| Interpolation theorem, Marcinkiewicz 9
Kato — Birman theorem 105—106
Kato — Rellich perturbation theory 69
Kato — Rellich theorem 206
Kato's theorem 32
Khuri conditions 147
Kisynski's theorems 56
Klein — Zemach theorem 23—24 95 1
KLMN theorem 41
Kupsch — Sandas theorem 104
Kuroda's approximation theorem 11
Legendre series, convergence of 162—165
Lehmann ellipse 160—161
Multiparticle Hamiltonian, definition of 174
Non-nasty potentials 6 18 36 147
Partial waves, analyticity of 163
Quadratic forms 33 38—45 215
refinement 181
Rollnik classes 3
Rollnik norm, 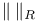 3 3
Scale of spaces see quadratic forms
Schwinger's bound 86—87
Self adjoint operator 204
Self adjoint operator, essentially 205
Sobolev inequalities 4 9—12
Sobolev spaces see quadratic forms
Spectral projections 213
Spectral theorem 207 213
Spectrum 208
Spectrum, absolutely continuous 210—211
Spectrum, discrete 214
Spectrum, essential 215
Spectrum, pure point 210—211
Spectrum, singular 101 130 210—211
Stone's theorem 216
String 181
T-matrix 143 152
Tiktopoulos' formula 45 47 175
Trace class 220
Trotter — Kato theorem 217
Trotter's theorem 217
Unitary propagator 53
Wave operators 94 97—99 102—110
Wave operators, Dollard 110
Weinberg — Van Winter expansion 175—179
Weinberg — Van Winter expansion, factorized 179—185
Weyl's min-max principle 71
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -classes
-classes