|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Luke Y.L. Ч The special functions and their approximations (volume 1) |
|
|
 |
| ѕредметный указатель |
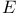 Ч Function 148 Ч Function 148
 -Function see Chapter V (135Ч208) -Function see Chapter V (135Ч208)
 -Function, analytic continuation 148 149 194 -Function, analytic continuation 148 149 194
 -Function, asymptotic expansion, exponential, recurrence formula for coefficients in 200 202 205Ч208 -Function, asymptotic expansion, exponential, recurrence formula for coefficients in 200 202 205Ч208
 -Function, asymptotic expansion, large variable 178Ч180 189Ч194 -Function, asymptotic expansion, large variable 178Ч180 189Ч194
 -Function, definition 139 142Ч145 -Function, definition 139 142Ч145
 -Function, differential equation and solutions 181 182 -Function, differential equation and solutions 181 182
 -Function, elementary properties 149Ч152 -Function, elementary properties 149Ч152
 -Function, expansion of in series of -Function, expansion of in series of  -functions 147 148 152Ч157 183Ч189 -functions 147 148 152Ч157 183Ч189
 -Function, expansion of in series of generalized hypergeometric functions 139 142 145Ч147 -Function, expansion of in series of generalized hypergeometric functions 139 142 145Ч147
 -Function, hypergeometric functions and named functions, connection with 225Ч234 -Function, hypergeometric functions and named functions, connection with 225Ч234
 -Function, integral representations 59 143Ч145 159 164 175 177 -Function, integral representations 59 143Ч145 159 164 175 177
 -Function, integrals involving, Euler and related transforms 170Ч177 -Function, integrals involving, Euler and related transforms 170Ч177
 -Function, integrals involving, Founer transform 166 169 -Function, integrals involving, Founer transform 166 169
 -Function, integrals involving, Laplace and inverse Laplace transforms 166Ч169 -Function, integrals involving, Laplace and inverse Laplace transforms 166Ч169
 -Function, integrals involving, Mellin and inverse Mellin transforms 157Ч159 -Function, integrals involving, Mellin and inverse Mellin transforms 157Ч159
 -Function, integrals involving, other transform pairs 177 -Function, integrals involving, other transform pairs 177
 -Function, integrals involving, product of two -Function, integrals involving, product of two  -functions 159 166 -functions 159 166
 -Function, multiplication theorems 152Ч157 -Function, multiplication theorems 152Ч157
 -Function, named functions expressed in terms of 225Ч230 -Function, named functions expressed in terms of 225Ч230
 -functions; special cases of -functions; special cases of  Hypergeometric function (generalized), Hypergeometric function (generalized),  , analytic continuation 149 , analytic continuation 149
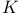 Ч Transform 165 Ч Transform 165
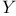 Ч Transform 165 Ч Transform 165
 -function see Hypergeometric function (confluent) Whittaker -function see Hypergeometric function (confluent) Whittaker
Airy functions 205 217
Anger function 218
Approximation, best in Chebyshev sense 303 305
Approximation, best in least square sense 270
Approximation, best in mean square sense 268 305
Associated Bessel function 219
Asymptotic expansion see Chapter I 1-7; asymptotic
Asymptotic expansion, definition 2
Asymptotic expansion, elementary properties 3 4
Asymptotic expansion, WatsonТs lemma 4 7
Basic series 291
Ber and Bei functions 216
Bernoulli and generalized Bernoulli polynomials, definition and elementary properties 18Ч22
Bernoulli and generalized Bernoulli polynomials, Fourier series for 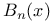 23 23
Bernoulli and generalized Bernoulli polynomials, integrals of 22 23
Bernoulli and generalized Bernoulli polynomials, recurrence formulas 20 22 35
Bernoulli and generalized Bernoulli polynomials, table of 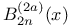 34 34
Bernoulli and generalized Bernoulli polynomials, table of 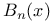 20 20
Bernoulli and generalized Bernoulli polynomials, table of 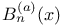 19 19
Bernoulli numbers, definition 19
Bernoulli numbers, expansion of cot z, tan z, csc z, and ln cos z in series involving 23
Bernoulli numbers, table of 20
Bessel functions,  -functions, connection with 226Ч233 -functions, connection with 226Ч233
Bessel functions, associated 219
Bessel functions, asymptotic expansions 204 215
Bessel functions, confluent hypergeometric function, connection with 120 135 213
Bessel functions, definitions, connecting relations, power series 39 40 212 213
Bessel functions, derivatives with respect to order at half an odd integer 216
Bessel functions, difference-differential properties 48 214
Bessel functions, differential equation 120 214
Bessel functions, expansion of exponential function in series of 287
Bessel functions, integrals involving 115 165 177 219 220 287
Bessel functions, Jacobi polynomial, connection with 52
Bessel functions, products 216 228Ч230 232Ч234
Bessel functions, Wronskians 214 215
Bessel functions, zeros of 205
Bessel polynomials 274
Beta function, complete 15 16 18
Beta function, incomplete 210
Beta transform 58 59 170Ч175 286
Binomial coefficient 9 35
Binomial function 38 40 49 209 210
Chebyshev polynomials of first kind see also Jacobi polynomials
Chebyshev polynomials of first kind, approximations in series of (based on orthogonality properties with respect to summation) 308 312
Chebyshev polynomials of first kind, definition and basic properties 273 296 297 300 301
Chebyshev polynomials of first kind, difference-differential properties 297Ч299 301 302 316 321 324
Chebyshev polynomials of first kind, evaluation of series of, by use of backward recurrence formula 325Ч329
Chebyshev polynomials of first kind, expansion of 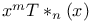 in series of 301 in series of 301
Chebyshev polynomials of first kind, expansion of 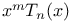 in series of 298 in series of 298
Chebyshev polynomials of first kind, expansion of a 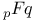 in series of 296 in series of 296
Chebyshev polynomials of first kind, expansions in series of (based on orthogonality property with respect to integration), asymptotic estimate of coefficients 293Ч296
Chebyshev polynomials of first kind, expansions in series of (based on orthogonality property with respect to integration),differential and integral properties 314Ч325
Chebyshev polynomials of first kind, expansions in series of (based on orthogonality property with respect to integration),evaluation of coefficients 286Ч293
Chebyshev polynomials of first kind, integrals involving 293Ч295 299 300Ч302 316-325
Chebyshev polynomials of first kind, Jacobi polynomial, connection with 273 296
Chebyshev polynomials of first kind, minimax and mean square properties 303Ч307
Chebyshev polynomials of first kind, orthogonality property with respect to integration 273 299 301
Chebyshev polynomials of first kind, orthogonality property with respect to summation 307 310 311
Chebyshev polynomials of second kind see also Jacobi polynomials
Chebyshev polynomials of second kind, approximations in series of (based on orthogonality properties with respect to summation) 312Ч314
Chebyshev polynomials of second kind, definition and basic properties 273 296Ч300
Chebyshev polynomials of second kind, integrals involving 299 300
Chebyshev polynomials of second kind, Jacobi polynomial, connection with 273
Chebyshev polynomials of second kind, orthogonality property with respect to integration 299
Chebyshev polynomials of second kind, orthogonality property with respect to summation 312 313
Chebyshev, best approximation in sense of 303
Christoffel Ч Darboux formulas 272
Confluence principle and theorems 48Ч57
Confluent hypergeometric function see Hypergeometric function (confluent)
Cosecant 23 210
Cosine 23 39 210
Cosine integral 135 221Ч223 227
Cotangent 23
Coulomb wave functions 135 212
Cylinder function 204 213
D operator 24Ч26
Darboux, method of generating functions 254Ч259
Delta ( ) operator 24 26 ) operator 24 26
Difference equations, use of in backward direction 317Ч319 325Ч329
DixonТs theorem 103 104
Elliptic integrals 211
Error functions 135 223 224
Euler Ч Mascheroni constant, y 9
Expansions see also Particular functions evaluation of in
Expansions, difference equation 325Ч329
Exponential function 38 40 48 209 287 288
Exponential integral 3 7 135 221 222
Fresnel integrals 135 224 227
Gamma function see Chapter II (8Ч37)
Gamma function, asymptotic expansion, 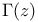 and ln and ln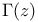 31Ч33 31Ч33
Gamma function, asymptotic expansion, ratio of products of gamma functions 33Ч37
Gamma function, asymptotic expansion, recurrence formula for coefficients in asymptotic expansion for ratio of products of gamma functions 205Ч208
Gamma function, definite integrals expressed in terms of 15 16 60 61 157 177
Gamma function, definition and elementary properties 8Ч10
Gamma function, expansion for 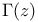 and ln and ln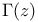 in series of Chebyshev polynomials of first kind 28 29 in series of Chebyshev polynomials of first kind 28 29
Gamma function, integral representations 8 14 18
Gamma function, logarithmic derivative of see Psi-function
Gamma function, multiplication formula 11Ч12
Gamma function, power series and other expansions 26 31
Gegenbauer polynomial 273 279
H Ч Transform 165
Hankel functions 135 204 213 215 230 234
Hankel transform 165 287
Hermite polynomials 135 273
Hypergeometric function (confluent),  , ,  -function, Whittaker functions see Chapter IV (115Ч134) Hypergeometric -function, Whittaker functions see Chapter IV (115Ч134) Hypergeometric
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, -function, Whittaker functions,  -function, connection with 225 226 228 231 234 -function, connection with 225 226 228 231 234
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, asymptotic expansion, large variable 127 128 -function, Whittaker functions, asymptotic expansion, large variable 127 128
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, confluence principle 48 -function, Whittaker functions, confluence principle 48
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, contiguous relations 48 118 119 126 -function, Whittaker functions, contiguous relations 48 118 119 126
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, definition 40 47 49 -function, Whittaker functions, definition 40 47 49
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, difference-differential properties 48 117Ч119 125 126 -function, Whittaker functions, difference-differential properties 48 117Ч119 125 126
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, differential equation 119 120 -function, Whittaker functions, differential equation 119 120
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, differential equation, solutions, complete 121Ч124 -function, Whittaker functions, differential equation, solutions, complete 121Ч124
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, differential equation, solutions, degenerate 120 121 -function, Whittaker functions, differential equation, solutions, degenerate 120 121
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, differential equation, solutions, logarithmic 122 123 -function, Whittaker functions, differential equation, solutions, logarithmic 122 123
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, differential equation, solutions, ordinary 119 -function, Whittaker functions, differential equation, solutions, ordinary 119
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, elementary relations 117 118 -function, Whittaker functions, elementary relations 117 118
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, evaluation of certain -function, Whittaker functions, evaluation of certain  for special value of argument 113 for special value of argument 113
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, expansion in series of Bessel functions 129Ч133 -function, Whittaker functions, expansion in series of Bessel functions 129Ч133
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, expressed as named function 224 -function, Whittaker functions, expressed as named function 224
| Hypergeometric function (confluent),  , ,  -function, Whittaker functions, integral representations 115Ч117 -function, Whittaker functions, integral representations 115Ч117
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, Kummer relations 121 124 126 -function, Whittaker functions, Kummer relations 121 124 126
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, named functions expressed in terms of 211Ч213 220Ч223 -function, Whittaker functions, named functions expressed in terms of 211Ч213 220Ч223
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, other notations and related functions 134 135 -function, Whittaker functions, other notations and related functions 134 135
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, products 211 228 233 234 -function, Whittaker functions, products 211 228 233 234
Hypergeometric function (confluent),  , ,  -function, Whittaker functions, Wronskians 124 -function, Whittaker functions, Wronskians 124
Hypergeometric function (Gaussian),  see Chapter III (38Ч114) Hypergeometric function (generalized) see Chapter III (38Ч114) Hypergeometric function (generalized)
Hypergeometric function (Gaussian),  , ,  -function, connection with 139 -function, connection with 139
Hypergeometric function (Gaussian),  , analytic continuation 68Ч71 , analytic continuation 68Ч71
Hypergeometric function (Gaussian),  , asymptotic expansions for large parameters) 235Ч242 , asymptotic expansions for large parameters) 235Ч242
Hypergeometric function (Gaussian),  , confluence principle 49 , confluence principle 49
Hypergeometric function (Gaussian),  , contiguous relations 47 89 , contiguous relations 47 89
Hypergeometric function (Gaussian),  , convergence of series 65 68 , convergence of series 65 68
Hypergeometric function (Gaussian),  , definition 39 41 , definition 39 41
Hypergeometric function (Gaussian),  , difference-differential properties 44Ч47 88 275 276 , difference-differential properties 44Ч47 88 275 276
Hypergeometric function (Gaussian),  , differential equation 64 93 , differential equation 64 93
Hypergeometric function (Gaussian),  , differential equation, solutions, complete 65 72Ч84 , differential equation, solutions, complete 65 72Ч84
Hypergeometric function (Gaussian),  , differential equation, solutions, degenerate 65 66 69 77 84 , differential equation, solutions, degenerate 65 66 69 77 84
Hypergeometric function (Gaussian),  , differential equation, solutions, logarithmic 75Ч84 , differential equation, solutions, logarithmic 75Ч84
Hypergeometric function (Gaussian),  , differential equation, solutions, ordinary 64 65 67Ч71 , differential equation, solutions, ordinary 64 65 67Ч71
Hypergeometric function (Gaussian),  , elementary relations 44Ч46 , elementary relations 44Ч46
Hypergeometric function (Gaussian),  , evaluation of, for special values of argument 99Ч103 114 , evaluation of, for special values of argument 99Ч103 114
Hypergeometric function (Gaussian),  , expansion in series of , expansion in series of  Тs 130 Тs 130
Hypergeometric function (Gaussian),  , expressed as named function 224 , expressed as named function 224
Hypergeometric function (Gaussian),  , integral representations 57 58 62 63 89Ч91 , integral representations 57 58 62 63 89Ч91
Hypergeometric function (Gaussian),  , integrals involving 170 172Ч174 , integrals involving 170 172Ч174
Hypergeometric function (Gaussian),  , Kummer relations 67 68 85Ч92 , Kummer relations 67 68 85Ч92
Hypergeometric function (Gaussian),  , named functions expressed in terms of 209Ч211 , named functions expressed in terms of 209Ч211
Hypergeometric function (Gaussian),  , polynomial 40 , polynomial 40
Hypergeometric function (Gaussian),  , quadratic transformations 92Ч98 , quadratic transformations 92Ч98
Hypergeometric function (Gaussian),  , truncated series 42 109 110 , truncated series 42 109 110
Hypergeometric function (Gaussian),  , Wronskians 84 , Wronskians 84
Hypergeometric function (generalized),  see Chapters III (38Ч114) IV V see Chapters III (38Ч114) IV V
Hypergeometric function (generalized),  , ,  -function, connection with 139 142 145Ч147 225 230 231 -function, connection with 139 142 145Ч147 225 230 231
Hypergeometric function (generalized),  , asymptotic expansion, exponential, recurrence formula for coefficients in 200 202 205 208 , asymptotic expansion, exponential, recurrence formula for coefficients in 200 202 205 208
Hypergeometric function (generalized),  , asymptotic expansion, large parameter(s) 51 55 56 133 242Ч266 , asymptotic expansion, large parameter(s) 51 55 56 133 242Ч266
Hypergeometric function (generalized),  , asymptotic expansion, large variable 195Ч203 , asymptotic expansion, large variable 195Ч203
Hypergeometric function (generalized),  , confluence principle and theorems 49 51 53Ч56 , confluence principle and theorems 49 51 53Ч56
Hypergeometric function (generalized),  , contiguous relations 48 , contiguous relations 48
Hypergeometric function (generalized),  , convergence of series 43 44 , convergence of series 43 44
Hypergeometric function (generalized),  , definition 41 42 136 , definition 41 42 136
Hypergeometric function (generalized),  , difference-differential properties 44 48 , difference-differential properties 44 48
Hypergeometric function (generalized),  , differential equation 136 138 247 , differential equation 136 138 247
Hypergeometric function (generalized),  , differential equation, solutions, complete 147 148 , differential equation, solutions, complete 147 148
Hypergeometric function (generalized),  , differential equation, solutions, logarithmic 140Ч143 , differential equation, solutions, logarithmic 140Ч143
Hypergeometric function (generalized),  , differential equation, solutions, ordinary 137Ч139 , differential equation, solutions, ordinary 137Ч139
Hypergeometric function (generalized),  , elementary relations 44 , elementary relations 44
Hypergeometric function (generalized),  , evaluation of , evaluation of 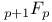 for special values of argument, for special values of argument, 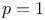 99 101 102 114 99 101 102 114
Hypergeometric function (generalized),  , evaluation of , evaluation of 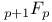 for special values of argument, for special values of argument, 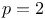 103Ч111 113 259 103Ч111 113 259
Hypergeometric function (generalized),  , evaluation of , evaluation of 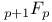 for special values of argument, for special values of argument, 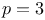 112Ч114 112Ч114
Hypergeometric function (generalized),  , evaluation of , evaluation of 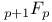 for special values of argument, general p 26 113 114 257Ч259 for special values of argument, general p 26 113 114 257Ч259
Hypergeometric function (generalized),  , evaluation of certain , evaluation of certain 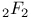 for special values of argument 113 for special values of argument 113
Hypergeometric function (generalized),  , expansion in series of Chebyshev polynomials of first kind 296 , expansion in series of Chebyshev polynomials of first kind 296
Hypergeometric function (generalized),  , expansion theorem for large parameter 51 55 56 , expansion theorem for large parameter 51 55 56
Hypergeometric function (generalized),  , expressed as named function 224 225 , expressed as named function 224 225
Hypergeometric function (generalized),  , integral representations 58 63 , integral representations 58 63
Hypergeometric function (generalized),  , integrals involving 58Ч62 164 168 169 , integrals involving 58Ч62 164 168 169
Hypergeometric function (generalized),  , multiplication theorem 155 , multiplication theorem 155
Hypergeometric function (generalized),  , named functions expressed in terms of 209Ч224 , named functions expressed in terms of 209Ч224
Hypergeometric function (generalized),  , nearly poised 103 , nearly poised 103
Hypergeometric function (generalized),  , polynomial 42 , polynomial 42
Hypergeometric function (generalized),  , truncated series 42 210 , truncated series 42 210
Hypergeometric function (generalized),  , well poised 103 104 , well poised 103 104
Incomplete gamma function and related functions 38 40 135 220Ч224
Incomplete gamma function and related functions Hypergeometric function (confluent),  , ,  -function, Whittaker functions, asymptotic expansion, large parameter(s) 129 133 134 -function, Whittaker functions, asymptotic expansion, large parameter(s) 129 133 134
Incomplete gamma function Gamma function, analytic continuation 10 11
Integrals see appropriate modifiers such as Bessel functions integrals
Jacobi function 274
Jacobi polynomials, asymptotic expansion for large order 53 54 237 250Ч259 278 279
Jacobi polynomials, Bessel function, connection with 52
Jacobi polynomials, Chebyshev polynomials Orthogonal polynomials, classical, orthogonal properties of 273
Jacobi polynomials, definition and basic properties 273Ч 275 280
Jacobi polynomials, difference-differential properties 275 276
Jacobi polynomials, evaluation and estimation of coefficients of given 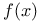 when expanded in series of 286 296 when expanded in series of 286 296
Jacobi polynomials, evaluation and estimation of coefficients of given 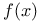 when expanded in series of, asymptotic estimates of coefficients 293 when expanded in series of, asymptotic estimates of coefficients 293
Jacobi polynomials, evaluation and estimation of coefficients of given 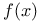 when expanded in series of, coefficients as integral transform 286Ч290 when expanded in series of, coefficients as integral transform 286Ч290
Jacobi polynomials, evaluation and estimation of coefficients of given 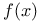 when expanded in series of, coefficients, when f(x) is defined by Taylor series 290Ч293 when expanded in series of, coefficients, when f(x) is defined by Taylor series 290Ч293
Jacobi polynomials, expansion of 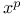 in series of 277 284 285 291 in series of 277 284 285 291
Jacobi polynomials, expansion of 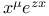 in series of 285 287 in series of 285 287
Jacobi polynomials, expansion of functions in series of 283Ч286 290Ч293
Jacobi polynomials, extended and generalized, asymptotic expansion for large order 53 54 247Ч263 281Ч283
Jacobi polynomials, extended and generalized, definition 247
Jacobi polynomials, extended and generalized, expansion of functions in series of 291
Jacobi polynomials, extended and generalized, generating function 254
Jacobi polynomials, generating functions 254 278
Jacobi polynomials, inequalities 280
Jacobi polynomials, integrals involving 276Ч277 281 282 286
Jacobi polynomials, orthogonal polynomials, connection with other 273
Jacobi polynomials, orthogonality property 276
Ker and Kei functions 216
Kontorovich Ч Lebedev transforms 177
Laguerre polynomial, asymptotic expansion for large order 264Ч265
Laguerre polynomial, confluent hypergeometric function, connection with 135
Laguerre polynomial, definition and orthogonality property 273
Laguerre polynomial, expansion of functions in series of 291 292
Laguerre polynomial, generalized and extended, asymptotic expansion for large order 263Ч266
Laguerre polynomial, generalized and extended, definition 263
Laguerre polynomial, generalized and extended, expansion of functions in series of 291 292
Laguerre polynomial, Jacobi polynomial, connection with 273
Legendre functions 178 211
Legendre polynomials 273 279
Logarithm 38 40 210
Lommel functions 217 227 234
Mehler transforms 178
Named functions expressed as  -functions 225Ч230 -functions 225Ч230
Named functions expressed as  -functions, as -functions, as  's 209Ч224 's 209Ч224
Order symbols 1
Orthogonal functions 267Ч270
Orthogonal polynomials see Chapter VIII (267Ч329)
Orthogonal polynomials, definition and basic properties 267Ч272
Parabolic cylinder functions 135 212
Pi ( ), asymptotic expansion for 35 36 ), asymptotic expansion for 35 36
Polynomials see modifiers such as Bessel orthogonal
Psi ( )-function or logarithmic derivative of the gamma function, asymptotic expansion 33 )-function or logarithmic derivative of the gamma function, asymptotic expansion 33
Psi ( )-function or logarithmic derivative of the gamma function, definition and elementary properties 12 13 )-function or logarithmic derivative of the gamma function, definition and elementary properties 12 13
Psi ( )-function or logarithmic derivative of the gamma function, expansion Psi ( )-function or logarithmic derivative of the gamma function, expansion Psi ( )-function or logarithmic derivative of the gamma function, in series of Chebyshev polynomials of the first kind 28 29 )-function or logarithmic derivative of the gamma function, in series of Chebyshev polynomials of the first kind 28 29
Psi ( )-function or logarithmic derivative of the gamma function, integral representations 13Ч15 28 )-function or logarithmic derivative of the gamma function, integral representations 13Ч15 28
Psi ( )-function or logarithmic derivative of the gamma function, power series expansion 26 )-function or logarithmic derivative of the gamma function, power series expansion 26
Recurrence formulas, use of in backward direction 317Ч319 325Ч329
RummerТs formula 57
RummerТs solutions 67
Saalsch tzТs formula 103 tzТs formula 103
Sine 39 210
Sine integral 135 221Ч223 227
Sine, inverse of 210
Stokes phenomenon 128 199
Struve functions, asymptotic expansion 219
Struve functions, definition 217
Struve functions, difference-differential properties 218
Struve functions, expressed as  -function 227 233 -function 227 233
Struve functions, integrals involving 165 220
Tangent 23
Tangent, inverse of or arc tan 38 40 210
Ultraspherical polynomial 273 279
VandermondeТs theorem 99
WatsonТs formula 104
WatsonТs lemma 4Ч7
Weber function 218
WhippleТs formula 104
Whittaker functions see also Hypergeometric function confluent
Whittaker functions, definition 134
Whittaker functions, expressed as  -function 225 226 228 231 233 234 -function 225 226 228 231 233 234
Wronskians 84 124
Zeta-function (Riemann) 27
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



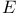 Ч Function
Ч Function  -Function
-Function  Hypergeometric function (generalized),
Hypergeometric function (generalized), 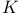 Ч Transform
Ч Transform 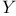 Ч Transform
Ч Transform  -function
-function 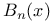
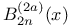
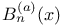
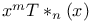 in series of
in series of 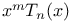 in series of
in series of 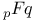 in series of
in series of  ) operator
) operator 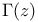 and ln
and ln ,
, 
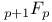 for special values of argument,
for special values of argument, 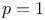
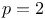
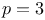
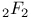 for special values of argument
for special values of argument 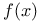 when expanded in series of
when expanded in series of 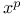 in series of
in series of 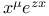 in series of
in series of  ), asymptotic expansion for
), asymptotic expansion for  tzТs formula
tzТs formula