|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Muller J.-M. — Elementary functions: algorithms and implementation |
|
|
 |
| Предметный указатель |
Accurate tables method 58
Adaptation of coefficients 43
Addition 13
Agarwal 2 163
AMD K5 48
Antelo 124
Arithmetic-geometric mean 173 181
Avizienis' algorithm 14 15
Bailey 181
Baker's predictive algorithm 90
Base 9
BKM, algorithm 131
BKM, E-mode 133
BKM, iteration 133
BKM, L-mode 133 137
Bogacki 124
Borrow-save, addition 16
Borrow-save, number system 16
Branching cordic algorithm 115
Braune 47
Brent 173 181
Briggs 4 71 72
Carry propagation 13
Carry-save, addition 16
Carry-save, computation of exponentials 86
Carry-save, number system 15 82 111
Cavallaro 125
CELEFUNT 48
chebyshev 30
Chebyshev approximation to 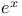 26 26
Chebyshev approximation to functions 23
Chebyshev polynomials 23 26
Chebyshev theorem 25 26
Chebyshev theorem for rational approximations 34
Cody 1 48 147
Complex arguments 48
Continued fractions 149
CoRDIC 5 76 101
CORDIC on line 125
CORDIC, arcos 122
CORDIC, arcsin 122
CORDIC, branching 115
CORDIC, decimal 124
CORDIC, differential 118—120
CORDIC, double rotation 112
CORDIC, hyperbolic mode 105
CORDIC, iteration 105
CORDIC, rotation mode 102 106
CORDIC, scale factor compensation 107
CORDIC, vectoring mode 105 106
Correct rounding 2 163
Cyrix, 83D87 62
Cyrix, FastMath 41
Daggett 124
Dawid and Meyr 118
Delosme 112 124
DeLugish 98
Deprettere 109 125
Despain 107
Dewilde 109
Differential CORDIC 118—120
Discrete base 76 102
Distillation 12
Double rotation method 112
Dunham 39
E-method 45
Ercegovac 3 119 125 174
Ercegovac, E-method 45
Ercegovac, radix-16 algorithms 127
Exact rounding 2 12 165
Exceptions 12 175—177
Exponential, Baker's method 97
Exponential, BKM 133
Exponential, fast shift and add algorithm 81
Exponential, multiple precision 181 182
Exponential, radix-16 127
Exponential, restoring algorithm 73 77
Exponential, table-driven 55
Exponential, Tang 55
Exponential, Wong and Goto 65
Feldstein 169
Final rounding 163
Floating-point arithmetic 9—13
Floating-point arithmetic, test of 13
floating-point division 35
Flynn 35
Fourier transform 101
Fused MAC 43
Gal, accurate tables method 58
Goldberg 9
Goodman 169
Gradual underflow 12
Hamada 36
Hanek 147
Hartley transform 101
Haviland 107
Hekstra 125
Hemkumar 125
Hewlett Packard's HP 35 101
High-radix algorithms 127
Horner's scheme 43
Hsiao 124
hu 124 125
IBM/370 58
IEEE-754 standard 1 10—12 62 175
infinity 12
Intel, 8087 1 9 101 124
Intel, Pentium 15
Interval arguments 48
Interval arithmetic 12
Jacobi approximation to functions 23
Jacobi polynomials 23
Kahan 1 9 147 149 176
Koren 3 35
Kota 125
Kramer 47
Krishnamurthy 76
Kropa 124
Kuki 1
Lang 3 125 174
Least maximum approximation to 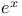 26 26
Least maximum approximation to functions 24
Least squares approximations 22
Legendre approximation to 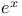 25 25
Legendre approximation to functions 23
Legendre polynomials 23 25
| Lin 125
Lindemann theorem 167
Linhardt 98
Litvinov 34
Logarithm, BKM 137
Logarithm, fast shift and add algorithm 88
Logarithm, multiple precision 181 182
Logarithm, restoring algorithm 79 80
Logarithm, table-driven 57
Logarithm, Tang 57
Logarithm, Wong and Goto 62
Luk 125
Lynch 175
MACHAR 13
Malcolm 13
Maple 2 38
Meggitt 76 98
Miller 98
Minimax approximation to 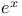 26 26
Minimax approximations 24
Modular range reduction 158
Monotonicity 2 163 164
Motorola, 68881 124
Motorola, Power PC 43
Multiple precision 147 180
Multiple precision, exponentials 181 182
Multiple precision, logarithms 181
Naganathan 124
Nan (not a number) 12 176
Nesterenko 172
Nonrestoring algorithm 76 102
Normalized numbers 10
Oberman 35
Okabe 1
Omondi 3
Orthogonal polynomials 22
Pade approximants 35
Paranoia 13
Payne 147
Pocket calculators 10 101 124
Polynomial approximations 21—25 29 31 35
Polynomial approximations, least maximum 24
Polynomial approximations, least squares 22
Polynomial approximations, particular form 39
Polynomial approximations, speed of convergence 31
Polynomial evaluation 43
Polynomial evaluation, adaptation of coefficients 43
Polynomial evaluation, E-method 45
Polynomial evaluation, Estrin's method 47
Polynomial evaluation, Horner's scheme 43
Polynomier 47
Power function 178
Predictive algorithm 90
Pseudodivision 76 98
Pseudomultiplication 76 98
RADIX 9
Radix-16 algorithms 127
Range limits 2 163
Range reduction 5 56 143—149 152—154 156 158 176
Range reduction, additive 143
Range reduction, Cody and Waite 148
Range reduction, modular 158
Range reduction, multiplicative 143
Range reduction, Payne and Hanek 154
Range reduction, positive 158
Range reduction, redundant 158
Range reduction, symmetrical 158
Range reduction, Tang 56
Range reduction, worst cases 149
Rational approximations 34—36
Rational approximations, equivalent expressions 36
Rational approximations, particular form 39
Reduced argument 143
Redundant number systems 13 15 81 82 88 95 109 111 112 114 115 131 161
remez 34
Restoring algorithm 74
Robertson diagrams 82 83 88 109 128 134 135
Rounding modes 10—12 165 166
Salamin 181
Sarkar 76
Scale factor compensation 107
Schmid 124
Schulte and Swartzlander 168
Shift-and-add, algorithms 71 73 76 81 88 98 101 127
Shift-and-add, exponentials in a redundant number system 81
Shift-and-add, logarithms in a redundant number system 88
Signed zeroes 12
Signed-digit, computation of exponentials 83
Signed-digit, number system 14 15 82 111
Sine and cosine, accurate tables 60
Sine and cosine, CORDIC 101
Sine, special polynomial approximation 39
Sine, table-driven 58
Sine, Tang 58
sips 125
Specker 98
SRT division 86
Subnormal numbers 12 176
SVD 101
Swartzlander 3 175
Symmetry 2 163
Table maker's dilemma 163 166
Table maker's dilemma, deterministic approach 171
Table maker's dilemma, probabilistic approach 168
Table-based methods 51
Table-driven algorithms 53 55 57 58
Takagi 81 112 114
Tang table-driven algorithms 53
Taylor expansions 29 181
Timmermann 125
Trivedi 119
Tuszinsky 107
Udo 109
ULP (unit in the last place) 13 37 65
Voider 98 101
Voider, CORDIC iteration 101
Waite 1 147
Waldschmidt 172
Walther 101
Walther, CORDIC iteration 105
Weierstrass theorem 24
Weight function 21—23 39—41
Wong and Goto's algorithm 62
Zinaty 35
Ziv 167
Zuras 173
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте