Для произвольного собственного многообразия полугрупп
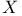
существует многообразие полугрупп

такое, что выполняются следующие три условия: 1)

покрывает многообразие
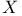
, 2) если многообразие
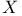
– конечно базируемое, то многообразие

– тоже конечно базируемое, 3) эквациональная теория многообразия
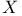
разрешима тогда и только тогда, когда разрешима эквациональная теория многообразия

.
Пусть
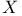
– произвольное многообразие полугрупп, заданное тождествами, зависящими от конечного числа переменных, все периодические группы которого локально конечны. Тогда выполняется одно из следующих двух условий: 1) все ниль- полугруппы из многообразия
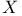
локально конечны, 2) многообразие
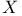
включает подмногообразие

с неразрешимой эквациональной теорией, имеющее бесконечное множество покрывающих многообразий с неразрешимой эквациональной теорией.
 |
|
О проекте
|
|
О проекте


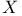 существует многообразие полугрупп
существует многообразие полугрупп  такое, что выполняются следующие три условия: 1)
такое, что выполняются следующие три условия: 1) 