|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Arrowsmith D.K., Place C.M. — Dynamical systems. Differential equations, maps and chaotic behaviour |
|
|
 |
| Предметный указатель |
Action-angle variables 149
Afline system 55 175
Algebraic type 52
Animal conflict model 218
Area-preserving map, Henon 263
Area-preserving map, Poincare 155 259
Area-preserving map, twist 261
Asymptotic stability 84 89 229
Attracting set 103 140 141
Attractor 9 141
Aubry — Mather theorem 261
Autonomous equations 6 12
Basin of attraction 91
Beats 175
Bifurcation 212
Bifurcation point 224
Bifurcation, cusp 237
Bifurcation, flip 242 245 258
Bifurcation, fold 240 242
Bifurcation, Hopf 225 228
Bifurcation, period-doubling 246 259
Bifurcation, pitchfork 293
Bifurcation, saddle-node, flows 224 226
Bifurcation, saddle-node, maps 258
Bifurcation, saddle-node, symmetric 291
Braided structure 258
Canonical local family, flip 245 293
Canonical local family, fold 242 293
Canonical system 42
Cantor set 276 280
Cantor set, fractal dimension 281
Cantor set, horseshoe map 277 278
Cantor set, iterated function scheme 281
Cantor set, tent map 276
Cellular automata 284
Centre 46
Chaotic (strange) attractor, Duffing oscillator 271
Chaotic (strange) attractor, folded band (Rossler) 251 257
Chaotic (strange) attractor, Henon 295
Chaotic (strange) attractor, iterated function scheme 282
Chaotic orbit, area preserving map 263
Chaotic orbit, homoclinic tangles 264
Chaotic orbit, horseshoe map 278
Chaotic orbit, logistic map 250
Chaotic region 266
Characteristic surface 216
Characteristic, cubic 189
Characteristic, folded 194
Characteristic, neon 194
Characteristic, resistor 189
Characteristic, triode 201
Chemical oscillator 231
Closed orbit 46 102 129
Closed orbit, hyperbolic 132
Collage 284
Competing species 180
Competitive exclusion 182
Complementary function 56
Conservative system 97
Coupled pendula 172
Critical damping 165
Cusp bifurcation 237
Decoupled system 17 58
Derivative along a curve 88
Derivative, directional 96
Diffeomorphism 132
Differentiable manifold 128
Dissipative map 268
Domain of stability 91
Doubling map 300
Duffing oscillator, twin well 254
Dynamical equations 162 223
Dynamical equations, attracting/repelling 104
Dynamical equations, capacitor 169
Dynamical equations, elliptic 253 260 261 266
Dynamical equations, hyperbolic 132
Dynamical equations, inductor 168
Dynamical equations, mutual-inductance 201
Dynamical equations, Newton’s law of cooling 11
Dynamical equations, Newton’s second law of motion 163
Dynamical equations, Poincare map/diffeomorphism 104 131
Dynamical equations, stable/unstable manifold 132
Economic model 170
Eigenspace, centre 156
Eigenspace, stable/unstable 121
Electrical circuit theory 167
Elliptic fixed point 253 260 261 266
Evolution operator 23 52
Exact differential equation 27 28
Exponential matrix 52
Family of differential equations 212 223
Feigenbaum number 246 250 280
First integral 96 147
Fixed point, phase portrait/flow 9 14
Fixed point, phase portrait/flow, hyperbolic 80 120 122
Fixed point, phase portrait/flow, isolated 11 14 16
Fixed point, phase portrait/flow, neutrally stable 86
Fixed point, phase portrait/flow, non-hyperbolic 125
Fixed point, phase portrait/flow, non-simple 46 81
Fixed point, phase portrait/flow, simple 43 77
Fixed point, phase portrait/flow, stable 84 89
Fixed point, phase portrait/flow, stable/unstable manifold 123 298
Fixed point, phase portrait/flow, unstable 87 92
Flip bifurcation 242 245 258
Flow 23
Flow box theorem 94
Focus, linear 46
Focus, non-linear 80
Fold bifurcation 240 242
Folded band (Rossler), attractor 251 257
Forcing terms 176
Fractal basin boundary 270
Fractal dimension 280
Fractal dimension, Cantor set 281
Fractal dimension, Sierpinski carpet 301
Fractal dimension, Sierpinski gasket 283 301
Generic property 226
Global phase portrait 71 237
Green’s Theorem 109
Hamiltonian 98 148
Hamiltonian flow 154
Hamiltonian system 148
Hamiltonian, generalized coordinates/momenta 148
Hamiltonian, integrable 149
Hamiltonian, normal form 149
Hamilton’s equations 98 148
Harmonic oscillator, forced 176
Harmonic oscillator, free 165
Harmonic oscillator, overdamped 166
Harmonic oscillator, second order form 163 170 171
Harmonic oscillator, underdamped 165
Heartbeat model 212
Henon, attractor 295
Henon, map, area-preserving 263 297 298
Henon, map, quadratic 258 294 296
Heteroclinic tangle 265
Holling — Tanner model 185
Homoclinic point 264
Homoclinic tangle, periodic orbit 265
Homoclinic tangle, saddle point 264
Homogeneous differential, equation 28
Hopf bifurcation 225 228 239
Hopf bifurcation, theorem 229
Improper node, linear 45
Improper node, non-linear 80
Integrating factor 27
Invariant circle 142 260 261
Invariant set 107
Invariant torus 152
Island chain 261
| Isocline 5 20
Iterated function scheme 281
Iteration 104
Jordan form, 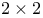 38 38
Jordan form, 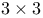 57 57
Jordan form, 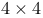 61 61
Jordan form, 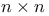 62 62
Jump assumption 193
Kirchhoff Laws 168
Kolmogorov — Arnold — Moser (KAM) theorem 261
Kolmogorov — Arnold — Moser (KAM) theorem, KAM-circle 261
Left shift 272
Level curve 88 96
Level surface 220
Liapunov, function 88
Liapunov, stability theorem 89
Liapunov, strong 90
Liapunov, weak 90
Lienard equation 191
Lienard plane 191
Limit cycle 103
Limit cycle in modelling 185
Limit cycle, criterion for non-existence 109
Limit cycle, semi-stable 104
Limit cycle, stable 104
Limit cycle, unstable 104
Limit point 101
Limit set 101
Linear change of variable 35
Linear diffeomorphism, classification 134
Linear diffeomorphism, hyperbolic 133
Linear diffeomorphism, orientation-preserving 134
Linear diffeomorphism, orientation-reversing 134
Linear mapping 35 48
Linear part 74
Linear system 11 35
Linear system, algebraic type 52
Linear system, classification of 52
Linear system, coefficient matrix of 35
Linear system, homogeneous 55
Linear system, non-homogeneous 55
Linear system, non-simple 46
Linear system, qualitative (topological) type 52
Linear system, simple 43
Linearization theorem, differential equations 77 123
Linearization theorem, Poincare maps/diffeomorphism 133 135
Linearization, Poincare map/diffeomorphism 132
Linearization, vector field 74
Linearized system 74
Liouville’s theorem 154
Local bifurcation 225
Local coordinates 75
Local family 242
Local phase portrait 71
Logistic law 12
Logistic map 245
Logistic map, chaotic orbits 250
Logistic map, eventually periodic orbits 294
Maximal solution 1
Momentum 163
Momentum, generalized 148
Natural frequency 165
Negative definite 88
Negative semi-definite 88
Neighbourhood 71
Node, linear 43
Node, non-linear 80
Non-autonomous equation 32 34
Normal coordinates 174
Normal modes 174
Ohm’s Law 168
Orbit in phase portrait 13
Orbit in terms of flow 26
Orbit of Poincare map/diffeomorphism 131
Ordinary point 93
Parametrically forced, pendulum 251 254
Partially decoupled system 18
Particular integral 56
Partitioned matrices 40 57 61 62
Partitioned matrices, application of 173
Period-doubling bifurcation, one-dimension 246
Period-doubling bifurcation, two-dimensions 257 259 296
Periodic orbit 136
Periodic orbit, Poincare — Birkhoff 261
Periodic orbit, stable/unstable manifold 137
Periodic point, phase portrait/flow 46 127
Phase line 11
Phase plane 13
Phase point 11 15 27
Phase portrait, construction of 17
Phase portrait, one-dimension 8
Phase portrait, qualitative type of 52
Phase portrait, restriction of 71
Phase portrait, two-dimensions 13
Piecewise modelling 195
Pitchfork bifurcation 293
Plant-pollinator model 226
Poincare (first return) map 104 129
Poincare (first return) map for Hamiltonian flow 153 155
Poincare (first return) map, area-preserving 155 259
Poincare map/diffeomorphism 136
Poincare — Bendixson theorem 106
Poincare — Birkhoff theorem 261
Polar coordinates 17
Positive definite 88
Positive semi-definite 88
Positively invariant set 107
Prey-predator problem 183 185
Principal directions 48 81
q-cycle 136
Qualitative behaviour 4 8 14 16 120 125 128 132
Qualitative equivalence 4 9 10 16 51
Qualitative equivalence of families of differential equations 239
Quasi-periodic motion 128 138
Rationally independent numbers 127
Rayleigh equation 209 292
Regularization 193
Relaxation oscillations 190
Renormalization 280 300 301
Repellor 9
Resonance 177
resonant frequency 179
Robust system 185
Rossler attractor 251 257
Rotation interval 261 297
Rotation number 261 297
Saddle connection 95 99 105 107
Saddle connection, bifurcation 239
Saddle connection, heteroclinic 265
Saddle connection, homoclinic 264
Saddle point, linear 44 121
Saddle point, non-linear 80 123
Saddle point, spiral 122 156
Saddle-node bifurcation, flows 224
Saddle-node bifurcation, maps 258
Saddle-node bifurcation, symmetric 291
Sawtooth oscillations 197
Sensitive dependence on, initial conditions 274
Separable differential equation 27
Separalrix 44 80
Separation of variables 6 27
Shunt 9
Sierpinski carpet 301
Sierpinski gasket 283 285
Similar matrices 36
Similarity classes 37
Similarity types 38
simple pendulum 208
Simply connected region 109
Smale horseshoe map 276
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте