Àâòîðèçàöèÿ
Ïîèñê ïî óêàçàòåëÿì
Erdelyi A. — Higher Transcendental Functions, Vol. 2
Îáñóäèòå êíèãó íà íàó÷íîì ôîðóìå Íàøëè îïå÷àòêó?
Íàçâàíèå: Higher Transcendental Functions, Vol. 2Àâòîð: Erdelyi A. Àííîòàöèÿ: The Bulletin of the London Mathematical Society hailed this three-volume series as "The most widely cited mathematical works of all time and a basic reference source for generations of applied mathematicians and physicists throughout the world." Working from extensive notes on familiar special functions by the renowned mathematician Harry Bateman, a team of editors not only finished Bateman's original project but also made significant advances in mathematical analysis. The books, which can be used independently of each other, consist of Volume 1, which focuses on hypergeometric series; Volume 2, an exploration of Bessel functions, orthogonal polynomials, and elliptic functions and integrals; and Volume 3, an examination of automorphic functions, spheroidal and ellipsoidal wave functions, and other functions.
ßçûê: Ðóáðèêà: Ìàòåìàòèêà /Ñòàòóñ ïðåäìåòíîãî óêàçàòåëÿ: Ãîòîâ óêàçàòåëü ñ íîìåðàìè ñòðàíèö ed2k: ed2k stats Ãîä èçäàíèÿ: 1955Êîëè÷åñòâî ñòðàíèö: 408Äîáàâëåíà â êàòàëîã: 13.07.2005Îïåðàöèè: Ïîëîæèòü íà ïîëêó |
Ñêîïèðîâàòü ññûëêó äëÿ ôîðóìà | Ñêîïèðîâàòü ID
Ïðåäìåòíûé óêàçàòåëü
232 273 10 153 264 232 29 $B_{n;\mu,\nu}(z) Gegenbauer’s polynomial 34 174 117 143 330 143 271 134 136 35 271 299 305 285 147 4 285 8 193 37 149 $I_{\nu}(z) modified Bessel function of the first kind 5 375 21 35 4 300 306 6 134 5 188 140 38 195 32 168 345 171 170 180 181 34 34 40 40 183 277 183 42 274 ff. 42 12 250 4 2 48 34 147 332 2 115 234 317 329 330 vol. I p. 323 328 133 133 140 133 15 374 321 321 321 314 317 300 313 314 317 289 290 270 4 328 34 330 317 301 313 329 330 328 355 360 329 A(t) Airy function 200 Abelian integrals 295 ff. Absolute invariant 375 Airy’s integrals 22 am u Jacobi’s function 322 Anger’s function 35 ff. 84 99 103 Appell series 280 ff. Approximation of quadratically integrable functions 156 Associated polynomials 162 ff. Automorphic functions 296 374 Barnes’ integral representations of Bessel functions 21 ff. Basset’s function see “Modified Bessel function of the third kind” bei 6 ber x, 6 Bessel coefficients 6 Bessel coefficients, generating function for 7 Bessel coefficients, integral representations for 13 ff. 81 Bessel function of the first kind 4 Bessel function of the first kind, derivative with respect to the order 7 Bessel function of the first kind, duplication formula for 45 Bessel function of the first kind, inequalities for 14 66 Bessel function of the first kind, series involving 63 ff. Bessel function of the first kind, series involving, Bessel function of the first kind, zeros of 59 ff. Bessel function of the second kind 4 Bessel function of the second kind, of integer order 7 Bessel function of the second kind, of order zero 8 Bessel function of the second kind, zeros of 61 ff. Bessel function of the third kind 4 Bessel function of the third kind, zeros of 62 Bessel functions, addition theorems for 43 ff. 101 Bessel functions, addition theorems for, Bessel functions, analytic continuation of 12 80 Bessel functions, and wave motion 2 ff. Bessel functions, as limits of Jacobi polynomials 173 Bessel functions, as limits of Laguerre polynomials 191 Bessel functions, asymptotic expansions for 22 ff. 85 Bessel functions, asymptotic expansions for, differential equations for 13 Bessel functions, differentiation formulas for 11 Bessel functions, integral representations for 14 ff. 57 81 Bessel functions, integrals involving 45 ff. 57 90 Bessel functions, notations for 3 Bessel functions, of imaginary order 87 ff. Bessel functions, of order see “Spherical Bessel functions” Bessel functions, of order 10 79 Bessel functions, power series for products of 10 ff. Bessel functions, recurrence relations for 12 Bessel functions, relations with Legendre functions 55 ff. Bessel functions, series involving 58 63 98 Bessel functions, series involving, Bessel functions, Wronskians of 12 79 Bessel functions, series involving, Bessel functions, zeros of 58 ff. Bessel polynomials 10 Bessel’s differential equation 3 ff. Bessel’s differential equation, Bessel’s inequality 157 Bilinear forms 284 Biorthogonal system 265 Birational invariant 295 Birational transformation 295 C (x) Fresnel integral 149 C (x, 149 cd u Glaisher’s function 322 cell 325 Chi x modified cosine integral 146 Christoffel numbers 161 Christoffel — Darboux formula 159 269 Ci x cosine integral 145 Classical orthogonal polynomials 163 ff. (see also “Legendre Gegenbauer Hermite Laguerre Classical orthogonal polynomials, characterization of 164 Classical orthogonal polynomials, differential equation for 166 ff. Classical orthogonal polynomials, differential equation for, properties of 164 166 Classical orthogonal polynomials, differentiation formula for 167 cn u Jacobi’s elliptic function 322 Complete elliptic integrals see “Elliptic integrals“ Confluent hypergeometric functions, expansion in terms of parabolic cylinder functions 124 Conformal mappings, involving elliptic functions and integrals 376 ff. Convergence in mean of generalized Fourier expansions 157 Convolution 45 Cornu’s spiral 151 Cosine integral 145 ff. cs u Glaisher’s function 322 Cut Bessel functions 22 dc u Glaisher’s function 322 Didon series 280 ff. Didon series, Dini series of Bessel functions 70 ff. dn u Jacobi’s elliptic function 322 Doubly-periodic functions 323 ff. (see also “Elliptic functions“) ds u Giaisher’s function 322 E(u) Jacobi’s function 343 Ei (x) exponential integral 143 Elliptic functions 294 ff. 322 325 Elliptic functions, addition theorems satisfied by 328 Elliptic functions, differential equations satisfied by 327 Elliptic functions, expression of, in terms of 335 Elliptic functions, expression of, in terms of sigma functions 337 Elliptic functions, expression of, in terms of zeta functions 336 ff. Elliptic functions, general properties of 325 ff. Elliptic functions, integrals of, expressed in terms of Weierstrass’ functions 337 Elliptic functions, Jacobian 322 ff. 340 Elliptic functions, Jacobian, addition theorems for 344 Elliptic functions, Jacobian, degenerate cases of 354 Elliptic functions, Jacobian, expressed in terms of theta functions 362 Elliptic functions, Jacobian, expressed in terms of Weierstrass’ functions 340 ff. Elliptic functions, Jacobian, Landen’s transformation of 372 Elliptic functions, Jacobian, linear transformation of 367 ff. Elliptic functions, Jacobian, periods, zeros, poles and residues of 341 Elliptic functions, Jacobian, quadratic transformations of 372 ff. Elliptic functions, Jacobian, special values of 346 ff. Elliptic functions, Jacobian, with 349 ff. Elliptic functions, Neville’s notation for 294 342 Elliptic functions, order of 326 Elliptic functions, residues of 326 Elliptic functions, transformations of 365 ff. Elliptic functions, Weierstrass 323 328 Elliptic functions, Weierstrass’ duplication formula for 333 Elliptic functions, Weierstrass’ expressed in terms of theta functions 360 ff. Elliptic functions, Weierstrass’, addition theorem for 332 ff. Elliptic functions, Weierstrass’, degenerate cases of 339 ff. Elliptic functions, Weierstrass’, differential equation for 331 ff. Elliptic functions, Weierstrass’, Landen’s transformation of 371 ff. Elliptic functions, Weierstrass’, linear transformations of 367 ff. Elliptic functions, Weierstrass’, quadratic transformations of 371 ff. Elliptic functions, Weierstrass’, with real invariants 338 ff. Elliptic integrals 294 ff. Elliptic integrals, addition theorems for 315 Elliptic integrals, complete, expressed in terms of hypergeometric series 318 Elliptic integrals, complete, integration formulas for 322 Elliptic integrals, complete, Legendre’s relation for 320 Elliptic integrals, complete, of the first, second, and third kind 314 317 Elliptic integrals, complete, particular cases of 320 Elliptic integrals, complete, transformations of 318 ff. Elliptic integrals, differentiation formulas for 317 321 Elliptic integrals, expressed in terms of theta functions 363ff. Elliptic integrals, expressed in terms of Weierstrass’ functions 337 ff. Elliptic integrals, interchange theorem for 303 ff. 315 Elliptic integrals, inversion of 322 ff. Elliptic integrals, Landen’s transformation of 317 Elliptic integrals, Legendre’s form of 300 ff. 314 Elliptic integrals, Legendre’s, evaluation of 308 ff. Elliptic integrals, linear transformations of 315 ff. Elliptic integrals, Low’s form of 301 Elliptic integrals, moduli of periodicity of 303 Elliptic integrals, of the first, second, and third Elliptic integrals, kinds 299 ff. 313 Elliptic integrals, periods of 303 314 Elliptic integrals, reduction of 296 ff. 304 Elliptic integrals, reduction to Legendre’s normal form 305 ff. Elliptic integrals, reduction to Weierstrass’ normal form 304 ff. Elliptic integrals, singularities of 303 314 Elliptic integrals, Weierstrass’ form of 299 ff. Elliptic modular functions 374 ff. Equianharmonic elliptic functions and integrals 306 320 Erf x error function 147 Erfc x complementary error function 147 Erfi x modified error function 147 Error functions 147 ff. Error functions, connection with parabolic Error functions, cylinder functions 119 Error functions, expansions in terms of Bessel Error functions, functions 148 Error functions, power series expansions of 147 Error functions, repeated integrals of 149 Exponential integrals 143 ff. Exponential integrals, expressed in terms of confluent Exponential integrals, hypergeometric functions 143 Exponential integrals, expressed in terms of incomplete Exponential integrals, gamma functions 143 Exponential integrals, generalizations of 145 F Incomplete elliptic integral of the first kind 300 313 Field of elliptic functions 327 Field, differential 327 Fourier coefficients (generalized) 156 Fourier series (generalized) 156 Fourier — Bessel series 70 ff. 104 Fresnel integrals 149 ff. Fresnel integrals, connection with error functions 149 Fresnel integrals, connection with incomplete gamma functions 149 Functions of the parabolic cylinder see “Parabolic cylinder functions“ Functions of the paraboloid of revolution 126 ff. Fundamental period-parallelogram, 325 Fundamental region of the 375 Fundamental region of the modular group 375 Funk — Hecke theorem 247 Gauss transforms 194 Gauss transforms, multi-dimensional 289 ff. Gegenbauer polynomials 164 174 235 Gegenbauer polynomials, asymptotic behavior as n 198 Gegenbauer polynomials, connection with Legendre functions 177 Gegenbauer polynomials, expressed as hypergeometric functions 175 ff. Gegenbauer polynomials, generating functions of 177 Gegenbauer polynomials, inequalities for 206 ff. Gegenbauer polynomials, integral representations for 177 Gegenbauer polynomials, monotonic properties of 208 Gegenbauer polynomials, recurrence formula for 175 Gegenbauer polynomials, Rodrigues’ formula for 175 Gegenbauer polynomials, series of 177 ff. 213 Gegenbauer polynomials, zeros of 203 ff. 387 Gegenbauer’s addition theorem for Bessel functions 43 ff. Gegenbauer’s polynomials 34 Generalized Dirichlet series 72 ff. Genus of algebraic curves 295 Glaisher’s notation,of Jacobian elliptic functions 322 Graf’s addition theorem for Bessel functions 44 ff. Gram’s determinant 155 Gubler’s integral representations, of Bessel functions 17 ff. Hankel’s function see “Bessel function of the third kind“ Hankel’s infinite integral, involving Bessel functions 49 Hankel’s integral representations of Bessel functions 15 ff. Hankel’s inversion theorem 73 Hardy’s generalization of 73 ff. Hardy’s generalization of, Hankel’s symbol ( 10 Harmonic polynomials 237 ff. Harmonic polynomials, complete set of 239 ff. Hermite polynomials 164 192
Ðåêëàìà
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



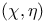 scalar product of vectors
scalar product of vectors  Hankel’s symbol
Hankel’s symbol 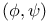 scalar product of functions
scalar product of functions 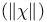 length of vector
length of vector 
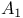 (t),
(t), 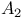 (t) Airy integrals
(t) Airy integrals  Gegenbauer polynomials
Gegenbauer polynomials 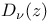 Parabolic cylinder function
Parabolic cylinder function 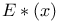 modified exponential integral
modified exponential integral 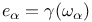
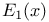 , exponential integral
, exponential integral 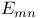 Appell’s polynomials
Appell’s polynomials 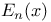 function used in astrophysics and nuclear physics
function used in astrophysics and nuclear physics 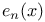 Truncated exponential series
Truncated exponential series 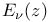 Weber’s function
Weber’s function 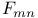 Appell’s polynomial
Appell’s polynomial 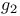 ,
, 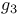 invariants of Weierstrass’ elliptic functions
invariants of Weierstrass’ elliptic functions 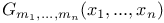 Hermite polynomials of several variables
Hermite polynomials of several variables 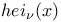 ,
, 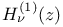 ,
, 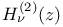 Bessel functions of the third kind
Bessel functions of the third kind 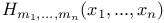 Hermite polynomial of several variables
Hermite polynomial of several variables 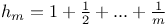
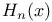 Hermite polynomials
Hermite polynomials 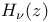 Struve’s function
Struve’s function 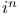 erfc x repeated integral of error function
erfc x repeated integral of error function 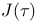 absolute invariant
absolute invariant 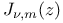 cut Bessel function of the first kind
cut Bessel function of the first kind 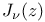 Anger’s function
Anger’s function  modulus of Jacobi’s elliptic functions and integrals
modulus of Jacobi’s elliptic functions and integrals  ,
, 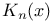 function used in astrophysics and nuclear physics
function used in astrophysics and nuclear physics 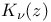 modified Bessel function of the third kind
modified Bessel function of the third kind 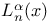 Laguerre polynomial
Laguerre polynomial 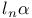 polynomial
polynomial 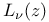 modified Struve function
modified Struve function 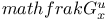 Gauss transform
Gauss transform 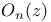 Neumann’s polynomial
Neumann’s polynomial 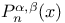 Jacobi polynomial
Jacobi polynomial 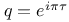
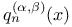 polynomials associated with Jacobi polynomials
polynomials associated with Jacobi polynomials 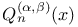 Jacobi function of the second kind
Jacobi function of the second kind 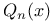 Legendre function of the second kind
Legendre function of the second kind 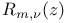 Lommel’s polynomials
Lommel’s polynomials 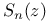 Schl
Schl fli’s polynomial
fli’s polynomial 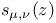 Lommel’s function
Lommel’s function 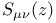 Lommel’s function
Lommel’s function 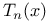 Tchebichef polynomial
Tchebichef polynomial 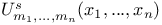 polynomials of Hermite and Didon
polynomials of Hermite and Didon 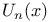 Tchebichef polynomial
Tchebichef polynomial 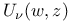 Lommel’s function of two variables
Lommel’s function of two variables 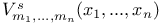 polynomials of Hermite and Didon
polynomials of Hermite and Didon 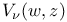 Lommel’s function of two variables
Lommel’s function of two variables 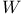 Wronskian
Wronskian 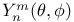 spherical surface harmonic
spherical surface harmonic 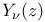 Bessel function of the second kind
Bessel function of the second kind 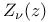 Bessel function
Bessel function 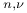 (z) Gegenbauer’s polynomial
(z) Gegenbauer’s polynomial 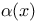 error function
error function 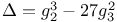 discriminant
discriminant  Laplace’s operator
Laplace’s operator 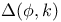
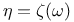 ,
, 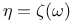
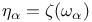
 Euler — Mascheroni constant
Euler — Mascheroni constant 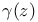 Weierstrass’ elliptic function
Weierstrass’ elliptic function 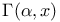 complementary incomplete gamma function
complementary incomplete gamma function 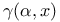 incomplete gamma function
incomplete gamma function 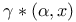 modified incomplete gamma function
modified incomplete gamma function 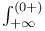 loop integral
loop integral 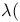 \tau)$ modular function
\tau)$ modular function 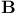 complete elliptic integral
complete elliptic integral 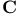 complete elliptic integral
complete elliptic integral 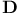 complete elliptic integral
complete elliptic integral 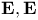 complete elliptic integrals of the second kind
complete elliptic integrals of the second kind 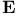 Incomplete elliptic integral of the second kind
Incomplete elliptic integral of the second kind 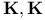 complete elliptic integrals of the first kind
complete elliptic integrals of the first kind 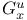 multi-dimensional Gauss transform
multi-dimensional Gauss transform 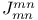 Appell’s polynomial
Appell’s polynomial 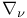 Bessel’s differential operator
Bessel’s differential operator 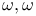 periods of Weierstrass’ elliptic functions
periods of Weierstrass’ elliptic functions 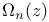 Neumann’s polynomial
Neumann’s polynomial 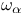 periods of Weierstrass’ elliptic functions
periods of Weierstrass’ elliptic functions  complete elliptic integral of the third kind
complete elliptic integral of the third kind 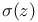 Weierstrass’ sigma function
Weierstrass’ sigma function  sigma functions
sigma functions 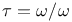
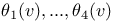 Theta functions
Theta functions 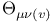 Hermite’s theta function
Hermite’s theta function 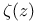 Weierstrass’ zeta function
Weierstrass’ zeta function 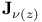
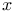 ,
,  Kelvin’s functions
Kelvin’s functions 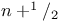
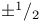
 ) generalized Fresnel integral
) generalized Fresnel integral 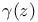
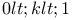
 -group
-group 

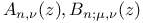
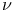 , m)
, m)