В 1954 г. Л. Ниренберг получил следующий хорошо известный результат: если
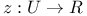
,
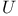
– область в
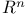
, является решением класса
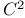
эллиптического уравнения с частными производными

2-го порядка, где
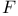
– функция класса
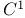
, то тогда частные производные

2-го порядка функции
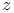
локально непрерывны по Гельдеру в
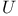
. Одновременно с Ниренбергом Ч. Морри получил аналогичный результат для эллиптических систем нелинейных уравнений 2-го порядка. В настоящей статье получен такой же результат, но уже для эллиптических решений систем нелинейных дифференциальных уравнений с частными производными произвольного порядка и весьма общего вида. В основе его доказательства лежат результаты исследований последних лет автора статьи, посвященных изучению явлений устойчивости в

– норме классов отображений.
 |
|
О проекте
|
|
О проекте


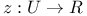 ,
, 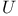 – область в
– область в 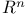 , является решением класса
, является решением класса 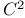 эллиптического уравнения с частными производными
эллиптического уравнения с частными производными

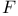 – функция класса
– функция класса 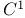 , то тогда частные производные
, то тогда частные производные  2-го порядка функции
2-го порядка функции 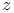 локально непрерывны по Гельдеру в
локально непрерывны по Гельдеру в  – норме классов отображений.
– норме классов отображений.