|
Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета |
| Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск |
|
|
© Электронная библиотека попечительского совета мехмата МГУ, 2004-2026 |
|
О проекте |
|
О проекте
|


 изучается разрешимость некоторых аналогов первой начально-краевой задачи для уравнений
изучается разрешимость некоторых аналогов первой начально-краевой задачи для уравнений  . Функция
. Функция  здесь моделирует функцию
здесь моделирует функцию  , для функции
, для функции 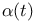 , определяющей область
, определяющей область 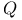 , выполняется условие
, выполняется условие  при
при ![$t\in[0, T]$](/math_tex/06148171bb6ea578759a16f3691d5f6f82.gif) и одно из условий
и одно из условий  . Наряду с доказательством теорем существования регулярных решений изучаемых краевых задач, в работе приводятся некоторые результаты о поведении энергетической нормы решения при
. Наряду с доказательством теорем существования регулярных решений изучаемых краевых задач, в работе приводятся некоторые результаты о поведении энергетической нормы решения при 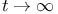 .
.