В работе получен следующий результат.
Теорема 1. Пусть
![$f:[\alpha,beta]\to\Bbb R^m$](/math_tex/d195dd57f06abbbf6125d9b47e17a39c82.gif)
– функция, непрерывная на отрезке
![$[\alpha,\beta]\subset \Bbb R$](/math_tex/7a5f6206dec861f6638ce1286480a79c82.gif)
и дифференцируемая на интервале
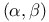
, где
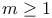
и
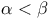
. Тогда отношение
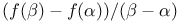
есть выпуклая комбинация
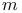
значений производной
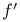
, т. е. существуют числа
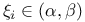
и
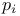
,
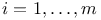
, такие, что
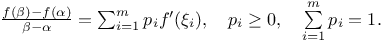
}\par Для вещественнозначных функций (при
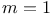
) теорема 1 совпадает с классической теоремой Лагранжа. Для случая дифференцируемых отображений

, производная
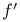
которых непрерывна слева на
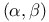
или непрерывна справа на
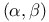
, утверждение теоремы 1 было получено в работе McLeod R. M. “Mean value theorems for vector valued functions // Proc. Edinburgh Math. Soc. (Ser. 2). 1965. V. 14. P. 197–209.”
 |
|
О проекте
|
|
О проекте


![$f:[\alpha,beta]\to\Bbb R^m$](/math_tex/d195dd57f06abbbf6125d9b47e17a39c82.gif) – функция, непрерывная на отрезке
– функция, непрерывная на отрезке ![$[\alpha,\beta]\subset \Bbb R$](/math_tex/7a5f6206dec861f6638ce1286480a79c82.gif) и дифференцируемая на интервале
и дифференцируемая на интервале 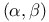 , где
, где 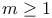 и
и 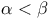 . Тогда отношение
. Тогда отношение 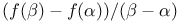 есть выпуклая комбинация
есть выпуклая комбинация 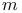 значений производной
значений производной 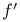 , т. е. существуют числа
, т. е. существуют числа 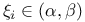 и
и 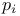 ,
, 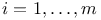 , такие, что
, такие, что
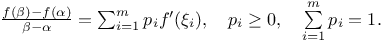
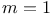 ) теорема 1 совпадает с классической теоремой Лагранжа. Для случая дифференцируемых отображений
) теорема 1 совпадает с классической теоремой Лагранжа. Для случая дифференцируемых отображений  , производная
, производная 