Главная    Ex Libris    Книги    Журналы    Статьи    Серии    Каталог    Wanted    Загрузка    ХудЛит    Справка    Поиск по индексам    Поиск    Форум   
blank
Авторизация

       
blank
Поиск по указателям

blank
blank
blank
Красота
blank
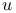Половинкин В.И. — Формула для функций, реализующих функционалы
Половинкин В.И. — Формула для функций, реализующих функционалы



Обсудите книгу на научном форуме



Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Формула для функций, реализующих функционалы

Автор: Половинкин В.И.

Аннотация:

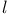Выводится формула для функций $u$, реализующих функционалы $l$, принадлежащие пространству, сопряженному к $L_p^m(E_n)$, $p\in(1,\infty)$, в виде
$ (l,f)=\int\limits_{E_n}\sum\limits_{|\alpha|=m} \frac{m!}{\alpha!}u^{(\alpha)}(x)f^{(\alpha)}(x) dx. $
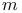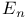Здесь $f$ – представитель $F\in L_p^m(E_n)$; $u$ считается обладающей обобщенными производными порядка $m$, суммируемыми по $n$-мерному пространству $E_n$ в степени $p(p-1)^{-1}$; носитель $l$ не предполагается ограниченным.


Язык: ru

Рубрика: Математика/

Тип: Статья

Статус предметного указателя: Неизвестно

ed2k: ed2k stats

Год издания: 1999

Количество страниц: 6

Добавлена в каталог: 12.09.2009

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID
blank
Предметный указатель
blank
Реклама
blank
blank
HR
@Mail.ru
       © Электронная библиотека попечительского совета мехмата МГУ, 2004-2024
Электронная библиотека мехмата МГУ | Valid HTML 4.01! | Valid CSS! О проекте