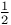Пусть Ф – ссоциативное коммутативное кольцо с единицей, содержащее . Рассматривается гомотоп алгебры Новикова, т.е. алгебра 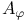, полученная из алгебры Новикова 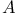посредством производной операции 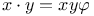на Ф-модуле , где отображение удовлетворяет равенству 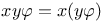, и находятся условия, при которых гомотоп алгебры Новикова снова является алгеброй Новикова.