Рассматриваются линейные топологические пространства:
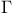
, состоящее из функций, аналитических в выпуклой области

и ограниченных с системой весов

,

– выпуклые функции
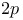
вещественных переменных, и
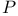
, состоящее из целых функций

переменных, ограниченных с системой весов

, где

, рассматриваемая как функция
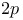
вещественных переменных, является преобразованием Лежандра функции

. При одном условии “правильности” роста функций

доказывается теорема О. В. Епифанова: {\sl сильно сопряженное к
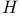
пространство
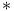
-топологически изоморфно пространству
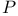
, изоморфизм устанавливается с помощью преобразования Лапласа}.
 |
|
О проекте
|
|
О проекте


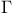 , состоящее из функций, аналитических в выпуклой области
, состоящее из функций, аналитических в выпуклой области  и ограниченных с системой весов
и ограниченных с системой весов  ,
,  – выпуклые функции
– выпуклые функции 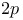 вещественных переменных, и
вещественных переменных, и 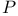 , состоящее из целых функций
, состоящее из целых функций  переменных, ограниченных с системой весов
переменных, ограниченных с системой весов  , где
, где  , рассматриваемая как функция
, рассматриваемая как функция  доказывается теорема О. В. Епифанова: {\sl сильно сопряженное к
доказывается теорема О. В. Епифанова: {\sl сильно сопряженное к 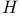 пространство
пространство 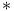 -топологически изоморфно пространству
-топологически изоморфно пространству 