We define a centrally symmetric analogue of the cyclic polytope and study its facial structure. We conjecture that our polytopes provide asymptotically the largest number of faces in all dimensions among all centrally symmetric polytopes with
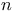
vertices of a given even dimension

when
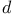
is fixed and n grows. For a fixed even dimension

and an integer

we prove that the maximum possible number of
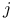
-dimensional faces of a centrally symmetric
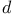
-dimensional polytope
with
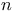
vertices is at least
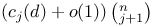
for some

and at most

as
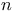
grows.We show that

and conjecture that the bound is best possible.
 |
|
О проекте
|
|
О проекте


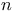 vertices of a given even dimension
vertices of a given even dimension  when
when 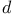 is fixed and n grows. For a fixed even dimension
is fixed and n grows. For a fixed even dimension  we prove that the maximum possible number of
we prove that the maximum possible number of 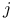 -dimensional faces of a centrally symmetric
-dimensional faces of a centrally symmetric 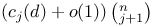 for some
for some  and at most
and at most  as
as  and conjecture that the bound is best possible.
and conjecture that the bound is best possible.