|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Волевич Л.Р., Гиндикин С.Г. — Обобщенные функции и уравнения в свертках |
|
|
 |
| Предметный указатель |
 10 10
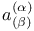 10 10
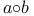 256 256
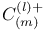 85 85
 145 145
 168 168
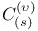 149 149
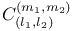 59 59
 , ,  165 165
 168 168
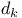 9 9
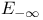 68 68
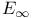 73 73
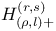 206 206
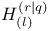 190 190
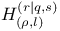 207 207
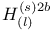 275 275
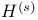 , , 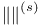 24 24
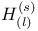 , , 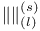 27 27
 145 154 145 154
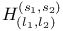 59 59
 168 168
 153 153
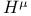 231 231
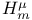 254 254
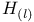 , , 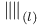 23 23
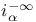 68 68
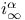 73 73
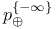 293 293
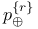 294 295 294 295
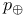 190 190
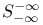 253 255 253 255
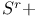 , , 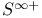 249 249
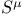 , , 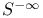 231 233 231 233
 272 272
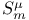 255 267 255 267
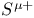 242 242
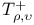 273 273
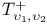 168 168
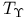 272 272
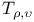 271 271
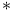 37 40 37 40
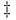 a 256 a 256
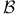 231 234 231 234
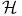 286 286
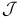 7 14 7 14
 59 59
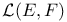 66 66
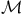 17 17
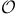 9 17 9 17
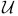 284 285 284 285
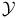 312 312
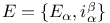 67 67
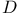 145 148 149 157 145 148 149 157
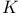 145 145
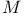 150 150
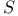 145 148 155 145 148 155
![${ _{[\omega]}}a(D){\varphi}$](/math_tex/bde5dbe480c8c635e666fd4b1d8b396482.gif) 56 56
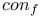 42 42
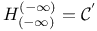 31 31
![${H^{(r, s)}_{(l)}}{[0]}$](/math_tex/997d9e64d15ac98326646c97de53d3d482.gif) 206 206
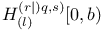 222 222
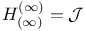 31 31
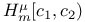 268 268
![${H^{\mu}}{[c_{1}, c_{2}]}$](/math_tex/01e5c8c615eb703be30ca50ae7fabd8d82.gif) 246 246
 152 152
![${[ ]}_{(q)}$](/math_tex/d39919ca1d711895153c2de13a37054f82.gif) 233 233
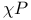 177 177
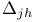 46 46
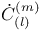 14 14
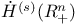 117 117
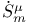 267 267
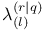 193 193
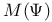 19 19
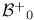 266 266
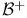 242 242
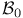 254 254
 272 272
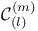 , , 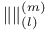 11 11
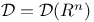 10 10
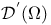 71 71
 272 272
![${\mathcal{F}}{ _{[\omega]}}{\varphi}$](/math_tex/2d56de71be87d3695e9bd32c81cf67c582.gif) 56 56
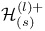 93 93
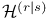 311 311
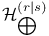 312 312
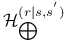 311 311
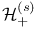 , , 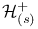 91 91
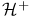 197 197
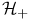 , , 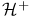 88 88
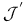 8 16 8 16
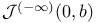 222 222
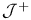 85 85
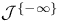 285 285
![${\mathcal{J}}^{{\{}m{\}}}_{[+]}$](/math_tex/ce0d48632f1c50ca042a25a5f33da7b382.gif) , , ![${\mathcal{J}}^{{\{}-{\infty}{\}}}_{[+1]}$](/math_tex/284a0ad8effab661a9514486b732f39e82.gif) 186 195 210 186 195 210
![${\mathcal{J}}_{[+]}$](/math_tex/4837890421af5ba9b9a45a1af5967b2682.gif) 186 186
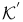 59 59
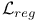 71 71
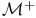 , , 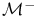 87 87
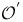 9 19 9 19
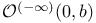 222 222
![${\mathcal{O}}^{{\{}-{\infty}{\}}}_{[+]}$](/math_tex/54a21d28255c4fc6144bdc7572c1079482.gif) 186 203 221 186 203 221
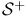 204 204
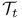 107 107
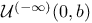 222 222
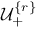 , , 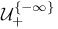 211 211
![${\mathcal{V}}^{(-{\infty})}_{[+]}$](/math_tex/c3ec73bc1d9d5118137b546849a2fadb82.gif) , , ![${\mathcal{W}}^{(-{\infty})}_{[+]}$](/math_tex/3eac6d553e16e758110bacbc45d3952582.gif) 221 221
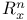 9 9
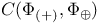 284 284
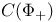 127 127
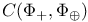 281 281
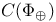 131 131
 151 151
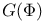 48 48
 151 151
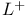 168 168
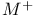 165 165
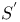 149 157 149 157
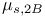 276 276
| 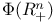 104 104
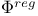 287 287
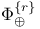 , , 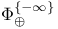 292 294 292 294
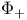 , , 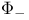 82 82
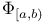 , , ![${\Phi}_{(a, b]}$](/math_tex/aae8cbcb9c4a5738c208b306f2ce2f1d82.gif) 83 83
![${\Phi}_{[\omega]}$](/math_tex/4c92a7a167312c8a015942b2d0d5414d82.gif) 54 54
![${\Phi}_{[\rho]}$](/math_tex/4cca30e7eee7c8778c12657ef5ea98d582.gif) 83 83
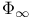 , , 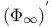 125 125
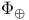 82 82
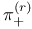 191 191
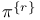 295 295
![${\Psi}^{[\omega]}$](/math_tex/33558302e511c9ddfa6f05d1e321459582.gif) 56 56
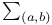 , , 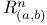 121 121
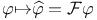 20 20
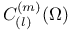 , , 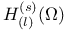 121 121
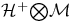 , , 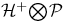 215 215
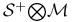 221 221
![${{\mid} {\mid}}^{(s)}_{(l)[\rho]}$](/math_tex/6585f2d7a1e8b472fbaad92ffdc0a1ff82.gif) , , ![${{\parallel} {\parallel}}^{(s)}_{(l)[\rho]}$](/math_tex/b52b64ad8895973d92b4356f8d78f50782.gif) 83 83
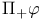 107 107
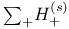 115 115
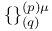 255 255
a(x;D) 21
i 20
W(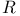 ), W(K) 291 ), W(K) 291
Борнологическое пространство 66
Бочечное пространство 80
Граничные задачи для псевдодифференциальных уравнений 224
Двойственность шкал 78
Дифференциальные операторы 2b-параболические 275
Дифференциальные операторы N-параболические 275
Индуктивная топология 69
Индуктивная шкала 68 69
Индуктивный предел 9 52
Индуктивный предел л. т. п. 68
Индуктивный предел регулярный 16 69
Индуктивный предел рефлексивных банаховых пространств 69
Индуктивный предел строгий 69
Каноническая факторизация 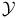 312 325 312 325
Каноническая факторизация в 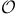 , , 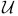 , , 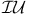 , , 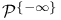 289 289
Метод Винера — Хопфа 295 296
Многоугольник Ньютона полинома 181
Мультипликаторы 19 51
Непрерывные операторы в л. т. п. 66
Непрерывные операторы из  в в  15 15
Непрерывные операторы из 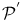 в в 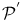 32 32
Непрерывные операторы из индуктивной шкалы в индуктивную 70 71
Непрерывные операторы из индуктивной шкалы в проективную 77 78
Непрерывные операторы из проективной шкалы в индуктивную 76
Непрерывные операторы из проективной шкалы в проективную 73 74
Операторы Винера — Хопфа 280
Операторы свертки 9 42 47 49 51
Операторы свертки в конечной полосе 135
Операторы свертки в пространствах 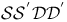 161 161
П. д. о. с условием трансмиссии 248
Параметрикс дифференциального оператора 327 329
Парсеваля неравенства 8 20
Парсеваля равенство 21
Первая аксиома счетности 66 71
Плюрисубгармоническая функция 177
Полиномы 2b-параболические 141
Полиномы N-параболические 181
Полиномы гиперболические 141
Полиномы гипоэллиптические 178
Полиномы доминантно корректные 182
Полиномы плюрипараболические 182
Полиномы строго гиперболические 141
Полиномы экспоненциально корректные 141
Поляры 66
Преобразование Фурье 20
Проективная топология 73
Проективная шкала 72
Проективный предел л. т. п. 9 72
Пространство Фреше 49
Псевдодифференциальные операторы 21
Пэли — Винера теорема 88
Распределения 9
Распределения быстро убывающие 19
Распределения медленно растущие 19
Регулярно ограниченные множества 69
Регулярно ограниченные множества в 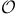 18 18
Регулярные операторы из 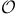 в в 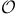 18 18
Регулярные операторы из 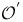 в в 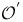 35 35
Регулярные операторы из индуктивного предела в индуктивный 71
Регулярные операторы из проективного предела в индуктивный 76
Регулярные операторы из проективного предела в проективный 74
Свертка 37
Свертка в фактор-пространстве 129
Свертка распределений 39
Сверточные уравнения 47 51
Сверточные уравнения в фактор-пространствах 135
Свертыватели 9 48 49
Свертыватели Винера — Хопфа 279 281
Свертыватели с условием трансмиссии 279 283
Символ 2b-параболический 141
Символ псевдодифференциального оператора 21
Символ строго гиперболический 141
Символ удовлетворяющий условию трансмиссии 249
Согласованное семейство отображений шкал 67
Счетно-гильбертовы пространства 8 31
Теорема вложения С.Л. Соболева 8 29
Теорема об обратном операторе С. Банаха 51
Теоремы о ядре 61 64 162
Условие корректности для уравнения волнового 140
Условие корректности для уравнения теплопроводности 140
Условие корректности для уравнения Шредингера 140
Условие Петровского 139
Условие Шапиро — Лопатинского 305
Условие экспоненциальной корректности 169
Фактор-пространства, операторы свертки 129
Фактор-пространства, сверточные уравнения 137
Фактор-пространства, шкалы 98
Фредгольмовый оператор 309
Фундаментальное решение 51
Функции быстро убывающие, бесконечно дифференцируемые 19
Функции медленно возрастающие, бесконечно дифференцируемые 19
Экспоненциально корректный дифференциальный оператор 144 164 177
[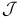 ], [ ], [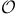 ], [ ], [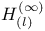 ] 293 ] 293
[ ] 293 ] 293
|x| 9
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




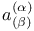
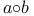
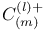


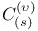
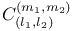
 ,
, 

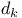
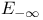
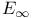
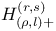
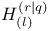
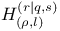
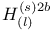
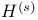 ,
, 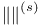
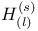 ,
, 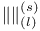

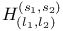


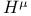
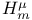
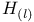 ,
, 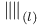
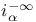
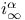
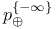
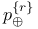
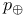
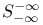
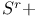 ,
, 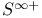
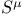 ,
, 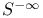

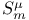
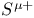
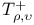
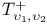
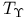
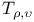
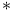
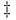 a
a 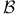
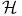
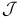

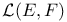
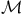
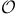
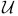
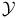
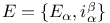
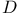
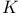
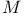
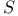
![${ _{[\omega]}}a(D){\varphi}$](/math_tex/bde5dbe480c8c635e666fd4b1d8b396482.gif)
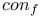
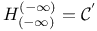
![${H^{(r, s)}_{(l)}}{[0]}$](/math_tex/997d9e64d15ac98326646c97de53d3d482.gif)
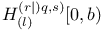
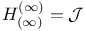
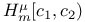
![${H^{\mu}}{[c_{1}, c_{2}]}$](/math_tex/01e5c8c615eb703be30ca50ae7fabd8d82.gif)

![${[ ]}_{(q)}$](/math_tex/d39919ca1d711895153c2de13a37054f82.gif)
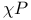
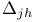
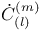
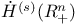
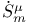
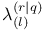
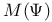
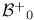
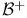
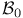

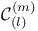 ,
, 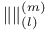
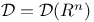
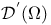

![${\mathcal{F}}{ _{[\omega]}}{\varphi}$](/math_tex/2d56de71be87d3695e9bd32c81cf67c582.gif)
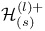
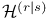
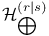
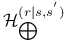
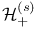 ,
, 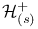
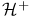
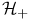 ,
, 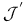
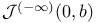
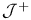
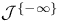
![${\mathcal{J}}^{{\{}m{\}}}_{[+]}$](/math_tex/ce0d48632f1c50ca042a25a5f33da7b382.gif) ,
, ![${\mathcal{J}}^{{\{}-{\infty}{\}}}_{[+1]}$](/math_tex/284a0ad8effab661a9514486b732f39e82.gif)
![${\mathcal{J}}_{[+]}$](/math_tex/4837890421af5ba9b9a45a1af5967b2682.gif)
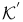
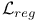
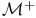 ,
, 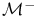
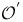
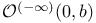
![${\mathcal{O}}^{{\{}-{\infty}{\}}}_{[+]}$](/math_tex/54a21d28255c4fc6144bdc7572c1079482.gif)
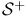
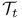
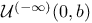
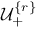 ,
, 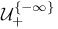
![${\mathcal{V}}^{(-{\infty})}_{[+]}$](/math_tex/c3ec73bc1d9d5118137b546849a2fadb82.gif) ,
, ![${\mathcal{W}}^{(-{\infty})}_{[+]}$](/math_tex/3eac6d553e16e758110bacbc45d3952582.gif)
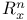
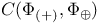
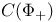
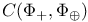
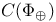

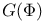

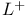
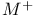
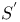
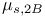
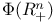
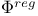
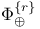 ,
, 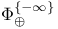
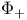 ,
, 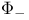
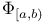 ,
, ![${\Phi}_{(a, b]}$](/math_tex/aae8cbcb9c4a5738c208b306f2ce2f1d82.gif)
![${\Phi}_{[\omega]}$](/math_tex/4c92a7a167312c8a015942b2d0d5414d82.gif)
![${\Phi}_{[\rho]}$](/math_tex/4cca30e7eee7c8778c12657ef5ea98d582.gif)
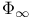 ,
, 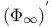
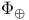
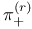
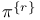
![${\Psi}^{[\omega]}$](/math_tex/33558302e511c9ddfa6f05d1e321459582.gif)
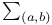 ,
, 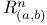
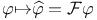
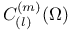 ,
, 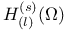
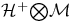 ,
, 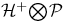
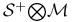
![${{\mid} {\mid}}^{(s)}_{(l)[\rho]}$](/math_tex/6585f2d7a1e8b472fbaad92ffdc0a1ff82.gif) ,
, ![${{\parallel} {\parallel}}^{(s)}_{(l)[\rho]}$](/math_tex/b52b64ad8895973d92b4356f8d78f50782.gif)
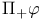
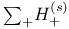
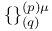
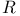 ), W(K)
), W(K) 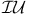 ,
, 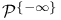
 в
в 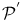 в
в 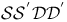
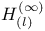 ]
]  ]
]