T-задача 71
V-альтернанс 95 241 242
Аппаратурная реализация функций 4
Аппроксимация кусочная 3 13—16
Аргумент в рациональной степени 122
Арктангенс 181
Арктангенс гиперболический 181
Асимптотически равномерное приближение сплайнами 39
Асимптотически равномерное приближение сплайнами в метрике 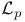 по по 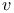 -й производной 110 -й производной 110
Асимптотически равномерное приближение сплайнами в метрике 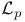 по по 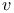 -й производной, погрешность 110 111 112 -й производной, погрешность 110 111 112
Асимптотически равномерное приближение сплайнами в метрике 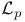 по по 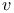 -й производной, уравнение для границ 111 112 113 -й производной, уравнение для границ 111 112 113
Асимптотически равномерное приближение сплайнами нелинейными чебышевскими, интерполяционными 116 117
Асимптотически равномерное приближение сплайнами нелинейными чебышевскими, непрерывными 115 116
Асимптотически равномерное приближение сплайнами нелинейными чебышевскими, разрывными 114
Асимптотически равномерное приближение сплайнами рациональными чебышевскими, интерполяционными 40
Асимптотически равномерное приближение сплайнами рациональными чебышевскими, непрерывными 40
Асимптотически равномерное приближение сплайнами рациональными чебышевскими, разрывными 40 69
Асимптотически равномерное приближение сплайнами рациональными чебышевскими, сравнение с равномерным приближением 65—69
Асимптотически равномерное приближение сплайнами рациональными чебышевскими, уравнение для границ 40 41
Баума гиперболический сплайн 142
Бернулли числа 180
Бернштейна формула 160
Бесселя функция модифицированная нулевого порядка 183
Бесселя функция модифицированная первого порядка 183 184
Бесселя функция нулевого порядка 182 183
Бесселя функция первого порядка 183 184
Валле-Пуссена алгоритм 74
Гамма-функция 178
Гиперболические функции 255
Границ звеньев определения алгоритмы Гребенникова 8 9
Границ звеньев определения алгоритмы Малоземова и Певного 9
Границ звеньев определения алгоритмы Мейнардуса 9 49
Границ звеньев определения алгоритмы при асимптотически равномерном приближении с заданной погрешностью 43 44
Границ звеньев определения алгоритмы при асимптотически равномерном приближении с заданным количеством звеньев 45
Границ звеньев определения алгоритмы при равномерном приближении 64
Границ звеньев определения алгоритмы при равномерном приближении ломаной 45—46
Границ звеньев определения алгоритмы при равномерном приближении отрезками постоянных 42 43
Границ звеньев определения алгоритмы при таблично равномерном приближении 50
Границ звеньев определения алгоритмы при таблично равномерном приближении с заданной погрешностью 58—61
Границ звеньев определения алгоритмы при таблично равномерном приближении с заданным количеством звеньев 61—64
Двух переменных функции 255
Дискретизация адаптивная 190—192
Дифференциальные уравнения 254
Замкнутых кривых равномерное приближение 8 255
Звеньев количество при равномерном приближении чебышевским рациональным сплайном, интерполяционным 25 27
Звеньев количество при равномерном приближении чебышевским рациональным сплайном, непрерывным 21 24 27
Звеньев количество при равномерном приближении чебышевским рациональным сплайном, разрывным 12
Звенья сплайна квазиравные 199—200
Звенья сплайна квазиравные, алгоритмы определения границ 201—205
Звенья сплайна равные 28—32 37 38
Интерполирование с переменной длиной звена 33
Интерполяционные чебышевские сплайны 7 25
Кельвина функция 184—186
Комплекс программ по наилучшему чебышевскому приближению функций 87—89
Корень s-й степени из многочлена 87—89
Косинус гиперболический 180
Косинуса при равномерном приближении многочисленными чебышевскими сплайнами, границы звеньев 177
Косинуса при равномерном приближении многочисленными чебышевскими сплайнами, погрешность, абсолютная 176 178
Косинуса при равномерном приближении многочисленными чебышевскими сплайнами, погрешность, относительная 177 179
Косинуса при равномерном приближении многочисленными чебышевскими сплайнами, ядро 177
Линейное программирование 4
Логарифмическая функция от многочлена 84 85
Логарифмическая функция от рационального многочлена, алгоритм построения 91
Логарифмическая функция от рационального многочлена, ядро 121
Логарифмической функции при приближении чебышевским рациональным сплайном, границы звеньев при равномерном приближении, абсолютном 168 172
Логарифмической функции при приближении чебышевским рациональным сплайном, границы звеньев при равномерном приближении, относительном 169
Логарифмической функции при приближении чебышевским рациональным сплайном, количество звеньев при равномерном приближении с заданной погрешностью, абсолютной 168 171
Логарифмической функции при приближении чебышевским рациональным сплайном, количество звеньев при равномерном приближении с заданной погрешностью, относительной 169
Логарифмической функции при приближении чебышевским рациональным сплайном, погрешность при равномерном приближении, абсолютном 167 171
Логарифмической функции при приближении чебышевским рациональным сплайном, погрешность при равномерном приближении, относительном 169 172
Логарифмической функции при приближении чебышевским рациональным сплайном, со звеньями равной длины погрешность, абсолютная 169
Логарифмической функции при приближении чебышевским рациональным сплайном, со звеньями равной длины погрешность, относительная 170
Логарифмической функции при приближении чебышевским рациональным сплайном, ядро 165 170
Ломаными приближение равномерное 13—16
Мейнардуса формула максимальной погрешности наилучшего чебышевского рационального приближения 10
Мейнардуса формула максимальной погрешности наилучшего чебышевского рационального приближения показательной функции 154
Многочлен наилучшего чебышевского приближения 3 4
Многочлен обобщенный по чебышевским системам функций 140
Многочлен по нечетным степеням аргумента 145
Многочлен по степеням 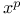 172—175 172—175
Многочлен по четным степеням аргумента 145
Многочлен рациональный 6
Многочлен умноженный на функцию 123
Многочлен Чебышева 160
Моделирование 254
Наилучшее 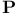 -приближение 206 -приближение 206
Наилучшее 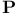 -приближение, чебышевское 207 -приближение, чебышевское 207
Наилучшее приближение, интегральное 255
Наилучшее приближение, средне-квадратическое 255
Наилучшее приближение, чебышевское 71 72
Наилучшее приближение, чебышевское, многочленное 71 72
Наилучшее приближение, чебышевское, нелинейное 71 73—79
Наилучшее приближение, чебышевское, рациональными многочленами 6
Наилучшее приближение, чебышевское, с двумя закрепленными точками 246
Наилучшее приближение, чебышевское, с закрепленными границами 116
Наилучшее приближение, чебышевское, с интерполированием в s внешних точках 244
Невязка 151
Нелинейное выражение от многочлена 84—87
Непрерывные чебышевские сплайны 7
Норма погрешности, 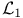 255 255
Норма погрешности, 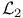 255 255
Норма погрешности, 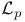 109 109
Норма погрешности, новая структура 152
Норма погрешности, чебышевская 6 192
Ньютона метод вычисления квадратного корня 151
Обменные теоремы о нелинейных приближениях, логарифмическом 91
Обменные теоремы о нелинейных приближениях, показательном 89
Обменные теоремы о нелинейных приближениях, степенном 92
Паде-сплайны 34—37
Пакета программ по наилучшему чебышевскому приближению функций, системное накопление 247
Пакета программ по наилучшему чебышевскому приближению функций, структура 247—249
Пакета программ по наилучшему чебышевскому приближению функций, функциональное накопление 247 249—253
Погрешность равномерного приближения функции нелинейным чебышевским сплайном 146—148
Погрешность равномерного приближения функции рациональным чебышевским сплайном, интерполяционным 25 27
Погрешность равномерного приближения функции рациональным чебышевским сплайном, непрерывным 24 27
Погрешность равномерного приближения функции рациональным чебышевским сплайном, разрывным 10 52—54
Погрешность равномерного приближения функции с помощью интерполирования с переменной длиной звена в виде 33
Погрешность равномерного приближения функции с помощью интерполирования с переменной длиной звена в виде отрезков ряда Тейлора 33
Погрешность равномерного приближения функции с помощью интерполирования с переменной длиной звена в виде сплайна Паде 36
Погрешность равномерного приближения функции с помощью интерполирования с переменной длиной звена в виде эрмитового сплайна 32
Поиск ближайшего 195
Показательная функция от многочлена 84 85 90
Показательная функция от рационального многочлена, алгоритм построения 89
Показательная функция от рационального многочлена, ядро 120
Показательной функции при приближении чебышевским рациональным сплайном, границы звеньев при равномерном приближении, абсолютном 156
Показательной функции при приближении чебышевским рациональным сплайном, границы звеньев при равномерном приближении, относительном 157
Показательной функции при приближении чебышевским рациональным сплайном, количество звеньев при равномерном приближении с заданной погрешностью, абсолютной 155
Показательной функции при приближении чебышевским рациональным сплайном, количество звеньев при равномерном приближении с заданной погрешностью, относительной 157
Показательной функции при приближении чебышевским рациональным сплайном, погрешность при равномерном приближении, абсолютном 154
Показательной функции при приближении чебышевским рациональным сплайном, погрешность при равномерном приближении, относительном 157
Показательной функции при приближении чебышевским рациональным сплайном, со звеньями равной длины погрешность, абсолютная 156
Показательной функции при приближении чебышевским рациональным сплайном, со звеньями равной длины погрешность, относительная 158
Показательной функции при приближении чебышевским рациональным сплайном, ядро 152
Понижения метод 243
Постоянных отрезками равномерное приближение, абсолютное 13 14
Постоянных отрезками равномерное приближение, относительное 14—16
Похгаммера символ 124 159
Приближение сплайнами, асимптотически равномерное 39
Приближение сплайнами, неравномерное 198
Приближение сплайнами, равномерное 7
Приближение сплайнами, таблично равномерное 51
Программная реализация вычислительных алгоритмов 5 239
Производных приближение с помощью сплайнов, чебышевских многочленных, интерполяционных 227—229
Производных приближение с помощью сплайнов, чебышевских многочленных, непрерывных 227
Производных приближение с помощью сплайнов, чебышевских многочленных, разрывных 223—226
Производных приближение с помощью сплайнов, чебышевских многочленных, эрмитовых многочленных 230—234
Производных приближение с помощью сплайнов, чебышевских многочленных, эрмитовых рациональных 235—238
Процессор с неравными интервалами 193—197
Равномерное приближение сплайнами в метрике 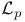 109—114 109—114
Равномерное приближение сплайнами интегральными 255
| Равномерное приближение сплайнами многочленными 8—10
Равномерное приближение сплайнами многочленными, с заданной погрешностью 8
Равномерное приближение сплайнами многочленными, с заданным количеством звеньев 9
Равномерное приближение сплайнами набора функций, алгоритм построения 217
Равномерное приближение сплайнами набора функций, количество вычислений 217—218
Равномерное приближение сплайнами набора функций, погрешность 218—220
Равномерное приближение сплайнами со звеньями разного вида 205
Равномерное приближение сплайнами среднеквадратическими 255
Равномерное приближение сплайнами чебышевскими нелинейными, аналитических функций 114—120
Равномерное приближение сплайнами чебышевскими нелинейными, непрерывных функций 150
Равномерное приближение сплайнами чебышевскими нелинейными, функций, заданных в виде таблиц 146
Равномерное приближение сплайнами чебышевскими рациональными 65—69
Равномерное приближение сплайнами чебышевскими рациональными, выбор вида сплайна 186
Равномерное приближение сплайнами чебышевскими рациональными, с заданной погрешностью 7
Равномерное приближение сплайнами чебышевскими рациональными, с заданным количеством звеньев 7 10
Разрядность 152
Рациональный многочлен 6
Рациональный многочлен для приближения нечетных функций 145
Рациональный многочлен наилучшего чебышевского приближения 6
Рациональный многочлен наилучшего чебышевского приближения, с s закрепленными точками 6
Рациональный многочлен наилучшего чебышевского приближения, с закрепленной левой границей 6
Рациональный многочлен наилучшего чебышевского приближения, с интерполированием 6
Рациональный многочлен по четным степеням аргумента 145
Рациональный многочлен умноженный на функцию 124
Ремеза алгоритм 72—73 239
Сигнал 3 8
Синус гиперболический 179 180
Синуса при равномерном приближении многочленными чебышевскими сплайнами, границы звеньев 176
Синуса при равномерном приближении многочленными чебышевскими сплайнами, погрешность, абсолютная 176 178
Синуса при равномерном приближении многочленными чебышевскими сплайнами, погрешность, относительная 176 179
Синуса при равномерном приближении многочленными чебышевскими сплайнами, ядро 177
Спецпроцессор 255
Сплайны,  8 8
Сплайны, гладкие нелинейные 254
Сплайны, интегральные 255
Сплайны, негладкие 4
Сплайны, с непрерывной первой производной 254
Сплайны, чебышевские 7 32
Сплайны, эрмитовые 32 38
Станки с числовым программным управлением 4 254
Степенная функция от многочлена 85
Степенная функция от рационального многочлена, алгоритм построения 92
Степенная функция от рационального многочлена, ядро 122
Степенной функции при приближении чебышевским рациональным сплайном, границы звеньев при равномерном приближении, абсолютном 161 162
Степенной функции при приближении чебышевским рациональным сплайном, границы звеньев при равномерном приближении, относительном 163 164
Степенной функции при приближении чебышевским рациональным сплайном, количество звеньев при равномерном приближении с заданной погрешностью, абсолютной 161
Степенной функции при приближении чебышевским рациональным сплайном, количество звеньев при равномерном приближении с заданной погрешностью, относительной 163
Степенной функции при приближении чебышевским рациональным сплайном, погрешность при равномерном приближении, абсолютном 159
Степенной функции при приближении чебышевским рациональным сплайном, погрешность при равномерном приближении, относительном 163
Степенной функции при приближении чебышевским рациональным сплайном, со звеньями равной длины погрешность, абсолютная 162
Степенной функции при приближении чебышевским рациональным сплайном, со звеньями равной длины погрешность, относительная 165
Степенной функции при приближении чебышевским рациональным сплайном, ядро 158
Сумма многочлена и гиперболических синуса или косинуса 104—106
Сумма многочлена и гиперболических синуса или косинуса, с аддитивным параметром 106
Сумма многочлена и двух нелинейных функций 107
Сумма многочлена и двух экспонент 108
Сумма многочлена и логарифма, алгоритм определения параметров 102—104
Сумма многочлена и логарифма, характеристическая теорема 101
Сумма многочлена и логарифма, ядро 128
Сумма многочлена и нелинейной функции, теорема Вейерштрасса 93
Сумма многочлена и нелинейной функции, характеристическая теорема 93—95
Сумма многочлена и нелинейной функции, ядро 117
Сумма многочлена и однопараметрической нелинейной функции 134
Сумма многочлена и степени, алгоритм определения параметров 99
Сумма многочлена и степени, характеристическая теорема 98
Сумма многочлена и степени, ядро 127
Сумма многочлена и трехпараметрического, гиперболического синуса или косинуса 132—134
Сумма многочлена и трехпараметрического, степенного выражения 129
Сумма многочлена и функции с двумя нелинейными параметрами 107
Сумма многочлена и экспоненты, алгоритм определения параметров 97
Сумма многочлена и экспоненты, характеристическая теорема 96
Сумма многочлена и экспоненты, ядро 127
Сумма степеней 143
Сумма экспонент 141
Таблиц, память 193 194
Таблиц, сокращенных использование 195—196
Таблица Паде 36
Тангенс 180 181
Тангенс гиперболический 181
Тейлора ряд 33 196
Тейлора формула 33
Тейлора — Эйткена формула 34
Теслера методы разложения функций по невязкам 151
Теслера методы рекуррентных соотношений 152
Тиле цепная дробь 34
Узлов сплайнов расположение при асимптотически равномерном приближении косинуса 177
Узлов сплайнов расположение при асимптотически равномерном приближении косинуса, гиперболического 180
Узлов сплайнов расположение при асимптотически равномерном приближении логарифма с погрешностью, абсолютной 168 172
Узлов сплайнов расположение при асимптотически равномерном приближении логарифма с погрешностью, относительной 169
Узлов сплайнов расположение при асимптотически равномерном приближении показательной функции с погрешностью, абсолютной 156
Узлов сплайнов расположение при асимптотически равномерном приближении показательной функции с погрешностью, относительной 157
Узлов сплайнов расположение при асимптотически равномерном приближении синуса 176
Узлов сплайнов расположение при асимптотически равномерном приближении синуса, гиперболического 179
Узлов сплайнов расположение при асимптотически равномерном приближении степенной функции с погрешностью, абсолютной 161 162
Узлов сплайнов расположение при асимптотически равномерном приближении степенной функции с погрешностью, относительной 163 164
Узлов сплайнов расположение при асимптотически равномерном приближении функции Кельвина 7
Узлов сплайнов расположение при асимптотически равномерном приближении функции Кельвина, bei 185 186
Узлов сплайнов расположение при асимптотически равномерном приближении функции Кельвина, ber 184
Узлов сплайнов расположение при асимптотически равномерном приближении функции, разлагаемой в ряд по степеням 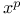 173 174 173 174
Узлов сплайнов распределение 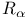 -оптимальное 46 -оптимальное 46
Узлов сплайнов распределение 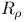 -оптимальное 47 -оптимальное 47
Узлов сплайнов распределение оптимальное 7 109
Узлов сплайнов распределение оптимальное, по Мейнардусу 49
Узлов сплайнов распределение оптимальное, по формуле прямоугольников 47 48
Узлов сплайнов распределение оптимальное, с одновременным нахождением 48
Функции от многочленов, теоремы Вейерштрасса 84
Функции от многочленов, характеристическая теорема 85
Функции от многочленов, чебышевская интерполяция 86
Функции от многочленов, ядра 120—122
Функции от рациональных многочленов 89
Функции, представляемые степенными рядами и приближаемые многочленными чебышевскими сплайнами, границы звеньев 173—175
Функции, представляемые степенными рядами и приближаемые многочленными чебышевскими сплайнами, погрешность, абсолютная 173—174
Функции, представляемые степенными рядами и приближаемые многочленными чебышевскими сплайнами, погрешность, относительная 175
Функции, представляемые степенными рядами и приближаемые многочленными чебышевскими сплайнами, ядро 173
Функциональные преобразователи информации 198
Хевисайда функция 7
Цепная дробь Тиле 34
Чебышева многочлены 160
Чебышевский 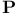 -сплайн границы звеньев при асимптотически равномерном приближении 209 -сплайн границы звеньев при асимптотически равномерном приближении 209
Чебышевский 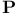 -сплайн погрешность равномерного приближения 207—209 -сплайн погрешность равномерного приближения 207—209
Чебышевский 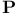 -сплайн таблично равномерное приближение, с заданной погрешностью 210—212 -сплайн таблично равномерное приближение, с заданной погрешностью 210—212
Чебышевский 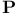 -сплайн таблично равномерное приближение, с заданным количеством звеньев 213 -сплайн таблично равномерное приближение, с заданным количеством звеньев 213
Чебышевский 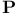 -сплайн таблично равномерное приближение, с фиксированными узлами 214 -сплайн таблично равномерное приближение, с фиксированными узлами 214
Чебышевский альтернанс 74 95
Чебышевский сплайн рациональный 7
Чебышевский сплайн рациональный, интерполяционный 7 25 26 27 32
Чебышевский сплайн рациональный, непрерывный 7 21—24 26
Чебышевский сплайн рациональный, разрывной 7 10 32
Чебышевский сплайн с квазиравными звеньями 198—200
Чебышевский сплайн с квазиравными звеньями, увеличивающимися 201—205
Чебышевский сплайн с малым количеством параметров 241
Чебышевский сплайн с равными звеньями 28—32
Экономичные приближения 254
Экспериментальные исследования 255
Экспоненциально-степенное приближение, относительное 82
Экспоненциально-степенное приближение, теорема Вейерштрасса 80
Экспоненциально-степенное приближение, характеристическая теорема 80
Экспоненциально-степенное приближение, чебышевская интерполяция 81
Экспоненциально-степенное приближение, экономия времени счета 83
Экспоненциально-степенное приближение, ядро 136
Экспоненциальное приближение см. "Показательная функция"
Эллиптический интеграл Лежандра первого рода 101
Ядер свойства 117—119
Ядро приближения функции с помощью аргумента в рациональной степени 122
Ядро приближения функции с помощью логарифмической функции от рационального многочлена 121
Ядро приближения функции с помощью многочлена 12
Ядро приближения функции с помощью многочлена, по нечетным степеням аргумента 145
Ядро приближения функции с помощью многочлена, по степеням 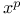 143—145 143—145
Ядро приближения функции с помощью многочлена, по четным степеням аргумента 145
Ядро приближения функции с помощью многочлена, умноженного на функцию 123
|
 |
|
О проекте
|
|
О проекте



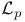 по
по 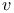 -й производной
-й производной 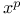
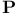 -приближение
-приближение 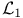
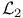

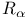 -оптимальное
-оптимальное 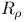 -оптимальное
-оптимальное