Авторизация
Поиск по указателям
Александров П.С., Ефремович В.А. — Очерк основных понятий топологии
Обсудите книгу на научном форуме Нашли опечатку?
Название: Очерк основных понятий топологииАвторы: Александров П.С., Ефремович В.А. Аннотация: Настоящее издание представляет собой значительно расширенный перевод книги проф. МГУ П. С. Александрова «Простейшие основные понятия топологии», вышедшей в 1932 г. на немецком языке. Кроме некоторых изменений и дополнений к тексту немецкого издания заново написана проф. В. А. Ефремовичем глава о замкнутых поверхностях. Книга снабжена предисловием известного немецкого математика Д. Гильберта.
Язык: Рубрика: Математика /Серия: Сделано в холле Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1936Количество страниц: 94Добавлена в каталог: 26.08.2009Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
70 Betti, группы 56 57 87—91 Betti, группы по модулю 2 62 Betti, полные группы 56 57 Betti, приведенные (свободные) группы 56 57 Betti, числа 57 60 87—91 Betti, числа по модулю 2 62 Euler'ова характеристика комплекса 58, ее инвариантность 80 Euler'ова характеристика поверхности 27 Lebesgue'ово число покрытия 77 Аксиомы Hausdorff'а 41—42 Алгебраический комплекс 49—50 51 52 Алгебраический комплекс по модулю 2 61 Алгебраический комплекс, абстрактный 75 Алгебраический комплекс, области коэффициентов 63 Алгебраический подкомплекс геометрического комплекса 51 Барицентрическая звезда 73 Барицентрическая звезда, центр 73 Барицентрические координаты 82 Внутренняя точка 10 Геометрический комплекс 39 40 52 61 Геометрический комплекс, абстрактный 75 Гомеоморфные множества 8 Гомологий классы 55 Гомология, сильная 55 Гомология, слабая 55 Граница ориентированного комплекса 48 Граница ориентированного симплекса 46 52 Граница, алгебраического комплекса 52 Граница, комплекса по модулю 2 61 Группа кручения 87 89 Группы 54 Группы 55 Группы 51 Группы 62 Группы 53 Делитель границы 55 Замкнутая неориентируемая поверхность 19 38 Замкнутая неориентируемая поверхность, Euler'ова характеристика 37 62 Замкнутая неориентируемая поверхность, модель 34—37 Замкнутая ориентируемая поверхность 33 37 49 53 87 Замкнутая ориентируемая поверхность, Euler'ова характеристика 33 62 Замкнутая ориентируемая поверхность, Klein'ова нормальная форма 11 33 Замкнутая ориентируемая поверхность, канонические разрезы 34 Замкнутая ориентируемая поверхность, порядок связности 33 Замкнутая поверхность 15 Замкнутая поверхность, классификация 32—38 Замкнутая поверхность, полная система топологических инвариантов 38 Замкнутое n-мерное многообразие 40 42—43 53 Звезда, вершины в комплексе 15 Звезда, линейная 20 Звезда, циклическая 15 Изолированная вершина 13 Изолированное ребро 14 Комплекс, r-мерный 40 Комплекс, двумерный 14 Комплекс, линейный 13 Комплекс, неполный 14 Комплекс, нульмерный 13 Комплекс, ориентированный 47 Комплекс, связный 14 Компоненты комплекса 14 Край поверхности 21 Лемма, Lebesgue'а 77—78 Лемма, Sperner'а 71—72 Линейный комплекс, Euler'ова характеристика 26 Линейный комплекс, порядок связности 25 60 Множество, дополнительное 10 Множество, замкнутое 10 Множество, ограниченное 9 Множество, открытое 10 Неориентируемая поверхность 19 23—25 Неориентируемое замкнутое многообразие 89 Неподвижная точка отображения 9 Нерв системы множеств 74 Окрестность 40 41 Ориентация 18 Ориентируемая поверхность 19 Ориентируемое замкнутое многообразие 53 80 89 Отображение взаимнооднозначное 8 Отображение во множество 7 Отображение на множество 7 Отображение непрерывное 7 42 Отображение топологическое 8 Поверхность Moebius'а 22 24 28 35 36 37 41 49 Поверхность с краем 20 Поверхность с краем, полная система топологических инвариантов 38 Подразделение, алгебраического подкомплекса геометрического комплекса 63—64 Подразделение, барицентрическое 72 Подразделение, геометрического комплекса 63 Подразделение, правильное двумерного комплекса 17 Подразделение, элементарное двумерного комплекса 17 Подчиненные элементы 13 14 Полиедр 39 40 52 Порядок конечной системы множеств 70 Порядок связности поверхности 26 27 Предельная точка 9 Проективная плоскость 19—20 24—25 41 49 54 57 62 63 Проекционный спектр 76 Простая поверхность 28 Простая поверхность, Euler'ова характеристика 31—32 Простая поверхность, классификация 29—31 Простая поверхность, нормальная форма 31 Простая поверхность, порядок связности 32 Пространство, Hausdorff'а 41 Пространство, топологическое 41 Размерность 72 84 Разрез замкнутый 28 Разрез, двубережный 22 Разрез, однобережный 22 Разрезывание поверхности 24 Род поверхности 11 27 33 Симплекс 39 Симплекс, грань 39 Симплекс, ориентированный 46 50 Симплекс, размерность 39 Симплициальная аппроксимация непрерывного отображения 67 84 Симплициальное отображение 67—68 Теорема Brouwer'а о неподвижных точках 82—83 Теорема Brouwer'а об инвариантности числа измерений 40 66 72—74 Теорема Jordan'а n-мерная 90 Теорема Weierstrass'а 9 Теорема двойственности, Alexander'а 89 90 Теорема двойственности, Poincare 88—89 90 Теорема инвариантности групп Betti 67 77—80 Теорема консервативности границ 68 Теорема мостовых 70—72 Теорема об 84—86 Теоремы консервативности 68—69 Топологические свойства 8 Топологический инвариант 18 Топологическое перемножение 43—44 Тор 11 28 34 43 44 Триангуляция поверхности 15 Фигура геометрическая 7 65 Формула, Euler'а 27 Формула, Euler'а — Poincare 58 62 Цикл 52 Цикл, ограничивающий 53 54 Элементарные поверхности 11 «Вывернутая ручка» 34—35
Реклама
-покрытие замкнутого множества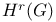 
, 
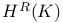ограничивающих циклов 
, 
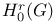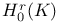делителей границ 
, 
, 
, 
, 
, 
, 
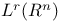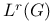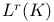
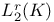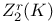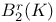
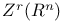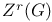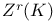циклов 
|
|
О проекте