|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Полак Э. — Численные методы оптимизации. Единый подход |
|
|
 |
| Предметный указатель |
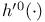 , , 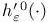 , , 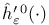 , , 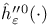 218 218
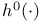 187 187
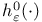 194 195 194 195
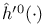 , , 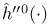 220 220
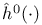 209 209
 207 207
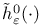 205 205
 -активное множество индексов 195 -активное множество индексов 195
 -дробление 200 -дробление 200
Абрамов, А.А. 110 113 138 364
Абстрактная проблема 29
Авдеева, Л.И. 33 366
Акилов, Г.П. 57 133 366
Алгоритм декомпозиции 195 209
Алгоритм декомпозиции двойственный 250
Алгоритм декомпозиции прямого типа 275 279 283
Алгоритм наискорейшего спуска 46 57
Алгоритм наискорейшего спуска модифицированный 60
Алгоритм наискорейшего спуска, реализуемая модификация 50
Алгоритм Полака — Рибьера 74 88 101 286 303
Алгоритм Полака — Рибьера, рекомендуемая реализация 351
Алгоритм с переменной метрикой (Дэвидона — Флетчера — Пауэлла) 77 88 314
Алгоритм с переменной метрикой, рекомендуемая реализация 353
Алгоритм Флетчера — Ривса 73 88 100 312
Алгоритмы двойственные 247
Алгоритмы нестационарные 38
Алгоритмы по выбору шага 49 54 56
Алгоритмы принципиальные 27
Алгоритмы прямые 247
Алгоритмы реализуемые 27
Алгоритмы стационарные 38
Антосиевич, Г.А. 57 364
Армийо, Л. 55 364
Балакришнан, А.В. 182 364
Баничук, Н.В. 63 364 369
Барр, Р.О. 279 364
Барьерные методы (методы внутренних штрафных функций) 155
Беллман, Р. 107 111 129 132 135 364
Берж, С. 339 364
Болтянский, В.Г. 26 368
Буй-Тронг Ли 183 184 191 364
Бюси, Р.С. 149 364
Ван-Слайк, Р.М. 195 249 364
Варайя, П.П. 33 364
Вейнотт, А. 33 193 194 368
Версия ЗПП 208
Восстановление 87
Вторая производная 339
Ву, Ф. 10
Вулф, П. 194 247 279 364 368
Вычисление градиентов в задачах дискретного оптимального управления 88—91
Вычисление градиентов в задачах непрерывного оптимального управления 96—98
Гамкрелидзе, Р.В. 26 368
Гермейер, Ю.Б. 155 364
Гибридный метод (объединение метода возможных направлений с методом штрафных функций) 211
Гибридный метод проекции градиента 241
Гилберт, Е.Г. 10 279 364 365
Гирсанов, И.В. 21 365
Голдштейн, А.А. 51 55 58 61 299 300 365
Градиент 96
Градиентные методы 346
Градиентный метод для задачи непрерывного оптимального управления 98
Градиентный метод рекомендуемый 349
Градиентный метод с аппроксимацией производных 60
Градиентный метод с выбором величины шага по методу золотого сечения 50
Гросс, Г. 10
Гудмен, Т.Р. 107 109 129 132 365
Гуленко, В.П. 216 365
Гурвиц, Л. 33 369
Данилин, Ю.М. 55 77 365
Данциг, Дж.Б. 195 249 364
Демьянов, В.Ф. 154 365
Депари, М. 260 367
Джон, Ф. 22 365
Диада 78
Дискретизация задач непрерывного оптимального управления 18—20
Дроби Фибоначчи 49
Дубовицкий, А.Я. 21 365
Дьёдонне, Дж. 96 338 365
Дэвидон, В.С. 77 314 365
Дэниел, Дж.В. 80 303 365
Елкин, Р.М. 63 65 365
Еремин, И.И. 154 155 365
Ермольев, Ю.М. 216 365
Желательные точки 29
Задача геометрическая 276
Задача геометрическая, алгоритм 279
Задача двойственная 247 257
Задача двойственная, алгоритм 260 267 270
Задача дискретного оптимального управления 15
Задача дискретного оптимального управления, формы записи в терминах задачи нелинейного программирования 17
Задача квадратичного программирования 264 265 282
Задача на быстродействие 270
Задача нелинейного программирования 15
Задача непрерывного оптимального управления 16
Задача непрерывного оптимального управления с фиксированным временем 94
Задача непрерывного оптимального управления со свободным временем 94
Задача о минимуме энергетических затрат 273
Задача прямая 247 253
Закон управления с обратной связью 126
Зангвилл, В.И. 10 32 33 155 365 367
Застревание алгоритма 194
Зойтендейк, Г. 22 33 69 193—196 205 365
Зуховицкий, С.И. 33 193 205 206 366
Исааксон, И. 297 366
Итон, Дж.Г. 260 366
Калаба, Р. 107 111 129 135 364
Калфонд, П. 240 366
Канторович, Л.В. 57 133 366
Карри, Х. 57 366
Касательное отображение 255
Квадратичная целевая функция в задаче дискретного оптимального управления 125
Квадратичная целевая функция в задаче непрерывного оптимального управления 149
Квазилинеаризация 107 111 132—135
Квазиньютоновский алгоритм 58
Квазиньютоновский алгоритм модифицированный 61
Квазиньютоновский метод 349
Квазиньютоновский метод рекомендуемый 350
Келлер, Г.Б. 297 366
Кеннет, Ф. 107 111 129 132 135 366
Клессиг, Р. 10 40 329 330 351 352 366
Козн, А. 10 62 303 312 313 366
Коши, А.Л. 57 366
Краевые задачи 106
Красовский, Н.Н. 260 366
Куллум, Дж. 180 181 366
Куллум, К.Д. 9 17 21 22 25 26 58 207 211 247 249 250 356 366
Кун, Х.В. 22 24 77 366
Курант, Р. 155 366
Кэнон, М.Д. 9 17 21 22 25 26 58 207 211 247 249 250 356 366
Ланс, Г.Н. 107 109 129 132 365
Левитин, Е.С. 33 366
Ли, Г.С. 107 366
Лутсма, Ф.А. 155 355 366
Любич, Ю.И. 65 366
Майстровский, Г.Д. 65 366
Мак-Джилл, Р. 107 111 129 132 135 366
Мак-Кормик, Г.П. 155 169 170 355 367 368
Мангасарьян, О.Л. 22 251 367
Матрица вторых производных для задачи оптимального управления 92
Мейер, Г. 10 33 279 337 367
| Мейер, Г.Е. 78 79 367
Мейн, Д.К. 59 367
Мессерли, Е.Дж. 10
Метод Абрамова 110 113—116 136—140 145
Метод возможных направлений 193
Метод возможных направлений в задачах с ограничениями типа равенств 210
Метод возможных направлений в оптимальном управлении 212
Метод возможных направлений второго порядка 217
Метод возможных направлений Зойтендейка 196
Метод возможных направлений Зуховицкого — Поляка — Примака 206
Метод возможных направлений Полака 198
Метод возможных направлений рекомендуемый, с квадратичным поиском 362
Метод возможных направлений рекомендуемый, с линейным поиском 359 361
Метод возможных направлений Топкиса — Вейнотта 194
Метод Гаусса — Зейделя 63 65
Метод Гудмена — Ланса 107 109 129—132
Метод локальных вариаций 62 63
Метод Ляпунова 32
Метод Ньютона — Рафсона 57 58 104 107 109 117 129 286
Метод Ньютона — Рафсона в банаховом пространстве 132
Метод проекции градиента 222 228
Метод проекции градиента для задач оптимального управления 244—246
Метод проекции градиента элементарный 229
Метод проекции градиента, ускоренная версия 239
Метод сопряженных градиентов 351
Метод сопряженных градиентов прототип 67
Метод сопряженных градиентов, вычислительные аспекты 87
Метод сопряженных градиентов, постановка задачи 66
Метод центров 183 184
Метод центров модифицированный 188
Метод центров модифицированный, реализация 192 337
Метод штрафных функций внешних 154 156
Метод штрафных функций внешних модифицированный 171
Метод штрафных функций внутренних 155 162
Метод штрафных функций внутренних модифицированный 175
Метод штрафных функций комбинированный (смешанный) 155 166
Метод штрафных функций комбинированный рекомендуемый 355
Метод штрафных функций комбинированный рекомендуемый с подпроцедурой сопряженных градиентов 357
Метод штрафных функций, вычислительные аспекты 168
Милютин, А.А. 21 365
Мищенко, Е.Ф. 26 368
Модель алгоритма 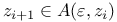 , , 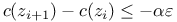 35 35
Модель алгоритма 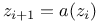 , , 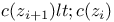 29 29
Модель алгоритма 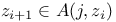 , , 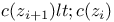 335 335
Модель алгоритма 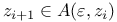 , , 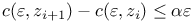 329 329
Модель алгоритма 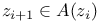 , , 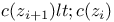 31 31
Модель алгоритма 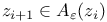 , , 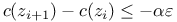 33 33
Модель алгоритма нестационарной версии методов возможных направлений 40
Моисеев, Н.Н. 7 113 182 367
Нахождение корней 104
Нейштадт, Л.В. 260 367
Норма Фробениуса 325
Островский, А.М. 293 367
Пауэлл, М.Дж.Д. 10 64 77—80 87 314 315 318 325 327 367 368
Петров, В.М. 63 364
Пиронно, О. 10
Поиск по методу золотого сечения 49 192 336
Полак, Э. 5—7 9 17 21 22 25 26 33 50 58 60 61 74 88 171 175 192 198 207 211 227 228 240 241 247 249 250 260 267 270 279 303 329 335 337 351 352 356 366 367
Поляк, Б.Т. 33 65 77 154 155 366—368
Поляк, Р.А. 193 205 206 366
Понтрягин, Л.С. 26 368
Правило остановки 29
Прайс, Дж.Ф. 61 365
Примак, М.Е. 193 205 206 366
Принцип максимума Понтрягина 26
Пропой, А.И. 25 216 368
Процесс биортогонализации 69
Пшеничный, Б.Н. 21 55 65 154 251 365 368
Разумихин, Б.С. 155 368
Рассел, Д.Л. 180 181 368
Расширенная задача оптимального управления 181
Рафель Дж. 10
Решение допустимое 21
Решение оптимальное 21
Рибьер, Г. 74 240 303 366 367
Ривс, К.М. 73 312 368
Розен, Дж.Б. 227 231 232 240 368
Рокафеллар, Р.Т. 251 368
Рубинов, А.М. 154 365
Сведение задачи со свободным временем к задаче с фиксированным временем 94
Скорость сходимости для алгоритма с переменной метрикой 314 324
Скорость сходимости для квазиньютоновского алгоритма 299 300
Скорость сходимости для метода Ньютона — Рафсона 294 300
Скорость сходимости для метода сопряженных градиентов 303
Скорость сходимости для модифицированного метода наискорейшего спуска 291 292
Соньо, Дж.К. 240 366
Споерл, Дж. 10
Степень обусловленности 346
Сходимость квадратичная 297
Сходимость линейная 285
Сходимость по крайней мере линейная 285
Сходимость сверхлинейная 294 297
Таккер, А.В. 22 24 77
Теорема о среднем 338
Теорема о среднем обобщенная 338
Теорема сходимости для алгоритма Полака — Рибьера 75
Теорема сходимости для алгоритма Флетчера — Ривса 74
Теорема сходимости для градиентных методов 47 52
Теорема сходимости для метода локальных вариаций 64
Теорема сходимости для метода переменной метрики 79—87
Теорема сходимости для модели алгоритма 30 31 35 38 40 44 45 332 335
Теорема сходимости для прототипа метода сопряженных градиентов 67 69
Топкис, Д.М. 33 194 368
Трауб, Дж.Ф. 368
Тремольер, Р. 184 368
Удзава, Х. 33 369
Уравнение Риккати в задачах дискретного оптимального управления 123—128
Уравнение Риккати в задачах непрерывного оптимального управления 147—153
Условия оптимальности для задачи дискретного оптимального управления 25
Условия оптимальности для задачи нелинейного программирования 21—25 104 186 206 227
Условия оптимальности для задачи непрерывного оптимального управления 26
Условия регулярности Куна — Таккера 207 211 356 357 361 362
Федоренко, Р.П. 368
Фиакко, А.В. 155 169 170 355 368
Флетчер, Р. 73 77 78 87 312 314 368
Формула Тейлора для разложений второго порядка 339
Формула Тейлора для разложений первого порядка 338
Франк, М. 279 368
Фромовиц, С. 367
Функция выпуклая 339
Функция выпуклая строго 340
Функция индексная 331
Функция итерационная Ньютона — Рафсона 57
Функция поиска 29
Функция прерывания 335
Функция расстояния 168 184 191
Халкин, Х. 10
Харт, Дж. 33 368
Хестенс, М.Р. 66 70 368
Хьюард, П. 10 183 184 186 188 191 364 369
Черноусько, Ф.Л. 63 364 369
Шерюоль, У. 63 369
Шор, Н.3. 77 369
Штифель, Е. 66 368
Штрафные функции 154
Штрафные функции в оптимальном управлении 176—183
Штрафные функции внешние 156
Штрафные функции внутренние 163
Эрроу, К. 33 369
Якобсон, Д.Х. 10
Ярасасингам, К. 10
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



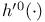 ,
, 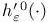 ,
, 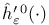 ,
, 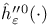
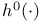
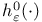
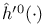 ,
, 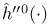
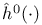

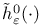
 -активное множество индексов
-активное множество индексов 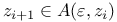 ,
, 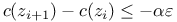
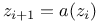 ,
, 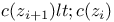
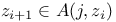 ,
, 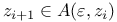 ,
, 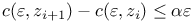
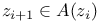 ,
,  ,
,