|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Аракелян Н.У., Мартиросян В.А. — Степенные ряды: аналитическое продолжение и локализация особенностей |
|
|
 |
| Предметный указатель |
Абель (Abel, N.) 5 6
Адамар (Hadamard, J.) 6 14 19 28 36 57 59 60 68
Адамаровская композиция (произведение) элементов гл.1 § 3.1
Алгебраическая функция гл.2 § 1.1
Аналитическая функция гл.1 §
Аналитический элемент (элемент) гл.1 § 2.1
Аналитическое продолжение элементов гл.1 § 2.1
Аналитическое продолжение элементов вдоль пути гл.1 § 2.1
Бесконечная матрица гл.1 § 6.1
Бибербах (Bieberbach, L.) 20 60 70
Боас (Boas, R.P.) 70
Борель (Borel, E.) 22 33 51 59 65
Вейерштрасс (Veierstress, K.) 5 11 13 14 15 58
Верхняя плотность гл.2 §
Ветвь аналитической функции гл.1 § 2.1
Виванти (Vivanti, G.) 61 66
Вигерт (Wigert, S.) 21 3
Внутренний экспоненциальный тип гл.1 § 5.1 5
Вольтерра (Volterra, V.) 12
Ганкель (Hankei, H.) 24 26 30
Гаусс (Gauss, C.P.) 5 10
Дарбу (Darboux, G.) 68
Деланж (Delange, H.) 68 74 75 79
Динс (Dienes, P.) 58
Дюфренуа (Dufresnoy, J.) 34
Звезда гл.1 § 3.1
Звезда (Миттаг — Леффлера) элемента гл.1 § 3.1
Звезда (спиральная) гл.1 § 3.1
Звезда (спиральная) элемента гл.1 § 3.1
Илиев (Ilieff, L.) 70
Индикаторная диаграмма гл.1 § 5.3
Индикатрисса гл.1 § 3.2; 5.3
Карлеман (Carleman, T.) 26
Карлсон (Carleson, P.) 21 32 35 40 48
Клаус (Claus, H.) 70
Конечного экспоненциального типа целая функция гл.1 § 3.2
Коши (Cauchy, A.) 5 6 7 10 20 22
Коэффициенты степенного рада гл.1 §
Критерий особой точки гл.1 § 2.1; § 1.2
Критерий рациональности Кронекера гл.2 § 1.1
Критерий регулярности дуги гл.2 §1 1.2
Критерий регулярности точки гл.2 § 1.2
Кронекер (Kronecker, L.) 56 58
Круг мероморфности степенного рада гл.2 § 1.1
Круг сходимости степенного рада гл.1 §
Лагранж (Lagrange, L.) 5
Лакунарный степенной рад гл.2 § 1.2
Лакуны гл.2 § 1.2; 3.1
Лакуны Адамара гл.2 § 1.2
Лакуны Фабри гл.2 §
Ле Руа (be Roy, E.) 15 21 28 29 53
Лебег (Lebesgue, H.) 23
Лерх (Lerch, M.) 59
Леш (Loesch, F.) 70
Линделёф (Lindeloef, E.) 21 25 26 29 30 53 55 60
Лиувилль (Liouville, J.) 13 21
Ло (Leau, L.) 21 28 31 61
Логарифмическая диаграмма гл.1 § 5.3
Логарифмически выпуклый компакт гл.1 § 5.3
Локализация особенностей гл.2
Локально-конечный экспоненциальный тип гл.1 § 5.3
Лоран (Laurent, P.) 26
Мажорантная функция степенного ряда гл.2 § 3.2
Маклорен (Maclaurin, C.) 5
Максимальная плотность гл.2 §
Манделъбройт (Mandelbrojt, J.) 61 67 68
Меромрфная в круге функция гл.2 § 1.1
| Метод переразложения гл.1 § 2.1
Метод функции коэффициентов гл.1 § 2.2
Методы Ле Руа, Линделёфа, Миттаг — Леффлера гл.1 § 6.1
Методы суммирования гл.1 § 2.2; 6.1
Минковский (Minkowski, H.) 37
Миттаг-Леффлер (Mittag-Leffler, G.) 15 18 22 30 52 53 55
Неванлинна (Nevanlinna, R.) 73
Неограниченная логарифмическая диаграмма гл.1 § 5.3
Непосредственное аналитическое продолжение элементов гл.1 § 2.1
Нобль (Noble, M.E.) 70 71 74
Ньютон (Newton, I.) 5 14
Область эффективной суммируемости гл.1 § 6.1
Опорная функция гл.1 § 5.2
Особая точка (особенность) гл.1 §
Островский (Ostrowski, A.) 60
Относительная максимальная плотность гл.2 §
Относительная плотность гл.2 §
Относительно измеримое множество гл.2 §
Паде (Pade, H.) 16
Параметр лог-выпуклого множества гл.1 § 5.3
Переразложение степенного ряда гл.1 § 2.1
Пизо (Pisot, Ch.) 34
Пиранян (Piranian, G.) 70 82
Плотность гл.2 §
Полиа (Polya, G.) 21 33 47 61 63 64 67 72 77 82
Полная аналитическая функция гл.1 § 2.1
Полунепрерывные (матричные) методы гл.1 § 6.1
Полюсы (полярные особенности) гл.2 § 1.1
Преобразование Бореля гл.1 §
Приближения целыми функциями с касанием гл.1 § 3.3
Принсгейм (Pringsheim, A.) 60 61 66
Проблема эффективности аналитического продолжения гл.1 § 2.2
Пуанкаре (Poincare, H.) 11 12
Радиус мероморфности степенного ряда гл.2 § 1.1
Радиус сходимости степенного ряда гл.2 §
Рациональная функция гл.2 § 1.1; 5.5
Регулярная (голоморфная) функция гл.1 §
Регулярная (голоморфная) функция в точке гл.1 §
Регулярности дуга гл.1 §
Риман (Riemann, B.) 10 11 12 21
Риманова поверхность гл.1 §
Риччи (Ricci, G.) 70
Рунге (Runge, C.) 53
Спиральный угол гл.1 § 5.1
Степенной ряд гл.1 §
Тейлор (Taylor, B.) 47
Теорема Адамара о лакунах гл.2 § 1.2
Теорема Адамара об умножении особенностей гл.1 § 3.1
Теорема Фабри о лакунах гл.2 §
Теорема Фабри об отношении гл.2 §
Теорема Фабри общая гл.2 § 1.2;
Точка регулярности гл.1 §
Тригонометрическая выпуклость гл.1 § 5.2 5
Фабер (Faber, G.) 31 59 60 61 65 67 68 72
Фабри (Fabry, E.) 14 56 60 61 64 65 66 74 75 78 81 82
Формула Линделёфа гл.1 § 3.3
Фрагмен (Phragmen, E.) 25 32
Фрвдгольм (Fredholm, I.) 59
Харди (Hardy, G.) 72
Целая функция гл.1 §
Ширина компакта в направлении 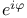 гл.1 § гл.1 §
Эгмон (Agmon, S.) 70
Эйзенштейн (Eisenstein, G.) 57 58
Эйлер (Suler, L.) 5 9 13 51
Экспоненциальный метод Бореля гл.1 § 6.1
Эрдёш (Erdoes, P.) 70 82
Эффективная матрица гл.1 § 6.1
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте