Let Ω be a domain with piecewise smooth boundary. In general, it is impossible to obtain a generalized solution u ∈ W 2 2 (Ω) of the equation
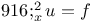
with the boundary conditions

by solving iteratively a system of two Poisson equations under homogeneous Dirichlet conditions. Such a system is obtained by setting v = −Δu. In the two-dimensional case, this fact is known as the Sapongyan paradox in the theory of simply supported polygonal plates. In the present paper, the three-dimensional problem is investigated for a domain with a smooth edge Γ. If the variable opening angle α ∈
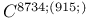
is less than π everywhere on the edge, then the boundary-value problem for the biharmonic equation is equivalent to the iterated Dirichlet problem, and its solution u inherits the positivity preserving property from these problems. In the case α ∈ (π, 2π), the procedure of solving the two Dirichlet problems must be modified by permitting infinite-dimensional kernel and co-kernel of the operators and determining the solution u ∈
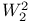
(Ω) by inverting a certain integral operator on the contour Γ. If α(s) ∈ (3π/2,2π) for a point s ∈ Γ, then there exists a nonnegative function f ∈

(Ω) for which the solution u changes sign inside the domain Ω. In the case of crack (α = 2π everywhere on Γ), one needs to introduce a special scale of weighted function spaces. In this case, the positivity preserving property fails. In some geometrical situations, the problems on well-posedness for the boundary-value problem for the biharmonic equation and the positivity property remain open.
 |
|
О проекте
|
|
О проекте


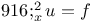 with the boundary conditions
with the boundary conditions  by solving iteratively a system of two Poisson equations under homogeneous Dirichlet conditions. Such a system is obtained by setting v = −Δu. In the two-dimensional case, this fact is known as the Sapongyan paradox in the theory of simply supported polygonal plates. In the present paper, the three-dimensional problem is investigated for a domain with a smooth edge Γ. If the variable opening angle α ∈
by solving iteratively a system of two Poisson equations under homogeneous Dirichlet conditions. Such a system is obtained by setting v = −Δu. In the two-dimensional case, this fact is known as the Sapongyan paradox in the theory of simply supported polygonal plates. In the present paper, the three-dimensional problem is investigated for a domain with a smooth edge Γ. If the variable opening angle α ∈ 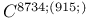 is less than π everywhere on the edge, then the boundary-value problem for the biharmonic equation is equivalent to the iterated Dirichlet problem, and its solution u inherits the positivity preserving property from these problems. In the case α ∈ (π, 2π), the procedure of solving the two Dirichlet problems must be modified by permitting infinite-dimensional kernel and co-kernel of the operators and determining the solution u ∈
is less than π everywhere on the edge, then the boundary-value problem for the biharmonic equation is equivalent to the iterated Dirichlet problem, and its solution u inherits the positivity preserving property from these problems. In the case α ∈ (π, 2π), the procedure of solving the two Dirichlet problems must be modified by permitting infinite-dimensional kernel and co-kernel of the operators and determining the solution u ∈ 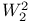 (Ω) by inverting a certain integral operator on the contour Γ. If α(s) ∈ (3π/2,2π) for a point s ∈ Γ, then there exists a nonnegative function f ∈
(Ω) by inverting a certain integral operator on the contour Γ. If α(s) ∈ (3π/2,2π) for a point s ∈ Γ, then there exists a nonnegative function f ∈  (Ω) for which the solution u changes sign inside the domain Ω. In the case of crack (α = 2π everywhere on Γ), one needs to introduce a special scale of weighted function spaces. In this case, the positivity preserving property fails. In some geometrical situations, the problems on well-posedness for the boundary-value problem for the biharmonic equation and the positivity property remain open.
(Ω) for which the solution u changes sign inside the domain Ω. In the case of crack (α = 2π everywhere on Γ), one needs to introduce a special scale of weighted function spaces. In this case, the positivity preserving property fails. In some geometrical situations, the problems on well-posedness for the boundary-value problem for the biharmonic equation and the positivity property remain open.