A triangulation of a manifold (or pseudomanifold) is called a tight triangulation if any simplexwise linear embedding into any Euclidean space is tight. Tightness of an embedding means that the inclusion of any sublevel selected by a linear functional is injective in homology and, therefore, topologically essential. Tightness is a generalization of convexity, and the tightness of a triangulation is a fairly restrictive property. We give a review on all known examples of tight triangulations and formulate a (computer-aided) enumeration theorem for the case of at most 15 vertices and the presence of a vertex-transitive automorphism group. Altogether, six new examples of tight triangulations are presented, a vertex-transitive triangulation of the simply connected homogeneous 5-manifold SU(3)/SO(3) with vertex-transitive action, two non-symmetric 12-vertex triangulations of

, and two non-symmetric triangulations of
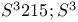
on 13 vertices.
 |
|
О проекте
|
|
О проекте


 , and two non-symmetric triangulations of
, and two non-symmetric triangulations of 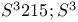 on 13 vertices.
on 13 vertices.