Пусть

– независимые одинаково распределенные случайные величины с функцией распределения

,

Получены близкие к правильным оценки сверху и снизу для

,

при
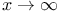
,

, а также оценки для

, где

при подходящих функциях
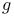
. Относительно распределения
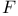
предполагается, что “хвосты”

и

,
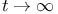
, мажорируются или минорируются правильно меняющимися функциями либо вида

, где

– медленно меняющаяся функция, либо вида

,

. В качестве следствий установлены относительная равномерная сходимость распределений сумм к устойчивому закону и закон повторного логарифма для последовательности

в случае

.
 |
|
О проекте
|
|
О проекте


 – независимые одинаково распределенные случайные величины с функцией распределения
– независимые одинаково распределенные случайные величины с функцией распределения  ,
,

 ,
,  при
при 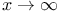 ,
,  , а также оценки для
, а также оценки для  , где
, где

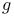 . Относительно распределения
. Относительно распределения 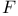 предполагается, что “хвосты”
предполагается, что “хвосты”  и
и  ,
, 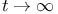 , мажорируются или минорируются правильно меняющимися функциями либо вида
, мажорируются или минорируются правильно меняющимися функциями либо вида  , где
, где  – медленно меняющаяся функция, либо вида
– медленно меняющаяся функция, либо вида  ,
,  . В качестве следствий установлены относительная равномерная сходимость распределений сумм к устойчивому закону и закон повторного логарифма для последовательности
. В качестве следствий установлены относительная равномерная сходимость распределений сумм к устойчивому закону и закон повторного логарифма для последовательности  в случае
в случае  .
.