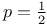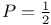Книга профессора Колорадского университета (США) Дж. Тейлора является пособием по математической обработке результатов измерений в учебных физических лабораториях. Подробно разъясняются неизбежность ошибок измерений, способы фиксирования результатов измерений и на основе нормального распределения рассматриваются элементы статистической обработки случайных ошибок, обсуждаются проблема «промахов», «взвешивание» результатов различных измерений, метод наименьших квадратов, корреляции, распределение Пуассона и биномиальное распределение, критерий
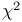
. В конце каждой главы приведены задачи, для большинства которых в конце книги имеются ответы и решения. Для студентов и преподавателей вузов, сотрудников измерительных лабораторий, а также учащихся средних специальных учебных заведений и старшеклассников.
 |
|
О проекте
|
|
О проекте


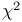 . В конце каждой главы приведены задачи, для большинства которых в конце книги имеются ответы и решения. Для студентов и преподавателей вузов, сотрудников измерительных лабораторий, а также учащихся средних специальных учебных заведений и старшеклассников.
. В конце каждой главы приведены задачи, для большинства которых в конце книги имеются ответы и решения. Для студентов и преподавателей вузов, сотрудников измерительных лабораторий, а также учащихся средних специальных учебных заведений и старшеклассников.