|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Swinnerton-Dyer H.P.F. — A brief guide to algebraic number theory |
|
|
 |
| Предметный указатель |
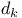 4 4
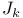 15 50 15 50
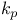 34 34
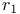 , , 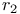 3 3
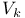 49 49
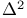 4 4
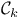 15 15
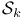 16 16
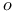 , , 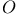 1 1
 53 53
Absolute norm 13
Absolute value 31
Adele 48
Adele, principal 49
Algebraic number field vii
Approximation, strong 40
Approximation, weak 39
Archimedean 32
Artin element, symbol 29
Artin map 100
Artin map, local 108
Artin reciprocity law 100
Ascending chain condition 6
Cebotarev density theorem 96
CHARACTER 125
Character, congruence 79
Character, Hecke Groessencharakter 82 90 104
Character, Tate 84
Characteristic polynomial 121
Chinese remainder theorem 12
Circle group 125
Class field 99
Class field theory viii
Class number 15
Conductor 43 68 99 100
Congruence divisor class group 99
Conorm 23
Cyclotomic 65
Dedekind domain 9
density 94
Density, Dirichlet 94
Diagonal map 49 51
Different 43 44
Different, local 44
Discriminant, absolute 4
Discriminant, relative 26
Exercise 17 19 40 43 62 69 76 111
Fermat's last theorem vii 73
First degree primes 94
Frobenius element 29 134
Gauss sum 69
H 15
Haar measure, integral 123
Hasse norm theorem 102
| Height 16
Hensel's lemma 35
Hilbert basis theorem 8
Hilbert symbol 107 108
Hilbert's theorem 90 4
Ideal class group 15
Ideal, fractional 10
Ideal, integral 10
Idele 48 50
Idele class group 105
Idele, principal 51
Inertia group, field 28
Integer, algebraic 1146
Integral at p 14
Integral closure 3
Kronecker — Weber Theorem viii 112
L-series, Dirichlet 79
Lattice 120
Local field 35
Minimal base 118
Noetherian 6
Norm 121
Order 3
Pigeonhole Principle 16 120
Place 31
Place, finite 34
Place, infinite 33
Pontryagin duality 125
Power residue symbol 106
Product formula 35 50
Quadratic reciprocity law 61
Quasi-character 128
R 23
Ramification 41
Ramification group 28
Ramification, tame 41
Ramification, wild 41
Ramified primes 15
Reduced form 57
Regulator 23
Riemann hypothesis 79
Splitting group, field 27
Stickelberger 5
t 125
Trace 121
Transform, Fourier 128
Transform, Mellin 130
Ultrametric 34
UNIT 15
Unit, cyclotomic 71
Unit, fundamental 58
Valuation, additive 35
Valuation, multiplicative 31
Zeta function, Riemann 79
Zeta function, Tate 84
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



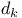
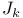
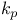
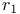 ,
, 
 ,
,