|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hardy G.H., Wright E.M. — An Introduction to the Theory of Numbers |
|
|
 |
| Предметный указатель |
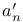 133 139 133 139
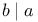 , , 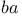 1 1
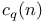 55 55
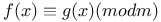 82 82
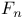 (Fermat number) 14 (Fermat number) 14
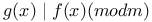 83 83
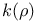 179 179
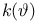 204 204
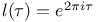 54 54
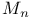 (Mersenne number) 16 (Mersenne number) 16
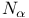 (norm) 182 187 208 (norm) 182 187 208
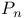 6 6
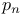 , , 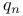 (convergents) 130 (convergents) 130
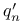 137 140 137 140
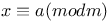 , , 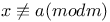 49 49
![$[x]$](/math_tex/7e1c4a3a07c941625c2f20c594cb9f7c82.gif) 74 74
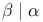 , , 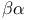 , , 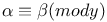 (in k(i) and other fields) 182 188 208 219 (in k(i) and other fields) 182 188 208 219
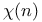 240 240
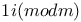 , , 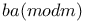 89 89
 (unity) 181 182 208 (unity) 181 182 208
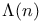 253 253
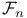 (Farey series) 23 (Farey series) 23
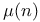 234 234
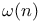 , , 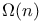 354 354
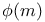 52 52
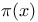 6 6
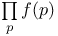 , , 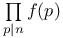 48 48
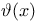 , , 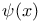 340 340
 245 245
(a,b), (a,b,...,k) 20
(x), 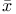 156 156
a belongs to d (mod m) 71
Ahrens 128
Algebraic field 204
Almost all (integers) 8
Almost all (real numbers) 122
Anderson 243
Apostol 243
aRp, aNp, 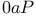 67—68 67—68
Asymptotically equivalent, asymptotic to 8
Atkin 289 295
Atkinson 272
Austin 22
Bachet 115—117 202 315
Bachmann 81 106 153 189 202 216 243 272 295 388
Baer 335
Ball, Rouse 2 2
Bang 373
Bastion 338
Bateman 2 2
Bauer 98 99 101 103 104 106
Beeger 81
Berg 217
Bernes 217
bernoulli 90 91 202 245
Bernstein 168 177
Bertrand 343 373
Binet 199
Bocher 397
Bochner 189 232
Bohl 393
Bohr 22 259 388 393
Borel 128 168 177
Boulyguine 316
Brilka 128
Bromwich 259
Brun 296
Cantor 124 160 176
Carmichael 11
Cassels 128 412 413
Cauchy 36 168
Champernowne 128
Chatland 217
Chen 337
Cherves 153
Cherwell 272 374 F.
Chowla 106
Chrystal 153
Cipolla 81
Clausen 93
Copeland 128
Coprime 48
Coxeter 22
d(n), 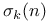 , ,  238 238
Darling 295
Darlington 106
Davenport vii 22 217 335 336 411—413
de la Vallee-Poussin 11 374
de Polignac 373
Dedekind 377
Democritus 42
Dickson vii 11 22 36 80 81 106 128 153 201—203 217 243 295 315 316 335 337—339 373 412
Diophantus 201 202
Dirichlet 13 18 62 93 113 156 157 169 176 244 245 248 251 257 259 272 375
Duparc 81
Durfee 281
Dyson 176 177 289 295 296 413
Eisenstein 62 106 189
Enneper 296
Eratosthenes 3
Erchinger 62
Erdos 22 128 373 374
Errera 374
Escott 338
Estermann 22 316 336 386 393
Euclid 3 4 10—14 16 18 21 40 43 44 58 134 136 159 176 179—182 185 187 212—217 225 230—232 239 240 307 340
Euclidean construction 159
Euclidean field 212
Euclidean number 159
Eudoxus 40
Euler 14 16 22 39 52 62 63 65 80 81 90 163 199 201—203 219 243 246 259 264 274 277 280 284 285 287 289 295 315 332 338 347 351 373
Farey 23 29 30 36 37 268
Fauquembergue 339
Fermat 6 14 15 18 19 58 71—73 78; 81 85—87 105 202 219 222 231 299 300 332 338
Ferrar 397
Ferrier 16 22
fibonacci 148 150 153 223
Fine 295
Fleck 338
Franklin 286 295
g(k), G(k) 298
Gauss 10 14 39 47 54 58 62 63 73—76 81 106 178 179 182 185 189 243 272 295 303 316 400 412
Gegenbauer 272
Gelfond 47 176 177
Gerardin 203 339
Gillies 22
Gleisher 106 316 373
Gloden 338
Goldbach 19 22
Goldberg 81
Grace 301 315
Grandjot 62
Gronwall 272
Grunert 128
Gupta 289 295
Gwyther 295
hadamard 11 374
Hajos 37 412
Hall 373
Hardy 106 159 168 259 272 289 296 316 335 336 338 374
Haros 36
Hasse 22
Hausdorff 128
Heaslet 316
Heath 42 43 47 201
Hecke 22 93 159
Heilbronn vii 212 213 217 336 413
hermite 47 177 315 412
Highest common divisor 20
hilbert 177 298 315 335 336
| Hlawka 413
Hobson 128 176
Holder 243
Hua 336
Hunter 338
Hurwitz, Adolf 37 81 177 203 315 316 338 412
Hurwitz, Alexander 16 22
Ingham 11 22 232 259 373
jacobi 189 243 259 282 283 285 289 295 315 316
Jacobstal 106
James 22 335 336
Jensen 62
Jessen 393
k(1) 178
k(i) 179
Kalmar 373
Kanold 243
Kempner 335 338
Khintchine 177
Kiihnel 243
Kloosterman 56 62
Koksma 128 177 393 411 412
Kolberg 295
Konig 128 378 393
Korkine 412
Kraitchik 11 22
Krecmar 289 295
kronecker 62 375—378 382—384 386 388 390 392 393
Kulik 11
Kummer 202
Lagrange 87 93 98 153 197 302 315
Lambert 47 257
Landau vii 11 22 37 62 81 177 201 202 232 243 259 272 316 335 336 373 374 412 413
Lander 339
Landry 15
Least common multiple 48
Lebesgue 128
Leech 203 339 374
legendre 63 68 80 81 202 315 316 320
Lehmer, D. H. 11 16 22 81 148 153 202 213 217 231 289 295 374
Lehmer, D. N 10 11 373
Lehmer, E. 202 374
Lehner 289 295
Leibniz 81
Letac 338
Lettenmeyer 384 386 393
Leudesdorf 101 106
Lindemann, F. 177
Lindemann, F. A. 22 (see also “Cherwell”)
Linear independence of numbers 379
Linfoot 213 217
Linnik 335
Liouville 161 176 316 338
Lipschitz 316
Littlewood 11 22 335 336 338 374 393
Lucas 11 16 22 81 148 223 225 231 232
Macbeath 412
Maclaurin 90
MacMahon 278 286 287 289 295
Mahler 339 413
Maillet 338
Mapes 11
Markoff 412
Mathews 62
mersenne 14—16 18 80 148 223 224 240
Mertens 272 351 373
Miller 16 22 81 295
Mills 373
Milne v
min(x,y), max(x,y) 48
Minimal residue (mod m) 73
Minkowski 23 31 32 33 37 394 402 407 411—413
mobius 234 236 243 251 252 360
Moessner 339
Mordell 33 37 202 203 295 316 327 338 339 394 412 413
Morehead 15
Morse 243
Moser 373
Multiplicative function 53
Napier 8
Netto 295
Nevanlinna 374
Newman 231 287 295
Newton 328
Nicol 202
Niven 47 128 337
Nogues 202
Norrie 339
O, o,  , , 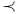 , , 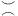 , , 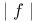 , A (unspecified constant)) 7 , A (unspecified constant)) 7
Of the same order of magnitude 7
Oppenheim 2 17
P(k,j) 328—329
p(n) 273
Palama 338
Parkin 339
Patterson 339
Pearson 81
Pell 217
Perron vii 153 177
Pervusin 16
Pillai 337
Plato 42 43
Polya 14 22 37 128 243 259 272 374
Ponting v
Potter vii.
Primitive root of m 71
Primitive root of unity 55
Prouhet 328 338
Pythagoras 39 40 42 43 47 201
Quadratfrei 16
r(n), 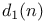 , , 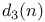 240—241 240—241
Rademacher 47 289
Rado vii 93 412
Rama Rao 93 106
Ramanujan 55 56 62 201 237 243 256 259 265 272 287 289 290 291 295 296 316 373
Reid 217
Remak 413
Richmond 62 202 327 338
Riemann 245 259
Riesel 16 22
Riesz 259
Robinson 16 22 81
Rogers 290 291 296 413
rosser 202
Roth 176
Rubugunday 337
Ryley 202
Saltoun 315
Sastry 339
Schmidt 413
Schneider 177
schur 291 296 338
Seelhoff 16
Segre 203
Selberg, A. 296 359 360 373 374
Selberg, S. 374
Selfridge 16 22 81 202
Shah 374
Siegel 176 411 412
Sierpinski 393
Simple field 212
Skolem 295
smith 316
Sommer 216
Staeckel 374
Standard form of n 2
Stark 213 217
Stemmler 337
Subba Rao 339
Sudler 296
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



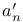
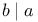 ,
, 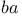
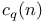
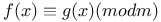
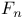 (Fermat number)
(Fermat number) 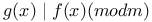
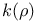
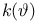
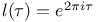
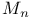 (Mersenne number)
(Mersenne number) 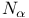 (norm)
(norm) 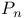
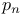 ,
, 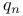 (convergents)
(convergents) 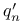
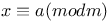 ,
, 
![$[x]$](/math_tex/7e1c4a3a07c941625c2f20c594cb9f7c82.gif)
 ,
,  ,
, 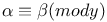 (in k(i) and other fields)
(in k(i) and other fields) 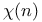
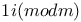 ,
, 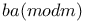
 (unity)
(unity) 
 (Farey series)
(Farey series) 
 ,
, 
 ,
, 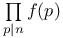
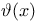 ,
, 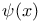

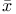
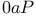
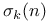 ,
, 
 ,
, 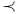 ,
, 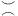 ,
, 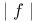 , A (unspecified constant))
, A (unspecified constant)) 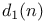 ,
,