|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Soong T.T. — Fundamentals of probability and statistics for engineers |
|
|
 |
| Предметный указатель |
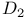 distribution 327 distribution 327
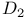 distribution, table 372 distribution, table 372
Average value see “Mean”
Axioms of probability 13—14
Bayes's theorem 24—25
Bernoulli trials 161
Beta distribution 221—226 237
Beta distribution, generalized 225—226
Beta distribution, mean 223 237
Beta distribution, variance 223 237
Bias 265
Binomial distribution 43 162 182—183
Binomial distribution, characteristic function 164
Binomial distribution, mean 164 184
Binomial distribution, Poisson approximation 182—183
Binomial distribution, table 365—366
Binomial distribution, variance 164 184
Boole's inequality 30
Brownian motion 106
Cauchy distribution 126
Central limit theorem 199—201
Characteristic function 98
Characteristic function, joint 108
Chebyshev inequality 86—87
Chi-squared distribution 219—221 236
Chi-squared distribution, mean 221 236
Chi-squared distribution, table 371
Chi-squared distribution, variance 221 236
Chi-squared text 316
Coefficient of excess 83
Coefficient of skewness 83
Coefficient of variation 81
Computer software 3 375—377
Confidence interval 295 296 298 302
Confidence limit 347
Consistency 274
Correlation 88—90
Correlation coefficient 88—89
Correlation, perfect 90
Correlation, zero 90
Covariance 88
Covariance, matrix 93
Cramer — Rao inequality 267—270
Cramer — Rao inequality, lower bound (CRLB) 269
Cumulant 101
Cumulative distribution function see “Probability distribution function”
De Morgan's laws 11—12
Density function see “Probability density function”
Distribution function see “Probability distribution function”
Efficiency 270
Efficiency, asymptotic 271
Error 316
Error, type I 316
Error, type II 316
Estimate 264
Estimator 265
Estimator, consistent 274
Estimator, efficient 270 271
Estimator, sufficient 275
Estimator, unbiased minimum-variance 266
Event 12
Excel 2000 3
Expectation 75—76
Expectation, conditional 83—85
Expectation, mathematical 75
Expectation, operator 75
Exponential distribution 45 78 215—219 236
Exponential distribution, mean 215 236
Exponential distribution, variance 215 236
Exponential failure law 218
Extreme-value distribution 226
Extreme-value distribution, type I 228 237
Extreme-value distribution, type II 233 237
Extreme-value distribution, type III 234 237
Failure rate see Hazard function
Fisher — Neyman factorization criterion 275
Frequency diagram 248
Function of random variables 119 137
Function of random variables, moments 134
Function of random variables, probability distributions 120
Gamma distribution 212—215 236
Gamma distribution, mean 213 236
Gamma distribution, variance 213 236
Gauss — Markov theorem 345
Gaussian distribution see Normal distribution
Geometric distribution 167 184
Geometric distribution, mean 168 184
Geometric distribution, variance 168 184
Gumbel's extreme value 228
Gumbel's extreme value, distribution 228
Hazard function 218
histogram 248
Histogram, cumulative 327
Hypergeometric distribution 167 184
Hypergeometric distribution, mean 184
Hypergeometric distribution, variance 184
Hypothesis testing see “Test of hypothesis”
Independence 19—20
Independence, mutual 18
Interarrival time 215
Jacobian 149
Kolmogorov — Smirnov test 327
Law of Large Numbers 96
Least-square estimator 354—355
Least-square estimator, covariance 356
Least-square estimator, linear unbiased minimum variance 344
Least-square estimator, mean 355
Least-square estimator, variance 355
Likelihood equation 288
Likelihood function 288
Linear regression 335
Linear regression, multiple 354
Linear regression, other models 357
Linear regression, simple 335
Linear regression, variance 343
Lognormal distribution 209—212 236
Lognormal distribution, mean 211 236
Lognormal distribution, variance 211 236
Maclaurin series 99
Markov's inequality 115
Markovian property 27
Mass function see “Probability mass function”
Maximum likelihood estimate 288
Maximum likelihood estimator 288—289
Maximum likelihood estimator, consistency 289
Maximum likelihood estimator, efficiency 289
Maximum likelihood estimator, invariance property 290
Mean 76—77
| Mean, conditional 84
Median 76
MODE 78
moment 76 78
Moment estimate 278
Moment estimator (ME) 278—280
Moment estimator (ME), combined 284
Moment estimator (ME), consistency 279
Moment, central 79
Moment, joint 87
Moment, joint central 87
Moment-generating function 112 117
Multinomial distribution 172 184
Multinomial distribution, covariance 173
Multinomial distribution, mean 173 184
Multinomial distribution, variance 173 184
Mutual exclusiveness 13
Negative binomial distribution 169 184
Negative binomial distribution, mean 171 184
Negative binomial distribution, variance 171 184
Normal distribution 107 196—199 236
Normal distribution, bivariate 111
Normal distribution, characteristic function 198
Normal distribution, mean 198 236
Normal distribution, multivariate 205
Normal distribution, standardized 201
Normal distribution, table 369
Normal distribution, variance 198 236
Normal equation 338
Nuisance parameter 284
Parameter estimation 259
Parameter estimation, interval estimation 294—295
Parameter estimation, maximum likelihood method 287
Parameter estimation, moment method 278
Parameter estimation, point estimation 277
Pascal distribution see “Negative binomial distribution”
Poisson distribution 173—176 184
Poisson distribution, mean 176 184
Poisson distribution, table 367
Poisson distribution, variance 176 184
Population 259
probability 13
Probability density function (pdf) 44—46
Probability density function (pdf), conditional 62—63
Probability density function (pdf), joint (jpdf) 49—51
Probability density function (pdf), marginal 57
Probability distribution function (PDF) 39—41
Probability distribution function (PDF), bivariate 49
Probability distribution function (PDF), conditional 61
Probability distribution function (PDF), joint (JPDF) 49—51
Probability distribution function (PDF), marginal 50
Probability distribution function (PDF), mixed-type 46
Probability mass function (pmf) 41 43
Probability mass function (pmf), conditional 61
Probability mass function (pmf), joint (jpmf) 51—55
Probability mass function (pmf), marginal 52
Probability, assignment 16 17
Probability, conditional 20—21
Probability, function 13
Probability, measure 13
Random experiment 12
Random sample see “Sample”
Random variable 37—39
Random variable, continuous 38
Random variable, discrete 38
Random variable, function of 120
Random variable, sum of 145
Random vector 39
Random walk 52
Range space 120
Regression coefficient 336
Regression coefficient, confidence interval 347
Regression coefficient, least-square estimate 344
Regression coefficient, test of hypothesis 316
Relative likelihood 16—17
Reliability 60 218
Residual 337
Return period 169
Sample 259
Sample moment 263—264
Sample point 12
Sample space 12
Sample variance 262—263
Sample variance, mean 262
Sample variance, variance 262
Sample, mean 97 261
Sample, size 260
Sample, value 260
Sample, variance 261
Schwarz inequality 92
Set 8—12
Set operation 9—12
Set operation, difference 10
Set operation, intersection (product) 10
Set operation, union (sum) 9
Set, complement of 9
Set, countable (enumerable) 8
Set, disjoint 10
Set, element 8
Set, empty 9
Set, finite 8
Set, infinite 8
Set, subset of 8
Set, uncountable (nonenumerable) 8
Significance level 319
Spreadsheet 3
Standard deviation 79—81
Statistic 260
Statistic, sufficient 275
Statistical independence see “Independence”
Sterling's formula 107
Student's t-distribution 298—299
Student's t-distribution, table 370
Sum of random variables 93 145—146
Sum of random variables, characteristic function 104—105
Sum of random variables, moment 94
Sum of random variables, probability distribution 106 146
Test of hypothesis 316
Total probability theorem 23
Tree diagram 27—28
Unbiasedness 265
Uniform distribution 57 189 236
Uniform distribution, bivariate 193
Uniform distribution, mean 192 236
Uniform distribution, variance 192 236
Unimodal distribution 79
Unimodal distribution, variance 79 82
Venn diagram 9
Weibull distribution 235
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



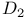 distribution
distribution