|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Eisenbud D., Harris J. — The Geometry of Schemes |
|
|
 |
| Предметный указатель |
Singularity, 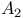 204 204
Small resolutions 179
Smith, Gregory 5
Smooth point 230
Smoothness 71
Spanier, Edwin H. 261
Spectrum 9
Spectrum of Noetherian ring 26
Spectrum of quotient ring 23
Spectrum of R-algebra 40
Stalk 13
Starr, Jason 5
Strict transform 168
Structure sheaf 9 11 19
Subfunctor 254
Subfunctor, closed 255
Subfunctor, open 254
Subscheme, Cartier 165 167 168 175 176 178 182
Subscheme, closed 23 24 71 211
Subscheme, degree of 125
Subscheme, diagonal 93
Subscheme, locally closed 26
Subscheme, open 23
Subscheme, regular 165 172
Subsheaf 16
Support 21 58 220
Support of a sheaf 220
Swan, Richard G. 18
Sylvester, determinant 224 235
Sylvester, matrix 226
Symmetric algebra 102 105 122 173
Syzygy 79
Syzygy, theorem 128
Tacnode 156 239
Tangent cone 106—110 171 178 190 192 203 204
Tangent cone, projectivized 107
Tangent developable 109
Tangent projective 152
Tangent space to Fano schemes 271
Tangent space to Hilbert schemes 267
Tangent space, affine 104 105
Tangent space, projective 104 105
Tangent space, Zariski 73 78 88 104 107 108 256 260 271
| Tautological family 276
Tautological sheaf 119
Terminal object 31
Total transform 168
transform 168
Twist 119
Union of schemes 24
Universal bundle 206
Universal conic 207 208
Universal cubic 203 204
Universal curve 155
Universal family 123 222 263 276
Universal family of pairs of polynomials 226
Universal Fano scheme 203
Universal Fano variety 204
Universal formula 213
Universal hyperplane 124
Universal hypersurface 123
Universal line 240
Universal line section 240
Universal morphism 165
Universal property of blow-up 168
Universal quadric 202
Universally closed 95
Upper-semicontinuous 73
Vakil, Ravi 5
Vanishes on subscheme 25
Variety see “Scheme classical
Veronese, map 101 109
Veronese, subring 100
Veronese, subsheaf 102
Vistoli, Angelo 277
Vogel, Wolfgang 148
Walker, Robert J. 52
Wedderburn theorems 206
Weil, conjectures 1
Yoneda’s Lemma 251 252 258 263
Zariski, cotangent space 27
Zariski, Oskar 27 28
Zariski, tangent space 27 28 73 78 88 104 105 107 108 256 260 271
Zariski, topology 9—11 48 70 93 130 230 259—261
Zariski, topology, base for 11
Zero-dimensional scheme 27 28 64—66 72
“Little Gidding” v
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте