|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Molchanov I.I. — Limit theorems for unions of random closed sets |
|
|
 |
| Предметный указатель |
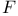 -addition 23 -addition 23
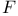 -closed set 20 -closed set 20
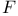 -expectation of a random set 19 -expectation of a random set 19
 -convergence 2 -convergence 2
Addition-scheme 15
Alternating Choquet capacity 3
Alternating Choquet capacity of in nite order 30
Ambarzumian, R.V. 147
Approximation of convex sets 38 139
Araujo, A. 17 147
Arrow, K.J. 17 147
Artstein, Z. 15 16 85 147
Asymptotic inverse function 13 56
Attouch, H. 134 147
Aubin, J.-P. 85 147
Aumann, R. 15 147
Baddeley, A.J. 103 112 147
Balkema, A.A. 30 41 147
Ball 1
Berg, C. 30 147
Bhattacharia, R.N. 26 147
Billingsley, P. 10 147
Boolean model 35
Boolean model as U-stable set 36
Boolean model, simulation 123
Borel — Cantelli lemma 72
Boundary of a set 2
C-stable random set see Convex-stable random set
Canonically closed set 2
Capacity functional 3
Capacity integral 18
Capacity, homogeneous 30 45 109
Capacity, maxitive see Maxitive capacity
Capacity, regularly varying 69
Castaign representation 102
Cauchy distribution 60 119
Central limit theorem for random sets 17
Choquet capacity 3
Choquet theorem 3
Choquet, G. 6 36 147
Christensen, J.P.R. 30 147
Clarke, H. 85 147
Closure of a set 2
Compacti cation 5
Complement 2
Cone 59
Cone, canonically closed 86
Continuity set 7
Convergence of capacities, pointwise 48 49
Convergence of capacities, uniform 49
Convergence of closed sets 1
Convergence of compact sets 2
Convex hull 2
Convex random set 5
Convex-stable random set 38
Convex-stable random set of the first type 41
Convex-stable random set of the second type 41
Corrosion propagation 129
Cressie, N.A.C. 1 17 147
Davis, R.A. 38 67 68 71 74—76 79 82 127 148
Density regularly varying 55
Disease propagation 127
Dudley, R.M. 27 148
Ekeland, I. 85 147
Engineering metric 102
Envelope of a set 2
Epi-convergence 140
Epigraph 139
Equilibrium measure 37
Euclidean metric 1
Euclidean norm 1
Euclidean space 1
Expectation of a random set 11 15
Exponent of a regularly varying function 13
Exponent of a regularly varying function, multivariate 14
Feller, W. 13 148
Fixed point 29
Frankowska, H. 85 147
Function, asymptotic inverse 13
Function, multivalued 86
Function, regularly varying 46
Function, upper semi-continuous 134
Functional, homogeneous 111
Functional, strictly monotone 70
Galambos, J. 30 38 41 45 49 50 53 148
Gaussian random sample 130
Gaussian random set 17
Gerritse B. 18 148
Gerritse, G. 65 148
Gine, E. 15 17 18 30 38 40 41 147 148
Groeneboom, P. 139 148
Haan, L. de 13 14 30 77 95 148
Hahn, F.H. 17 147
Hahn, M. 15 17 18 38 148
Hausdor metric 2
Hengartner, W. 106 108 148
Hiai, F. 15 85 148 149
Hitting functional 3
Homogeneous capacity 30 45 109
Homogeneous function 14
Homogeneous metric 102 110
Huber, P. 18 149
Hypo-convergence 134
Hypograph 134
Ideal metric 110
Inclusion functional 6 38 51
Index of a regularly varying function 13
Index of a regularly varying function, multivalued 86
Index of a regularly varying function, multivariate 14
Intensity measure 35
Interior of a set 2
Inverse function 91
Inversion of a set 34
Ito, K. 149
K-convergence 2
Kalashnikov, V.V. 101 149
Kendall, D.G. 1 3 149 151
Kernel 36
Khinchin lemma 43 44 65
Kruse, R. 16 149
Landkof, N.C. 36 37 111 149
Laslett, G.M. 1 147
Law of large numbers for Minkowski sums 16
Law of large numbers for unions 71
Leadbetter, M.R. 30 43 149
Lebesgue measure 11 16
Lebesgue measure on the sphere 58
Levy metric for random sets 103
Levy metric for random variables 107
Levy — Prokhorov metric 101
| Lindgren, G. 149
Lyashenko, N.N. 4 7 8 17 138 149
Markov inequality 130
Matheron, G. 1 3 12 18—20 22 29—31 35 37 57 67 69 73 108 111 123 132 149
Max-stable distribution 30
Max-stable random process 30
Max-stable random variable 30
Max-stable random vector 30 41
Maximum principle 36
Maxitive capacity 4 36
McClure, D.E. 139 149
McKean, H.P. 149
Mecke, J. 1 151
Minitive capacity 70
Minkowski addition 2 12
Minkowski functionals 108
Minkowski subtraction 12
Molchanov, I.S. 4 5 8 16 26 27 31 71 85 134 149 150
Monotone capacity of infinite order 6
Mulrow, E. 67 127 148
Multivalued function 85
Multivalued function, convex-valued 88
Multivalued function, homogeneous 115
Multivalued function, regularly varying 86
Multivariate regularly varying function 14
Newton capacity 111
Norberg, T. 1 4 8 18 30 65 70 99 134 135 138 150
Norm of a set 12 15
Omey, E. 14 148
Outer normal vector 139
Pancheva, E. 65 150
Papageorgiou, N.S. 85 150
Poisson point process 35 57
Poisson point process, stationary 35
Polygonal approximation 139
Polyhedron random 139
Probability metric 101
Probability metric, homogeneous 102 110
Probability metric, ideal 110
Probability metric, regular 110
Probability metric, semi-homogeneous 118
Probability metrics method 101
Puri, M.L. 15 150
Rachev, S.T. 101 103 149 150
Ralescu, D.A. 15 150
Random ball 84 85
Random closed set 2
Random closed set, additive U-stable 43
Random closed set, compact 5
Random closed set, convex 5
Random closed set, convex-stable 38
Random closed set, generalized U-stable 42
Random closed set, homogeneous at infinity 43
Random closed set, inverted U-stable 44
Random closed set, isotropic 5
Random closed set, non-trivial 29
Random closed set, simulation 124
Random closed set, stationary 5
Random closed set, strictly C-stable 38
Random closed set, U-stable 30
Random closed set, union stable 30
Random closed set, union-in nitely-divisible 29
Random constraints 144
Random half-space 142
Random sample 67
Random set, Gaussian 17
Random set, p-stable 18
Random triangle 125
Random variable max-stable 30
Random vector max-stable 30 41
Ranga Rao, R. 26 147
Regular metric 110
Regularly varying function 13
Regularly varying function at zero 49
Regularly varying function index 13
Resnick, S.I. 14 30 41 67 74 76 77 95 127 147 148 150
Ressel, P. 30 147
Riesz capacity 37
Robbins formula 123 132
Robbins, H.E. 123 150
Rockafellar, R.T. 85 91 150
Rootzen, H. 149
Rose of directions 128
Salinetti, G. 4 7 8 85 134 135 140 150 151
Santalo, L.A. 131 151
Schneider, R. 38 129 139 151
Selector 22 102
Semi-homogeneous metric 117
Seneta, E. 13 46 56 69 89 151
Serra, J. 12 123 151
Set-valued function 85
Shapley — Folkmann lemma 17
Space of closed sets 1
Stable random process 37
Standard class 105
Star-cluster 38 127
Steiner formula 108
Stoyan, D. 1 11 12 16 18 20 24 35 108 123 151
Stoyan, H. 16 18 151
Support function 7 12
Theodorescu, R. 106 108 148
Tomkins, R. 74 76 150
Total variation distance 108
Trader, D.A. 5 29 40 43 151
Umegaki, H. 85 149
Uniform for random variables 103
Uniform metric for random sets 103
union 11
Union-scheme 45
Union-stable random set 30 109
Union-stable random set, simulation 124
Unit sphere 9
Upper limit in  2 2
Upper limit in  2 2
Upper semi-continuous function 5
Upper semi-continuous functional 3
Uryson, P.S. 131 151
Variance of a random set 16
Vatan, P. 38 148
Vervaat, W. 1 150 151
Vitale, R.A. 5 11 15—18 22 57 130 139 147 149 151
Volume of random samples 129
Wagner, D. 151
Weak convergence of random sets 7 104
Weak convergence, determine class 8
Weak convergence, determining class 104
Weil, W. 17 26 151
Wets, R.J.-B. 4 7 8 85 91 134 135 140 147 151
Yakimiv, A.L. 14 77 86 87 151
Zinn, J. 148
Zolotarev, V.M. 65 101—103 108 110 114 151 152
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



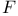 -addition
-addition  -convergence
-convergence 