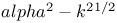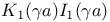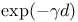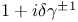|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Нобл Б. — Метод Винера-Хопфа для решения дифференциальных уравнений в частных производных |
|
|
 |
| Предметный указатель |
Абелевы теоремы 48 59 70
Алблас 112 263
Амен 59
Аналитическое продолжение 17 50
Антенна биконическая 246
Антенна цилиндрический стержень 240
Асимптотические разложения в приближенных решениях 225 (см. также «Поле в дальней зоне»)
Асимптотические разложения контурных интегралов 45 58
Асимптотические разложения преобразований 48
Базер 88 148 173 190
Бай Ши-и 160
Баукамп 90 203 246
Бейкер 84 233
Бейлин 141
Берз 153
Бесконечное произведение 26 52 119 149 150
Бесконечное произведение для гамма-функции 53
Бесконечное произведение, асимптотическое поведение 120 147 148
Бесконечное произведение, вычисление 146 147
Бигармоническое уравнение напряжения в полосе 159 (см. также «Упругая среда»)
Бигармоническое уравнение приближенная факторизация 185
Болдуин 144
Бреммер 38 48
Вайнштейн, Л.А. 31 133 144 150 152 175
Вайнштейна — Карпа — Клеммова метод 62 175 240
Ван дер Поль 38 48
Ватсон 48 59
Ветвления линии 18
Ветвления линии специальные случаи 19 31 50 51
Ветвления точки и полюсы см. «Полюсы и точки ветвления»
Вильямс 54 144 191 192
Винер 54 144 191 192
Винера — Хопфа уравнение (от комплексной переменной для точных решений), основы метода 49
Винера — Хопфа уравнение вывод из интегрального уравнения 82 191
Винера — Хопфа уравнение вывод из парных интегральных уравнений 171 172 249
Винера — Хопфа уравнение вывод методом Джонса 69 74 99 116 144 172
Винера — Хопфа уравнение обобщенное (от комплексной переменной для приближенных решений) 202
Винера — Хопфа уравнение обобщенное, решения 208 222
Винера — Хопфа уравнение обобщенное, формулировки задач 204 212 229 260 263
Винера — Хопфа уравнение, общие решения 94 104 251 256
Винера — Хопфа уравнение, решение для простых случаев 69 82
Винера — Хопфа уравнение, сведение к линейным алгебраическим уравнениям 197
Винера — Хопфа уравнения интегральные, вывод из физических соображений 105 151 200
Винера — Хопфа уравнения интегральные, вывод методом преобразований 14 79
Винера — Хопфа уравнения интегральные, вывод с помощью функции Грина 75 105 152
Винера — Хопфа уравнения интегральные, единственность решения 83 192
Винера — Хопфа уравнения интегральные, Милна интегральное уравнение 191
Винера — Хопфа уравнения интегральные, решение методом Винера — Хопфа 81 191 255
Винера — Хопфа уравнения интегральные, решение с помощью задачи Гильберта 193
Винера — Хопфа уравнения интегральные, сведение более общих случаев к уравнениям Фредгольма второго рода 259 260
Винера — Хопфа уравнения интегральные, сведение к повторным уравнениям Вольтерра 257
Винера — Хопфа уравнения интегральные, специальные уравнения 194 200
Винера — Хопфа уравнения, общее рассмотрение 173
Волновод плоский конечной длины 233
Волновод плоский полубесконечный см. «Полуплоскости две
Волновод плоский с неидеальными стенками 154
Волновод плоский с полосой конечной толщины, параллельной стенкам 238
Волновод плоский с полосой параллельной стенкам 136
Волновод плоский с системой штырей 197
Волновод плоский, бесконечной длины с полубесконечной диэлектрической пластиной 238
Волновод плоский, бесконечной длины с поперечной полосой 141 239
Волновод плоский, бесконечной длины со ступенькой 221 234
Волновод плоский, распространяющиеся и нераспространяющиеся типы волн 114
Волновод плоский, решение с помощью системы линейных алгебраических уравнений 197
Волновод цилиндрический конечной длины 233
Волновод цилиндрический полубесконечный электромагнитный 152
Волновод цилиндрический, бесконечной длины с неидеальными стенками 155
Волновод цилиндрический, излучение 127
Волновод цилиндрический, излучение из коаксиала 153 176
Волновод цилиндрический, падение волны на 134
Волновод цилиндрический, распространяющиеся и нераспространяющиеся типы волн 128
Волновод цилиндрический, содержащий полубесконечную трубу 140
Волновое уравнение 39
Волны на воде 110 155
Вольтерра интегральные уравнения 256 257 260
Вычисление бесконечных произведений 146 147
Вязкая среда 112 160
Гамма-функция 53
Гамма-функция выражающиеся через нее факторизации 53 190 194 243
Ганкеля функции, асимптотическое поведение 57
Ганкеля функции, интегральное представление 45
Гильберта задача 62 162
Гильберта задача, применение к интегральному уравнению 193
Граничные условия, содержащие произвольные функции 92 (см. также «Импедансные границы»)
Грин 110
Грина функция 75
Дейвисон 192
Дёч 38 48
Джонс 7 8 61 65 90 111 113 147 150 151 190 196 212 215 220 221 225 226 233 258
Джонса метод, общие замечания 7 61 86 91 114
Джонса метод, подробное рассмотрение на конкретном примере 65
Джонса метод, приближенные решения 202 263
Джонса метод, применение 116
Джонса метод, произвольные граничные условия 94
Дирака дельта-функция 56
Диск, волновое уравнение, высокие частоты 246
Диск, волновое уравнение, низкие частоты 240 258
Диск, уравнение Лапласа 190 258
Дифракция см. «Диск» «Волновод» «Полуплоскости» «Полосы
Дифракция методы, отличные от метода Винера — Хопфа 144 203
Диэлектрическая пластина 238 240
Единственность 86
Единственность и условие на ребре 64 89
Единственность решения интегральных уравнений 83 192
Заммерфельда задача о полуплоскости 61
Заммерфельда условия излучения 43
Звуковые волны см. «Волновод» «Полуплоскость»
Зейдель 192
Излучения условия на бесконечности 12 43
Иидзима 152
Импедансного типа границы, граничные условия см. «Импедансного типа границы»
Импедансного типа границы, обозначения 155
Импедансного типа границы, полоса, параллельная стенкам волновода 139
Импедансного типа границы, полоса, поперечная в волноводе 239
Импедансного типа границы, полуплоскость 98
Институт математических наук, Нью-Йорк, отчеты 265
Интегрального уравнения метод, общие замечания 7 59 86 91 263
Интегральные уравнения см. «Фредгольма интегральные уравнения» «Вольтерра «Винера
Иост 247
Источников распределения 56 65 102
Карлсон 119 153
Карп 190 (см. также «Вайнштейна — Карпа — Клеммова метод»)
Каррьер 110 113
Карслоу 87
Квантовомеханическая задача 247
Келлер 155
Кланкер 160
Клеммов 48 103 109 174
Клин из упругого материала 196
Клин, дифракция 247
Койтер 90 160 183 184 196
Конвекция тепла из плоской пластины 110
Контурные интегралы для разбиений на сумму и произведение 29
Контурные интегралы специального вида 43
Конус, уравнение волновое 246
Конус, уравнение Лапласа 189
Копсон 7 15 16 84 111 233 258
Копсона метод 258
Косинус-преобразование 169 239
Круглый волновод см. «Волновод цилиндрический»
Крыло двумерное 196
Крыло, занимающее четверть плоскости 110
Курганов 153 192
Лапласа преобразование 21 33 65 192
Лапласа преобразование, полная эквивалентность преобразованию Фурье 33 37
Лапласа типа уравнения 155 (см. также «Бигармоническое уравнение»)
Лапласа типа уравнения, уравнение Озеена 112
Лапласа уравнение в задаче о струе 160
Лапласа уравнение в полярных координатах 187 200
Лапласа уравнение как предел волнового уравнения 155
| Латтер 263
Лебега интеграл 34
Лебедева — Конторовича преобразование 170 240
Левин, Г. 31 54 133 150 152
Левин, Л. 152 203
Лейтнер 240 244 246
Леннокс 160
Линфут 199
Лиувилля теорема 17 50 70 83 119 132
Льюис 113
Магнус 199
Майлс 110
Марк 192
Маркувиц 141 153 203
Маршак 192
Мауэ 90 112
Мейер 246
Мейкснер 90
Мероморфные функции 52
Милна интегральное уравнение 191
Множитель 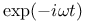 40 40
Морс 75 133 151 154 203
Мунк 110
Мусхелишвили, Н.И. 163 165 167 180 181
Навье — Стокса уравнение линеаризованное 112
Наложения метод 96 103
Неидеальная проводимость см. «Импедансного типа границы»
Оберхеттингер 48 199
Обозна в некоторых приближенных методах 206 222
Обозначения 9 21 40 67 101
Обход особых точек контуром интегрирования 42 56 102
Обход особых точек контуром интегрирования для преобразования по времени 57
Озеена уравнения 113
Отражения коэффициент в волноводе 127 132 138 143
Пак 8 160
Пападопулос 154 221
Параметр 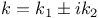 21 41 50 56 57 101 21 41 50 56 57 101
Парные интегральные уравнения для границ из трех частей 258
Парные интегральные уравнения для задач о полуплоскости 71
Парные интегральные уравнения для произвольно заданных граничных условий 93
Парные интегральные уравнения, общие соображения 61 92 249 263
Парные интегральные уравнения, решение методом преобразующего множителя 72 93 250
Парные интегральные уравнения, сведение к уравнению от комплексной переменной 171 173 249
Парные интегральные уравнения, содержащие бесселевы функции 8 250
Парные интегральные уравнения, точное решение общего случая 93 250
Парные интегральные уравнения, формулировка задач 15 71 171
Перевала метод 46
Переходные процессы 39 113
Перпендикулярные границы 202 205 212 234
Пирсон 152
Плачек 192
Племея формулы 59 166
Поглощающие границы см. «Импедансного типа границы»
Пограничный слой на плоской пластине 112
Поле в дальней зоне, примеры вычисления 122 127 133 217 232
Полосы и щели конечной толщины в волноводе 239
Полосы и щели конечной толщины и конечной длины 239
Полосы и щели конечной толщины полубесконечной длины 205 212
Полосы и щели конечной толщины, волновое уравнение, высокие частоты 207 229 246
Полосы и щели конечной толщины, волновое уравнение, низкие частоты 246
Полубесконечная плоскость см. «Полуплоскость»
Полуплоскости две параллельные сдвинутые 176
Полуплоскости три параллельные 176
Полуплоскости, бесконечная система, сдвинутые 153
Полуплоскость в упругой или вязкой среде 111
Полуплоскость из диэлектрика 240
Полуплоскость одиночная конечной толщины 205 212
Полуплоскость одиночная, бесконечно тонкая, основная задача дифракции (Зоммерфельда) 61
Полуплоскость с конечной проводимостью 98
Полуплоскость с фланцем 207
Полуплоскость, дифракция электромагнитной волны на 111
Полуплоскость, излучение из двух параллельных 122
Полуплоскость, обобщения основной задачи дифракции 64
Полуплоскость, падение волны на 116 144 145
Полуплоскость, решение с помощью системы линейных алгебраических уравнений 198
Полюсы и точки ветвления 59 153 233
Полярные координаты в задаче об упругом клине 196
Полярные координаты в уравнении Лапласа 187 200
Полярные координаты в уравнении стационарном волновом 169 242
Поперечное сечение рассеяния диска 246
Поправка на конец, толстая полубесконечная пластина 220
Поправка на конец, цилиндрическая труба 132
Преобразование 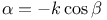 , применение для вычисления интегралов 45 , применение для вычисления интегралов 45
Преобразование 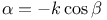 , применение для разбиения на сумму 59 , применение для разбиения на сумму 59
Преобразование 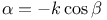 , применение к задаче о дифракции на полуплоскости 199 , применение к задаче о дифракции на полуплоскости 199
Преобразование 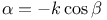 , применение к задаче о клине 247 , применение к задаче о клине 247
Преобразующего множителя метод 72 93 249
Приближенная факторизация 182
Приближенные методы 202 263
Приближенные методы для интегральных уравнений 258 260
Приближенные методы для полос и щелей 229
Приближенные методы для толстых пластин 212
Приближенные методы, различные формулировки 205
Приливы в шхерах 110
Проверка решения 86
Радиоволн распространение над морской береговой линией 109
Разбиение на сумму в приближенных решениях 203 212
Разбиение на сумму с применением преобразования 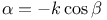 59 59
Разбиение на сумму функции 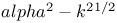 32 59 32 59
Разбиение на сумму функции с полюсами 51
Разбиение на сумму, общие теоремы 24
Разбиение на сумму, общие формулы для конкретных случаев 29
Разбиение на сумму, применения 95 203 212 224 256
Разделение переменных 11 168 170
Рассек 233
Расходящиеся интегралы 78
Регулярность преобразований в комплексной плоскости 23
Регулярность функций, определенных интегралами 21
Синьор 98 100 108 109 155
Системы уравнений Винера — Хопфа в двумерных волноводных задачах 140 176
Системы уравнений Винера — Хопфа в задаче для электромагнитного цилиндрического волновода 152
Системы уравнений Винера — Хопфа в электромагнитной задаче для полуплоскости 111
Системы уравнений Винера — Хопфа, общая теория 175
Системы уравнений линейных алгебраических в волноводной задаче 198
Системы уравнений линейных алгебраических в задаче о полуплоскости 199
Системы уравнений линейных алгебраических в приближенных решениях 209 215 234 244
Системы уравнений линейных алгебраических, получающиеся из систем уравнений Винера — Хопфа 177
Системы уравнений линейных алгебраических, решение частных случаев 196 197
Смешанные граничные условия 11
Смешанные граничные условия для границы из двух частей, общая теория 168
Смешанные граничные условия для границы из трех частей 207 229 258
Смешанные граничные условия, решение типичного примера 92
Снеддон 8 12 111 192 258 264
Спаренберг 193 194
Стационарное волновое уравнение 39
Стержень полубесконечный 221
Стержень твердый, цилиндрический, конечной длины 240
Струи 160
Таблицы для вычислений 8 141 151
Титчмарш 12 15 18 22 52 54 192 194
Титчмарша метод 195
Трантер 12
У, Тай-те 264
Уиддер 38 48
Уиттекера функции 226 240
Упругая среда, дифракция из полуплоскости, расположенной в упругой среде 111 (см. также «Бигармоническое уравнение»)
Упругая среда, напряжения на клине со смешанными граничными условиями 196
Условия на ребре 64 89
Условия на ребре, литература 90
Уэйц 155
Уэлс 240 244
Факторизация на множители 25
Факторизация на множители приближенная 182
Факторизация на множители функции 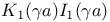 130 150 130 150
Факторизация на множители функции 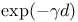 32 32
Факторизация на множители функций 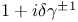 107 186 107 186
Факторизация на множители функций 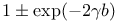 119 119
Факторизация на множители, общие теоремы 26 53
Факторизация на множители, применение преобразования 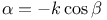 59. 59.
Факторизация на множители, содержащая гамма-функцни 53 190 194 243
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



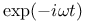
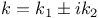
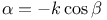 , применение для вычисления интегралов
, применение для вычисления интегралов