It is well known that the classical sequence spaces co and Ip (1 <= p <
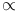
) have, up to equivalence, just one symmetric basis. On the other hand, there are examples
of Orlicz sequence spaces which have uncountably many mutually nonequivalent
symmetric bases. Thus in [4], p. 130, the question is asked whether
there is a Banach space with, up to equivalence, more than one symmetric basis,
but not uncountably many. In this paper we answer the question positively, by
exhibiting a Banach space with, up to equivalence, precisely two symmetric
bases.
 |
|
О проекте
|
|
О проекте


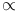 ) have, up to equivalence, just one symmetric basis. On the other hand, there are examples
) have, up to equivalence, just one symmetric basis. On the other hand, there are examples
