|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Johnson N., Kotz S., Kemp A.W. Ч Univariate discrete distributions |
|
|
 |
| ѕредметный указатель |
Discrete distributions, Ising Ч Stevens 88 423Ч424
Discrete distributions, Katti Type 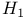 330Ч331 330Ч331
Discrete distributions, Katti Type 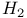 92 206 282 339 92 206 282 339
Discrete distributions, Kempton's log-series generalization 02
Discrete distributions, Laplace Ч Haag matching distribution 2 410Ч411
Discrete distributions, leads in coin tossing 274Ч275
Discrete distributions, Lexian 141
Discrete distributions, log-zero-Poisson 317Ч318 334
Discrete distributions, lost-games 96 281 445Ч447
Discrete distributions, Lueders Formel I 231
Discrete distributions, Lueders Formel II 231Ч232
Discrete distributions, Markov Ч Polya 240 283
Discrete distributions, Marlow's factorial 88 104 279
Discrete distributions, Morlat's generalized Poisson 195Ч191 324
Discrete distributions, Morse 454
Discrete distributions, Naor 447Ч448
Discrete distributions, negative binomial mixtures 242Ч243 329 330
Discrete distributions, negative hypergeometric 83 88 92 239Ч242 245 252 254Ч255 270Ч271
Discrete distributions, Neyman Types B and C 88 387
Discrete distributions, noncentral negative binomial 148 232Ч233
Discrete distributions, Pascal see Negative binomial distribution
Discrete distributions, Pascal Ч Poisson 233Ч234 388Ч389 402
Discrete distributions, Poisson and binomial mixture 321Ч322
Discrete distributions, Poisson beta 92 330Ч331 338 386
Discrete distributions, Poisson binomial 232
Discrete distributions, Poisson Lexis 142
Discrete distributions, Poisson lognormal 301 332
Discrete distributions, Poisson mixture of binomials 336
Discrete distributions, Poisson mixture of negative binomials 329Ч330
Discrete distributions, Poisson mixture of Poissons see Neyman Type A
Discrete distributions, Poisson negative binomial 231Ч232
Discrete distributions, Poisson rectangular 88 330
Discrete distributions, Poisson truncated gamma 331
Discrete distributions, Poisson truncated normal 332 361Ч362
Discrete distributions, Poisson Ч Lindley 148 332Ч333
Discrete distributions, Poisson's exponential limit distribution 449
Discrete distributions, Poisson-inverse Gaussian 455Ч457
Discrete distributions, Poisson-stopped sums 188Ч189 351Ч356
Discrete distributions, Poissonian trials 138Ч140
Discrete distributions, poly-nacci 427
Discrete distributions, Polya 88 92 200 205 244Ч249
Discrete distributions, Polya Ч Eggenberger 88 200 205
Discrete distributions, pseudo-Euler 198
Discrete distributions, quasi-binomial 102
Discrete distributions, quasi-hypergeometric 101
Discrete distributions, quasi-Polya 101
Discrete distributions, random-walk 98 445
Discrete distributions, record value distributions 453Ч455
Discrete distributions, rectangular 272Ч274 342 430 432
Discrete distributions, Riemann zeta 466Ч469
Discrete distributions, riff-shuffle 234Ч235
Discrete distributions, Sichel distributions 455Ч457
Discrete distributions, Skellam's gene frequency 457Ч459
Discrete distributions, Stevens Ч Craig 92 104 418
Discrete distributions, Stirling of the first kind 88 300
Discrete distributions, Stirling of the second kind 88 190Ч191
Discrete distributions, sub-Poisson 193 206
Discrete distributions, Subrahmaniams' generalized Neyman 388Ч389
Discrete distributions, super-Poisson 193
Discrete distributions, Tanner Ч Borel 96 98 189 277 394Ч396 453 469
Discrete distributions, Thomas 88
Discrete distributions, trigamma 436Ч437
Discrete distributions, univariate factorial multinomial 462Ч463
Discrete distributions, univariate multinomial 460Ч462
Discrete distributions, univariate negative factorial multinomial 462Ч463
Discrete distributions, univariate negative multinomial 461Ч463 .
Discrete distributions, Waring 88 104 278Ч279
Discrete distributions, weighted binomial 145Ч147
Discrete distributions, weighted negative binomial 230Ч231
Discrete distributions, Yule 88 104 275Ч278 469
Discrete distributions, zeta 466Ч469
Discrete distributions, Zipf 466Ч469
Discrete linear exponential distribution 70 311
Discrete random variable 36
Dispersion: overdispersion 89 94 157 198 326
Dispersion: underdispersion 89 94 157 198
Displacement operators (backward, central, forward) 8Ч9
Distinguishable particles 420
Distribution function see Cumulative distribution function (cdf)
Distributional types: "par grappes" 188 356
Distributional types: ascertained 90 94 146
Distributional types: compound 188 344
Distributional types: conditional 37 112 161 279Ч280
Distributional types: deflated 186Ч187 312Ч318
Distributional types: discrete linear exponential 70 311
Distributional types: envelope 64
Distributional types: group size 287 447
Distributional types: inflated 186Ч187 312Ч318
Distributional types: interrupted 443Ч445
Distributional types: lattice 69
Distributional types: matching 409Ч414
Distributional types: mixing 53Ч54 305Ч342
Distributional types: mixture 53Ч54 305Ч342
Distributional types: modified 186Ч187 300 312Ч318
Distributional types: order k see Distributions of order k
Distributional types: parent distribution 448
Distributional types: partial sums 448Ч451
Distributional types: positive 135Ч136 168 181 282
Distributional types: proper distribution 35
Distributional types: renewal 451
Distributional types: size-biased 146
Distributional types: STER 92 244 248 449Ч450
Distributional types: stopped sums 188Ч189 233 343Ч403
Distributional types: target 62 64
Distributional types: truncated 52Ч53 135Ч137 181Ч186 225Ч227 299Ч300
Distributional types: waiting time 200 240 241
Distributional types: weighted 90 94 145Ч147 230Ч231
Distributions of order k: beta-binomial 284
Distributions of order k: beta-negative binomial 284
Distributions of order k: binomial I 431
Distributions of order k: binomial II 432
Distributions of order k: binomial III 432
Distributions of order k: compound Poisson 430
Distributions of order k: extended 189 432
Distributions of order k: further 432
Distributions of order k: generalized Waring 284 432
Distributions of order k: geometric 427Ч428
Distributions of order k: hypergeometric 284 432
Distributions of order k: inverse hypergeometric 432
Distributions of order k: inverse Polya 284 432
Distributions of order k: logarithmic I 303 429
Distributions of order k: logarithmic II 303 432
Distributions of order k: negative binomial I 303 428
Distributions of order k: negative binomial II 303 430
Distributions of order k: negative binomial III 303 432
Distributions of order k: negative hypergeometric 284
Distributions of order k: Poisson 189 429Ч430
Distributions of order k: Polya 284 432
Distributions of order k: waiting time 284
Diversity 298
Ehrenfest model of heat exchange 464
Elementary functions: Estimable parameters of finite mixtures 310Ч311
Elementary functions: generalized hypergeometric representations 24
Elementary functions: hypergeometric representations 18Ч19
Estimation: even-points method 361
Estimation: first-moment equation 60 73 76
Estimation: generalized/modified/partial/penalized maximum-likelihood methods 60
Estimation: maximum likelihood 59 60 73 76 311 350
Estimation: mean and zero-frequency method 217
Estimation: method of moments 59Ч60 311
Estimation: minimum chi-square method 217 391
Estimation: minimum variance unbiased 58 73Ч74 76
Estimation: pseudo-likelihood methods 60
Estimator see also Estimation
Estimator, asymptotically efficient 58
Estimator, asymptotically unbiased 57
Estimator, biased 57
Estimator, consistent 58
Estimator, efficient 58
Estimator, relative efficiency 57
| Estimator, sufficient 58
Estimator, unbiased 57
Euler transformations 18
Euler's constant 5 8
Euler's integral 18
Everett's central difference formula 10
Exceedances 240Ч241 274
Exchangeable events 406
Exhaustive events 34
Expansions: Barnes 6
Expansions: binomial 3.4
Expansions: Camp Ч Paulson 117 210 212
Expansions: Edgeworth 162
Expansions: Faa di Bruno 346 430
Expansions: Gram Ч Charlier 117 210Ч211 442Ч443
Expansions: Lagrange 13 96 97 396
Expansions: multinomial 4
Expansions: Stirling 6
Expansions: Waring 243 278
Expected value 39Ч40
Faa di Bruno's formula 346 430
Factorial cumulants 45Ч46 71Ч72 89 94 326Ч327 348 354 355
Factorial moments 43Ч44 50 71 75 89 91Ч93 326 348 353 354 408
Failure rate 36 111 160 209 290
Families 69Ч104
Families, Abel 101Ч102
Families, Bissinger (STER) distributions 92 244 248 449Ч450
Families, Crow and Bardwell 80
Families, difference equation 77
Families, discrete linear-exponential 70
Families, discrete Pearson 77
Families, extended Crow and Bardwell 80 87
Families, extended Katz 79Ч80 87
Families, factorial series distributions 102Ч104
Families, general Dirichlet series 74
Families, generalized factorial series distributions 104
Families, generalized power series distributions (GPSD) 70Ч74
Families, Gould 100Ч101
Families, Katz 77Ч80 87
Families, Kemp's hypergeometric factorial distributions 85 91Ч95 338Ч339
Families, Kemp's hypergeometric probability distributions 80 84Ч91 339Ч340
Families, Kemp's hypergeometric recast distributions 85 94Ч95
Families, Khatri and Patel Type A, B. and — 400Ч402
Families, Lagrangian expansion 75 96Ч100
Families, modified power series distributions (MPSD) 74Ч77
Families, multiparameter power series distributions 75
Families, Ord 81Ч84
Families, Patil's two-parameter power series distributions 74
Families, Poisson power series distributions 356
Families, Poisson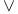 Katz family 382 391 Katz family 382 391
Families, Pollaczek Ч Geiringer 356
Families, power series distributions (PSD) 70Ч77
Families, q-series 140 304 434Ч435
Families, Steyn's two-parameter PSD 75 459Ч460
Families, Sundt and Jewel 80Ч81
Fermi Ч Dirac statistics 405 420Ч422
Fiducial limits 61
Finite difference calculus 8Ч11
Finite mixtures of discrete distributions 53 306
Finite mixtures of discrete distributions, applications 309Ч312
Finite mixtures of discrete distributions, binomials 319Ч321
Finite mixtures of discrete distributions, other distributions 321Ч322
Finite mixtures of discrete distributions, Poissons 318Ч319
Force of mortality 36
Fourier transform 27
Frechet inequalities 408Ч409
Functions (mathematical): basic hypergeometric function 31Ч32
Functions (mathematical): Bessel of the first kind 16
Functions (mathematical): beta 7
Functions (mathematical): confluent hypergeometric function 19Ч22
Functions (mathematical): digamma 7
Functions (mathematical): error functions 16 21
Functions (mathematical): gamma 4Ч6
Functions (mathematical): Gaussian hypergeometric 17Ч19
Functions (mathematical): generalized hypergeometric 22Ч24
Functions (mathematical): hypergeometric 17Ч19
Functions (mathematical): incomplete beta 15
Functions (mathematical): incomplete gamma 14
Functions (mathematical): Kummer 19Ч22
Functions (mathematical): modified Bessel of the first kind 16Ч17
Functions (mathematical): modified Bessel of the third (second) kind 30 455
Functions (mathematical): normal distribution 16
Functions (mathematical): psi 7
Functions (mathematical): q-hypergeometric series 31Ч32
Functions (mathematical): Riemann zeta 29Ч30
Functions (mathematical): trigamma 7
Gauss's multiplication theorem 6
Gauss's summation theorem 17
Generalized distributions as mixtures 323Ч325 345 354
Generalized hypergeometric distributions 244Ч256
Generalized hypergeometric distributions, limiting forms 255Ч256
Generalized hypergeometric distributions, models 245 247Ч249
Generalized hypergeometric distributions, moments 249Ч253
Generalized hypergeometric distributions, tail properties 254Ч255
Generalized variance 58
Generating functions: central (corrected) moment 41 50 71 89 93Ч94
Generating functions: cumulant 44Ч45 50 71Ч72 326Ч327
Generating functions: exponential 419
Generating functions: factorial cumulant 45 71Ч72.
Generating functions: factorial moment 44 50 71 89 91 93 326 408
Generating functions: moment (uncorrected) 40 50 71 89 93Ч94
Generating functions: probability 50 89 93 408
Geometric distribution 88 98 147 200 201Ч203 220Ч223 240 279 287 316 322 378 441
Geometric distribution, applications 203
Geometric distribution, characterizations 201 202 220Ч223
Geometric distribution, computer generation 66 67
Geometric distribution, exponential relationship 201
Geometric distribution, genesis 201Ч202
Geometric distribution, infinite divisibility 202
Geometric distribution, Markovian property 201
Geometric distribution, moment and other properties 201 202
Geometric distribution, order statistics 202
Geometrical concepts 55Ч56
Goodness-of-fit 57
Goodness-of-fit, Gram Ч Charlier approximation 117 210Ч211 442Ч443
Goodness-of-fit, Pearson's chi-square test 132Ч133 173 366 388
Gurland's theorem 324Ч325
Half-mode 42
Hazard rate (increasing/decreasing) 36
Heine's theorem 32
Hermite distribution 88 357Ч364 366 391 441
Hermite distribution, estimation 360Ч361
Hermite distribution, genesis 332 357 359Ч361
Hermite distribution, moment and other properties 357 358Ч360
Heterogeneity 344
Homoscedasticity 47
Hypergeometric distributions 83 88 92 104 120 134 138 237Ч284 334Ч335 341Ч342 421 423Ч424
Hypergeometric distributions, applications 269Ч272
Hypergeometric distributions, approximations, bounds, and tables 256Ч262
Hypergeometric distributions, characterizations 266Ч269
Hypergeometric distributions, classical 83 84 237Ч238 238Ч239 245 254 262Ч264 269Ч270
Hypergeometric distributions, comparison with other distributions 135 255Ч256
Hypergeometric distributions, computation of probabilities 262
Hypergeometric distributions, computer generation 67Ч68
Hypergeometric distributions, estimation 262Ч266
Hypergeometric distributions, extended hypergeometric 279Ч282
Hypergeometric distributions, geneses and history 112 237Ч244
Hypergeometric distributions, hypergeometric mixture of binomials 337
Hypergeometric distributions, inverse (negative) hypergeometric 83 88 239Ч242 245 254 264Ч266 270Ч271
Hypergeometric distributions, limiting 138 179 228
Hypergeometric distributions, mixed hypergeometric distributions 322 342
Hypergeometric distributions, moment properties 249Ч253
Hypergeometric distributions, noncentral hypergeometric 282Ч283
Hypergeometric distributions, other properties 253Ч256
Hypergeometric distributions, positive hypergeometric 282
Hypergeometric distributions, tail properties 253Ч255
Hypergeometric distributions, Types I, II, III. and IV 246Ч256
Hypergeometric distributions, waiting-time distribution 240 241
Hypothesis testing 57
Identifiability of mixtures 310Ч311 323
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



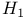
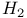
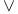 Katz family
Katz family