|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hedenmalm H., Korenblum B., Zhu K. — Theory of Bergman spaces |
|
|
 |
| Предметный указатель |
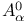 , the Bergman — Nevanlinna class 98 131 , the Bergman — Nevanlinna class 98 131
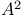 -subinner function 52 -subinner function 52
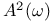 , weighted Bergman space 245 , weighted Bergman space 245
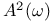 -inner function 270 -inner function 270
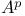 -inner function 52 -inner function 52
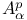 -inner function 52 -inner function 52
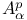 -subinner function 87 -subinner function 87
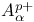 , limit of Bergman spaces 130 , limit of Bergman spaces 130
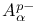 , limit of Bergman spaces 130 , limit of Bergman spaces 130
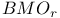 42 42
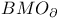 45 45
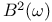 , large weighted Bergman space 245 , large weighted Bergman space 245
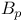 , the Besov space 23 , the Besov space 23
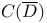 13 13
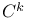 60 60
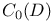 13 13
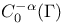 137 137
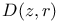 , hyperbolic disk 38 , hyperbolic disk 38
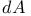 , the normalized area element 1 , the normalized area element 1
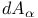 , the weighted area element 2 , the weighted area element 2
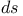 , normalized arc length measure 59 104 , normalized arc length measure 59 104
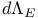 , push-out measure 114 , push-out measure 114
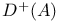 , upper asymptotic , upper asymptotic  -density 105 -density 105
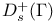 , upper Seip density 147 , upper Seip density 147
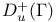 , uniform separating upper asymptotic , uniform separating upper asymptotic  -density of -density of  140 140
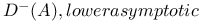 \kappa$-density 105 \kappa$-density 105
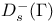 , lower Seip density 153 , lower Seip density 153
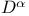 , “fractional differentiation” 18 , “fractional differentiation” 18
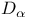 , “fractional integration” 19 , “fractional integration” 19
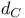 Euclidean metric on the plane 105 Euclidean metric on the plane 105
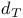 , circle metric 104 , circle metric 104
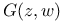 , Green function for the Laplacian 60 , Green function for the Laplacian 60
![$G[f]$](/math_tex/e679c18eb86110d1483864eb74078de482.gif) , Green potential 60 , Green potential 60
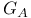 , zero divisor for A 57 , zero divisor for A 57
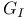 , the extremal function for I 57 , the extremal function for I 57
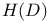 , the space of all holomorphic functions 18 , the space of all holomorphic functions 18
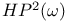 251 251
 , the Hardy space 54 , the Hardy space 54
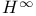 2 2
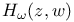 , the harmonic compensator 266 , the harmonic compensator 266
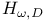 , harmonic compensator 254 , harmonic compensator 254
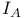 , zero-based invariant subspace 55 , zero-based invariant subspace 55
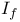 , invariant subspace generated by f 56 , invariant subspace generated by f 56
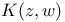 , the Bergman kernel 6 , the Bergman kernel 6
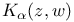 , the Bergman kernel for standard weights 6 , the Bergman kernel for standard weights 6
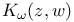 , weighted Bergman kernel 245 , weighted Bergman kernel 245
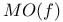 , “mean oscillation” 43 , “mean oscillation” 43
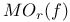 , mean oscillation 42 , mean oscillation 42
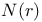 , counting function 100 , counting function 100
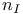 , common multiplicity of zero at the origin 56 , common multiplicity of zero at the origin 56
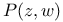 , Poisson kernel 29 , Poisson kernel 29
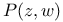 , the Poisson kernel 114 217 , the Poisson kernel 114 217
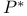 , the sweep operator 87 , the sweep operator 87
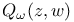 , weighted harmonic Bergman kernel 252 , weighted harmonic Bergman kernel 252
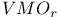 46 46
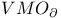 46 46
 , the hyperbolic metric 16 , the hyperbolic metric 16
 , invariant Laplacian 32 , invariant Laplacian 32
 , the Laplacian 32 , the Laplacian 32
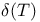 , diagonal 253 , diagonal 253
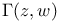 , biharmonic Green function 62 , biharmonic Green function 62
![$\Gamma[f]$](/math_tex/0b1b8930fdf3dbade8244d54e159d8ad82.gif) , biharmonic Green potential 62 , biharmonic Green potential 62
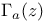 , approximate Stolz angle 111 , approximate Stolz angle 111
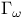 , the weighted biharmonic Green function 242 , the weighted biharmonic Green function 242
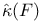 , Beurling — Carleson characteristic 104 , Beurling — Carleson characteristic 104
 -absolutely continuous 201 -absolutely continuous 201
 -area 148 -area 148
 -bound 194 -bound 194
 -bounded above 194 -bounded above 194
 -density 105 -density 105
 -smooth 201 -smooth 201
 -variation 194 -variation 194
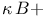 194 194
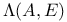 , partial logarithmic Blaschke sum on E 105 , partial logarithmic Blaschke sum on E 105
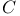 , the complex plane 1 , the complex plane 1
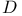 , the open unit disk 1 , the open unit disk 1
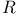 , the real line 1 , the real line 1
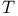 , the unit circle 1 , the unit circle 1
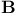 , the Berezin transform 29 , the Berezin transform 29
$\mathbf B_\alpha, the weighted Berezin transform 29
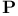 , Bergman projection 6 , Bergman projection 6
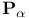 , weighted Bergman projection 6 , weighted Bergman projection 6
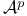 , the Bergman spaces 6 , the Bergman spaces 6
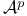 -outer function 190 191 -outer function 190 191
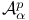 , the standard weighted Bergman space 2 , the standard weighted Bergman space 2
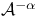 , standard growth space 110 , standard growth space 110
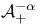 , limit of growth spaces 112 , limit of growth spaces 112
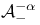 , limit of growth spaces 112 , limit of growth spaces 112
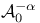 , , small growth space 110 137 , , small growth space 110 137
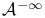 , the big growth space 110 , the big growth space 110
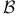 , the Bloch space 13 , the Bloch space 13
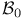 , the little Bloch space 13 , the little Bloch space 13
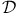 , the Dirichlet space 25 , the Dirichlet space 25
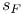 , Stolz star 105 , Stolz star 105
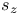 , Stolz angle 104 , Stolz angle 104
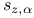 , Stolz angle with aperture , Stolz angle with aperture  106 106
 , the gradient 51 , the gradient 51
 , harmonic measure 218 , harmonic measure 218
 , weight 242 244 , weight 242 244
 -mean value disk 255 -mean value disk 255
 , the pseudohyperbolic metric 16 , the pseudohyperbolic metric 16
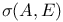 , partial Blaschke sum on E 105 , partial Blaschke sum on E 105
 2 2
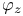 , the Moebius involution 6 , the Moebius involution 6
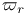 , harmonic measure 255 , harmonic measure 255
Absolutely continuous measure 201
Admissible 122
Analytic projection 12
Aperture 104 106
Arc length 104
Arc length, normalized 104
Arithmetic-geometric mean inequality 101
Asymptotic  -density, lower 105 -density, lower 105
Asymptotic  -density, upper 105 -density, upper 105
Atomic singularity 59
Balayage-type estimate 112
Berezin transform 28
Bergman kernel 6
Bergman metric 16
Bergman projection 6
Bergman space 2
Bergman — Nevanlinna class 98 131
Besov space 24 50
Beurling — Carleson characteristic 104
Beurling — Carleson set 104 200
Beurling's theorem 176
Beurling-type theorem 181
Bi-harmonic Green function 62
Bi-harmonic Green potential 62
Biharmonic Green function 59 242
Blaschke product 26
Bloch space 13
BMO 42
BMO in the Bergman metric 42
BMOA 13
Bounded  -variation 194 -variation 194
building blocks 219
Caratheodory-Schur theorem 87
Carleson measure 38
Carleson square 106 240
Cayley transform 113 165 167
Complementary arcs 104
Concave operator 182
Concave sequence 183
Concavity-type property of the biharmonic Green function 273
Conjugate exponent 18 160
Contractive divisibility property 59
Contractive multiplier 54
Contractive zero divisors 71
Covering 125 204
| Cyclic function 190
Cyclic invariant subspace 56
Cyclic vector 78 85 190
density 104
Dirichlet space 25
Division property 189
Domination 190 191
Duality theorem of Linear Programming 124 204
Edge point in polyhedron 124
Eigenfunctions 36
Eigenvalue 37
Elementary factors 131
entropy 104
Exact type 111
Expansive multiplier property 59 66 70
Extraneous zero 72
Extremal function 57
Extremal problem 26 55 56 195
Extremal problem for I 56
Factorization 78
Fejer kernel 87
Fractional differentiation 18
Fractional integration 18
Functions of bounded variation 195
Gap sequence 15
Garsia's lemma 42
Generation 233
Geometric progression 107
Green function 59
Green potential 60
Green's formula 59
Growth space 110
Hadamard's variational formula 255 257
Hankel operator 49
Hardy space 12 54 78
Harmonic compensator 254 266
Harmonic conjugate 26
Harmonic majorant 55
Harmonic measure 218 219 225 232
Helly selection theorem 195
Herglotz measure 201
Herglotz transform 259
Homogeneous decomposition 178
Hurwitz's theorem 77
Hyperbolic center 42
Hyperbolic disk 38
Hyperbolic exponential type 111
Hyperbolic metric 16
Hyperbolic radius 42
INDEX 176
Index n 176
Index of an invariant subspace 176
Inner function 52 78
Inner function for Bergman spaces 53
Inner space 180
Inner-outer factorization 78
Interpolating sequence 50 136
Interpolation problem 137
Invariant Laplacian 32
Invariant subspace 55
Invariant subspace problem 187
Iteration scheme 222
Jensen's formula 98
Jensen-type inequality 116
Koebe function 260
Lacunary series 15
Laplace equation 62
Laplace — Beltrami operator 33
Laplacian 32 Laplacian invariant
Linear programming 119
Linear Programming, duality theorem 124 204
Little Bloch space 13
Localization trick 230
Logarithmic entropy 194
Logarithmically subharmonic 94 242 244
Lower asymptotic  -density 105 -density 105
Lower Seip density 153
Lunula 227
Maximal inner space 187
Mean oscillation 42
Min-max equation 123
Minimal type 111
Moebius group 6
Moebius map 6
Moebius transformation 16
Mushroom 231
Mushroom forest 230
Mushroom hat 232
Mushroom stem 231
Nonoverlapping arcs 211
Normalized arc length 59 104
Oblique projection 119
Optimization problem 123
Outer function 190
Perturbation 139
Poincare metric 16
Point-evaluation 2
Poisson extension 114
Poisson formula 29
Poisson kernel 29 114
Poisson solver 273
Poisson transform 28 29 114 273
Positive function 2
Positive measure 2
Premeasure 190 193
Pseudohyperbolic metric 16
Push-out measure 114
Quasi-Banach space 2
Quasi-similar operators 188
Regular sequence 177
Reproducing for the origin 242
Reproducing kernel 57 242
Residue theorem 76
Restriction operator 155
Reverse triangle inequality 177
Sampling sequence 136
Schur's test 9 11
Seip density, lower 153
Seip density, upper 147
Separated sequence 39 50 138
Sequence of interpolation 136
Sequence of sampling 136
Sesquiholomorphic 252
Similar operators 188
Simple covering 125 204
Singly generated invariant subspace 56
Singular inner function 59
Singular measure 201
Spectral mapping theorem 37
Stieltjes integral 195
Stolz angle 104
Stolzstar 105
Strictly positive 2
Subinner function 86
Suppressive weight 273
Sweep of a function 88 264
Toeplitz operator 49
Truncation 202
Type, hyperbolic exponential 111
Uniform separating upper asymptotic  -density 140 -density 140
Uniform upper asymptotic  -density 146 -density 146
Uniformly discrete 39
Upper asymptotic  -density 105 -density 105
Upper Seip density 147
Variational argument 56
Variational formula 255
VMO 42
Weakly cyclic 201
Weierstrass factorization 131
Weighted Bergman kernel 6
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



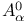 , the Bergman — Nevanlinna class
, the Bergman — Nevanlinna class 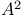 -subinner function
-subinner function 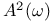 , weighted Bergman space
, weighted Bergman space 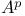 -inner function
-inner function 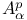 -inner function
-inner function 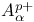 , limit of Bergman spaces
, limit of Bergman spaces 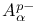 , limit of Bergman spaces
, limit of Bergman spaces 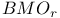
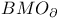
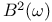 , large weighted Bergman space
, large weighted Bergman space 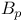 , the Besov space
, the Besov space 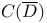
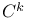
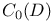
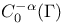
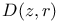 , hyperbolic disk
, hyperbolic disk 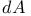 , the normalized area element
, the normalized area element 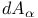 , the weighted area element
, the weighted area element 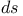 , normalized arc length measure
, normalized arc length measure 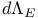 , push-out measure
, push-out measure 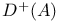 , upper asymptotic
, upper asymptotic  -density
-density 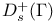 , upper Seip density
, upper Seip density 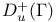 , uniform separating upper asymptotic
, uniform separating upper asymptotic 
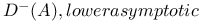 \kappa$-density
\kappa$-density 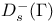 , lower Seip density
, lower Seip density 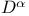 , “fractional differentiation”
, “fractional differentiation” 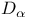 , “fractional integration”
, “fractional integration” 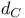 Euclidean metric on the plane
Euclidean metric on the plane 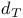 , circle metric
, circle metric 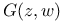 , Green function for the Laplacian
, Green function for the Laplacian ![$G[f]$](/math_tex/e679c18eb86110d1483864eb74078de482.gif) , Green potential
, Green potential 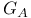 , zero divisor for A
, zero divisor for A 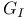 , the extremal function for I
, the extremal function for I 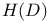 , the space of all holomorphic functions
, the space of all holomorphic functions 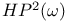
 , the Hardy space
, the Hardy space 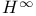
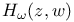 , the harmonic compensator
, the harmonic compensator 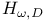 , harmonic compensator
, harmonic compensator 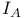 , zero-based invariant subspace
, zero-based invariant subspace 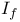 , invariant subspace generated by f
, invariant subspace generated by f 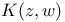 , the Bergman kernel
, the Bergman kernel 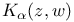 , the Bergman kernel for standard weights
, the Bergman kernel for standard weights 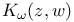 , weighted Bergman kernel
, weighted Bergman kernel 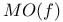 , “mean oscillation”
, “mean oscillation” 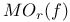 , mean oscillation
, mean oscillation 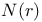 , counting function
, counting function 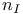 , common multiplicity of zero at the origin
, common multiplicity of zero at the origin 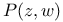 , Poisson kernel
, Poisson kernel 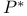 , the sweep operator
, the sweep operator 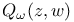 , weighted harmonic Bergman kernel
, weighted harmonic Bergman kernel 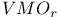
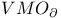
 , the hyperbolic metric
, the hyperbolic metric  , invariant Laplacian
, invariant Laplacian 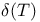 , diagonal
, diagonal 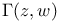 , biharmonic Green function
, biharmonic Green function ![$\Gamma[f]$](/math_tex/0b1b8930fdf3dbade8244d54e159d8ad82.gif) , biharmonic Green potential
, biharmonic Green potential 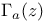 , approximate Stolz angle
, approximate Stolz angle 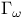 , the weighted biharmonic Green function
, the weighted biharmonic Green function 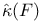 , Beurling — Carleson characteristic
, Beurling — Carleson characteristic 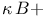
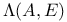 , partial logarithmic Blaschke sum on E
, partial logarithmic Blaschke sum on E 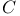 , the complex plane
, the complex plane 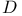 , the open unit disk
, the open unit disk 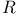 , the real line
, the real line 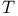 , the unit circle
, the unit circle 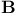 , the Berezin transform
, the Berezin transform 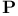 , Bergman projection
, Bergman projection 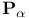 , weighted Bergman projection
, weighted Bergman projection 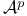 , the Bergman spaces
, the Bergman spaces 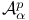 , the standard weighted Bergman space
, the standard weighted Bergman space 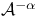 , standard growth space
, standard growth space 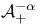 , limit of growth spaces
, limit of growth spaces 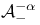 , limit of growth spaces
, limit of growth spaces 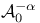 , , small growth space
, , small growth space 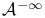 , the big growth space
, the big growth space 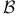 , the Bloch space
, the Bloch space 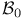 , the little Bloch space
, the little Bloch space 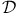 , the Dirichlet space
, the Dirichlet space 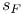 , Stolz star
, Stolz star 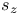 , Stolz angle
, Stolz angle 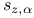 , Stolz angle with aperture
, Stolz angle with aperture 
 , the gradient
, the gradient  , harmonic measure
, harmonic measure  , the pseudohyperbolic metric
, the pseudohyperbolic metric 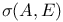 , partial Blaschke sum on E
, partial Blaschke sum on E 
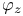 , the Moebius involution
, the Moebius involution 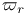 , harmonic measure
, harmonic measure  -density
-density