|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Eliashberg Y., Mishachev N. — Introduction to the h-Principle |
|
|
 |
| Предметный указатель |
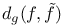 184 184
 10 10
 8 8
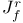 8 8
 -mersion 62 -mersion 62
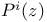 159 159
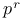 9 9
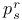 10 10
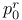 9 9
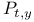 148 148
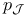 73 73
 73 73
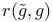 183 183
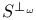 70 70
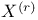 9 9
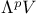 72 72
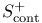 94 94
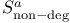 97 97
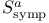 93 93
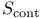 94 94
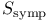 93 93
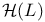 73 73
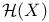 74 74
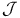 93 93
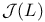 72 72
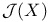 74 74
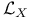 79 79
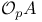 9 9
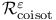 167 167
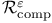 168 168
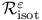 167 167
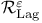 167 167
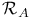 165 165
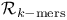 160 160
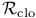 49 49
 166 166
 168 168
 87 87
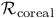 168 168
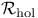 126 126
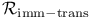 131 131
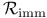 48 48
 87 87
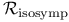 124 124
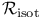 166 166
 124 166 124 166
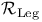 87 87
 168 168
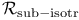 124 124
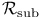 48 48
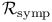 166 166
 130 130
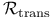 130 130
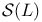 70 70
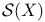 74 74
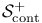 94 94
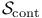 94 94
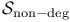 97 97
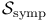 93 93
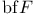 11 11
 94 94
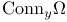 148 148
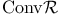 149 149
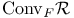 149 149
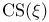 83 83
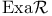 96 96
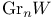 37 37
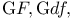 37 37
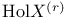 11 11
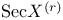 11 11
 148 148
 -pair 125 -pair 125
Almost complex structure 75
Almost complex structure, integrable 75
Almost symplectic structure 75
Almost symplectic structure, integrable 75
Ampleness criterion 165
Balanced path 152
Canonical symplectic structure (form) on  76 76
Canonical symplectic structure (form) on a cotangent bundle 77
Capacious Lie subgroup 133
Characteristic foliation 76
Compatible complex and symplectic structures 73
Complex manifold 75 76
Complex structure 71
Complex subspace 72
Complex vector space 71
Contact cutting-off 92
Contact distribution 82
Contact form 82
Contact Hamiltonian 92
Contact manifold 82
Contact monomorphism 87
Contact structure 4 82
Contact structure, cooriented 83
Contact structure, overtwisted 102
Contact structures, formally homotopic 102
Contact structures, homotopic 102
Contact structures, isotopic 102
Contact vector field 92
Contactization 84
Contactomorphisms 83
Convex integration XII
Convex integration, iterated 160
Convex integration, one-dimensional 149
Convex integration, parametric 155
Coordinate principal subspace 159 162
CR-structure 76
Darboux contact form 82
Darboux' chart 76
Diffeotopy,  -small 20 -small 20
Differential condition 47
Differential inclusion 148
Differential relation XI 47
Differential relation,  -flexible 126 -flexible 126
Differential relation,  -microflexible 125 126 -microflexible 125 126
Differential relation, 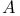 -invariant 133 -invariant 133
Differential relation, ample 148 163
Differential relation, ample in the coordinate directions 159
Differential relation, closed 49
Differential relation, determined XI 49
Differential relation, Diff V-invariant 60
Differential relation, fibered 58
Differential relation, fiberwise path-connected 149
Differential relation, locally integrable 123 124
Differential relation, microflexible 126
Differential relation, open 49
Differential relation, overdetermined 49
Differential relation, underdetermined XI 49
distribution 42
Embedding,  -Lagrangian 3 -Lagrangian 3
Embedding, co-real 170
Embedding, contact 115
Embedding, directed 168
Embedding, isocontact 115
Embedding, isosymplectic 105
Embedding, Lagrangian 3
Embedding, real 3 170
Embedding, symplectic 105
Engel structure 4
Epimorphism 48
Exact Lagrangian immersion 89
Exact Lagrangian submanifold 89
Exact symplectic manifold 140
Family of sections 7
Family of sections, continuous 7
Family of sections, smooth 7
Fiber bundle 7
Fibered map 58
Fibration 7
| Fibration, natural 59
Fibration, trivial 7
Flower 151
Flower, abstract 150
Flower, fibered 155
Formal inverse 172
Formal primitive 43
Formal primitive, Hamiltonian function 91
Formal primitive, time dependent 91
Hamiltonian isotopy 91
Hermitian structure 73 75
Hermitian structure, integrable 75
Holonomic 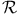 -approximation theorem 127 -approximation theorem 127
Holonomic approximation 19
Holonomic approximation theorem 20
Homotopy principle (h-principle) XI 2 54
Homotopy principle (h-principle) for 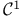 -isometric immersions 182 -isometric immersions 182
Homotopy principle (h-principle) for 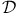 -sections 172 -sections 172
Homotopy principle (h-principle) for ample differential relations 163
Homotopy principle (h-principle) for contact structures on open manifolds 96
Homotopy principle (h-principle) for differential relations over a cube 162
Homotopy principle (h-principle) for directed embeddings 168
Homotopy principle (h-principle) for divergence free vector fields 174
Homotopy principle (h-principle) for generalized isocontact immersions 139
Homotopy principle (h-principle) for generalized isosymplectic immersions 143
Homotopy principle (h-principle) for immersions transversal to contact distribution 131
Homotopy principle (h-principle) for immersions transversal to distribution 65
Homotopy principle (h-principle) for isocontact embeddings 115
Homotopy principle (h-principle) for isocontact immersions 137
Homotopy principle (h-principle) for isosymplectic embeddings 106
Homotopy principle (h-principle) for isosymplectic immersions 142
Homotopy principle (h-principle) for Lagrangian immersions 140
Homotopy principle (h-principle) for Legendrian immersions 138
Homotopy principle (h-principle) for maps transversal to contact distribution 130
Homotopy principle (h-principle) for maximally non-integrable tangent hyperplane distributions on even-dimensional manifold 132 178
Homotopy principle (h-principle) for microflexible 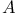 -invariant relations 134 -invariant relations 134
Homotopy principle (h-principle) for microflexible Diff V-invariant relations 128
Homotopy principle (h-principle) for non-vanishing 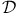 -sections 173 -sections 173
Homotopy principle (h-principle) for open Diff V-invariant relations 60
Homotopy principle (h-principle) for real and co-real embeddings 170
Homotopy principle (h-principle) for real and co-real immersions 168
Homotopy principle (h-principle) for sections transversal to distribution 65
Homotopy principle (h-principle) for subcritical isotropic embeddings 122
Homotopy principle (h-principle) for symplectic structures on open manifolds 95
Homotopy principle (h-principle) for systems of divergence free vector fields 176
Homotopy principle (h-principle) for systems of exact forms 176
Homotopy principle (h-principle) for systems of linearly-independent 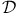 -sections 174 -sections 174
Homotopy principle (h-principle) for two-forms of maximal rank on odd-dimensional manifolds 97 177
Homotopy principle (h-principle), 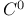 -dense 58 -dense 58
Homotopy principle (h-principle), (multi) parametric 56
Homotopy principle (h-principle), fibered 58
Homotopy principle (h-principle), local 57
Homotopy principle (h-principle), one-parametric 54
Homotopy principle (h-principle), relative 57
Homotopy principle (h-principle), Smale — Hirsch 63
Homotopy, holonomic 11
Homotopy, regular 1 34
Homotopy, tangential 37
Immersion 1 34 48
Immersion relation 48
Immersion,  -coisotropic 167 -coisotropic 167
Immersion,  -isotropic 167 -isotropic 167
Immersion,  -Lagrangian 167 -Lagrangian 167
Immersion, A-directed 39
Immersion, co-real 78
Immersion, coisotropic 78
Immersion, complex 78 168
Immersion, contact 87
Immersion, isocomplex 78
Immersion, isocontact 87 138
Immersion, isometric 1 181
Immersion, isosymplectic 78 143
Immersion, isotropic 78 87
Immersion, Lagrangian 78
Immersion, Legendrian 87
Immersion, real 78 168
Immersion, subcritical 87
Immersion, symplectic 78
Isotopy, Hamiltonian 91
Isotopy, Legendrian 91
Kaehler manifold 75
Kaehler metric 75
Liouville structure 90
Manifold, almost complex 75
Manifold, almost Kaehler 75
Manifold, almost symplectic 75
Manifold, complex 75 76
Manifold, contact 82
Manifold, Hermitian 75
Manifold, Kaehler 75
Manifold, open 35
Manifold, symplectic 75 76
Map, fibered 58
Map, free 3
Map, short 181
Map, strictly short 181
Map, transversal to a distribution 65
Map, transversal to a stratified set 14
Map, transversal to a submanifold 13
Microextension trick 63
Monomorphism 37
Monomorphism, contact 87
Monomorphism, isocontact 87 139
Monomorphism, isosymplectic 106 143
Monomorphism, symplectic 106
Nash — Kuiper theorem 182
Nijenhuis tensor 75
Operator, formally invertible 172
Operator, pure differential 172
Petals 150
Polyhedra 14
Positivity condition 101
Primitive quadratic form 183
Primitive semi-Riemannian metric 183
Principal direction 162
Principal subspace 162
Product of paths, uniform 152
Product of paths, weighted 152
Projectivization 86
r-jet 8 9
r-jet extension 8 10
Reeb foliation 84
Reeb vector field 84
Removal of singularities XII
Riemannian  -manifolds 181 -manifolds 181
Riemannian  -metric 181 -metric 181
Section 7
Section,  -non-singular 49 -non-singular 49
Section, fiberwise holonomic 22
Section, holonomic 11
Section, transversal to a distribution 65
Semi-Riemannian metric 181
Set, ample 148
Set, m-complete 41
Set, stratified 14
Short formal solution 149
Short path 147
Singularity 49
Singularity, thin 163
Singularity, thin in the coordinate directions 160
Smale's sphere eversion 34
Solution 50 51
Solution, formal XI 50 51
Solution, genuine 50
Solution, r-extended 50
Space of complex structures 72
Space of r-jets 8
Space of symplectic structures 70
Stability theorems 80 88
Standard contact structure on 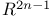 82 82
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



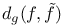


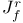
 -mersion
-mersion 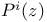
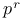

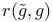
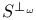
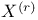
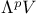
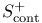
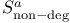
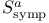
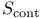
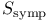
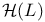
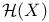
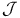
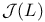
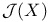
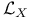
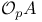
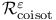
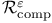
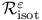
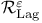
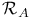
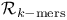
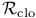



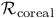
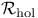
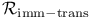
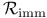

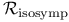
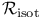

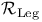

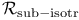
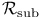
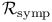

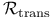
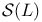
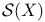
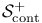
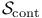
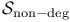
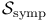
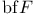

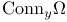
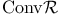
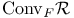
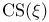
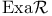
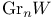
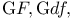
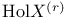
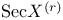

 -pair
-pair 
 -small
-small 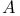 -invariant
-invariant  -Lagrangian
-Lagrangian 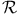 -approximation theorem
-approximation theorem 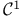 -isometric immersions
-isometric immersions 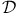 -sections
-sections 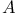 -invariant relations
-invariant relations 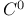 -dense
-dense  -manifolds
-manifolds  -non-singular
-non-singular