|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Гардинер К.В. — Стохастические методы в естественных науках |
|
|
 |
| Предметный указатель |
Стохастическое дифференциальное уравнение, разложение по малому шуму 230—239
Стохастическое дифференциальное уравнение, связь с УФП 136
Стратоновича стохастический интеграл 124
Теорема регрессии 99
Теорема регрессии квантовая 484 485
Термостат, определение 466
Тримолекулярная реакция как предел бимолекулярной реакции 358—363
Управляющее уравнение 82 291
Управляющее уравнение в случае многих переменных 321
Управляющее уравнение в случае многих переменных для системы с диффузией 373 374
Управляющее уравнение в случае многих переменных, разложение Крамерса — Мойала 326
Управляющее уравнение в фазовом пространстве 401
Управляющее уравнение диффузии, непрерывная форма 374—379
Управляющее уравнение квантовое для гармонического осциллятора 473—477
Управляющее уравнение квантовое, вывод 468—473
Управляющее уравнение квантовое, определение 472
Управляющее уравнение разложения по обратному размеру системы 375
Управляющее уравнение рождения-гибели 30 34
Управляющее уравнение рождения-гибели для квантового гармонического осциллятора 473
Управляющее уравнение рождения-гибели для одной переменной 292
Управляющее уравнение рождения-гибели и бистабильность 429—431
Управляющее уравнение рождения-гибели, разложение по обратному размеру системы 326
Управляющее уравнение, аппроксимация уравнением Фоккера — Планка 303
Управляющее уравнение, описывающее реакции и диффузию 480
Управляющее уравнение, описывающее реакции и диффузию, разложение по обратному размеру системы 380
Управляющее уравнение, разложение по обратному размеру системы 308—316
Управляющее уравнение, случай одной переменной, стационарное решение 293—295
Управляющее уравнение, среднее время достижения границ 318—321
Управляющее уравнение, стационарные решения без учета детального баланса 325
Усреднение по ансамблю 39
УФП см. «Фоккера — Планка уравнение»
Феноменологическая сила 210
Феноменологический поток 210
Флуктации критические 314
Флуктации критические и разложение по обратному размеру системы 314
Флуктации локальные и глобальные 389
Флуктуационно-диссипационная теорема, применение 211
Фоккера — Планка уравнение 160
Фоккера — Планка уравнение в P-представлении 476 496
Фоккера — Планка уравнение в комплексном P-представлении 498
Фоккера — Планка уравнение в комплексном P-представлении, условие потенциальности 500—502
Фоккера — Планка уравнение в положительном P-представлении 498—500
Фоккера — Планка уравнение с одной переменной 166
Фоккера — Планка уравнение с одной переменной, потенциальное решение 168 169
Фоккера — Планка уравнение с одной переменной, собственные функции 174—181
Фоккера — Планка уравнение с одной переменной, среднее время достижения границ 183
Фоккера — Планка уравнение со многими переменными, собственные функции 214
Фоккера — Планка уравнение со многими переменными, стационарные решения 193 194
Фоккера — Планка уравнение со многими переменными, условие потенциальности 193
Фоккера — Планка уравнение химическое 326
Фоккера — Планка уравнение, вариационный принцип для собственных функций 217
Фоккера — Планка уравнение, граница входная 166
Фоккера — Планка уравнение, граница естественная 166
| Фоккера — Планка уравнение, разложение по малому шуму 239
Фоккера — Планка уравнение, стационарное распределение, асимптотический метод 246
Хакена модель 278
Хаос 19
Характеристическая функция 59
Характеристическая функция гауссова распределения 64
Характеристическая функция и моменты 59
Характеристическая функция квантовая 464 465
Химическая реакция  в представлении Пуассона 358 359 в представлении Пуассона 358 359
Химическая реакция  , , 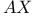 365 365
Химическая реакция  , , 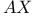 , управляющее уравнение 298 299 , управляющее уравнение 298 299
Химическая реакция 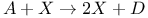 , ,  , решение управляющего уравнения 334—336 , решение управляющего уравнения 334—336
Химическая реакция  , ,  пространственно-распределенная 393—397 пространственно-распределенная 393—397
Химическая реакция  , ,  , комплексное представление Пуассона 344—346 , комплексное представление Пуассона 344—346
Химическая реакция  , ,  , положительное представление Пуассона 350 , положительное представление Пуассона 350
Химическая реакция  , ,  , решение в представлении Пуассона 340—343 , решение в представлении Пуассона 340—343
Химическая реакция 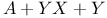 , , 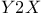 , исключение промежуточного соединения 359—363 , исключение промежуточного соединения 359—363
Химическая реакция  , ,  пространственно-распределенная 38—393 пространственно-распределенная 38—393
Химическая реакция 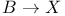 , ,  и положительное представление Пуассона 350 351 и положительное представление Пуассона 350 351
Химическая реакция 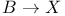 , ,  , комплексное представление Пуассона 346 347 , комплексное представление Пуассона 346 347
Химическая реакция 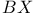 , , 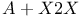 , аналогия с гармоническим осциллятором 474 , аналогия с гармоническим осциллятором 474
Химическая реакция 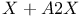 , УФП 171 , УФП 171
Химическая реакция 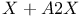 , УФП химическое 327—333 , УФП химическое 327—333
Химическая реакция 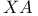 и разложение по обратному размеру системы 310 и разложение по обратному размеру системы 310
Химическая реакция 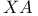 , управляющее уравнение 295 , управляющее уравнение 295
Химическая реакция 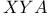 273 273
Химическая реакция 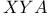 , химическое УФП 327—333 , химическое УФП 327—333
Химическая реакция  , как система с реакциями и диффузией 382—386 , как система с реакциями и диффузией 382—386
Химическая реакция  , решение управляющего уравнения 337 338 , решение управляющего уравнения 337 338
Химическая реакция  , уравнение реакции с диффузией 381 , уравнение реакции с диффузией 381
Химическая реакция в системе «хищник—жертва», УФП 328—333
Химическая реакция мономолекулярная 340
Химическая реакция нелокальная 397
Химическая реакция, исключение короткоживущих промежуточных продуктов 273
Химическая реакция, связь между локальным и глобальным описанием 398—402
Химические реакции, теория переходного состояния 424
Химическое уравнение реакции с диффузией 370
Химотрипсиноген, обратимая денатурация 426
Центральная предельная теорема 65
Чепмена — Колмогорова уравнение 24 72 73
Чепмена — Колмогорова уравнение дифференциальное 76—82
Чепмена — Колмогорова уравнение дифференциальное обратное 87
Шредингера уравнение 451
Шум 31
Шум белый 40—44 117—120
Шум белый как предел цветного шума 264
Шум дробовой 32
Шум тепловой 40—44
Шум третьего порядка 359
Шум третьего порядка, определение 363 364
Эйнштейна уравнение и двухуровневый атом 481
Эргодичность 39
Эрмита полиномы 179
Эрмита полиномы при адиабатическом исключении 255
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 в представлении Пуассона
в представлении Пуассона 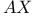
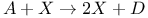 ,
,  , решение управляющего уравнения
, решение управляющего уравнения  ,
, 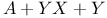 ,
, 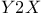 , исключение промежуточного соединения
, исключение промежуточного соединения 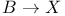 ,
,  и положительное представление Пуассона
и положительное представление Пуассона 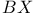 ,
, 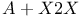 , аналогия с гармоническим осциллятором
, аналогия с гармоническим осциллятором 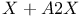 , УФП
, УФП 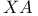 и разложение по обратному размеру системы
и разложение по обратному размеру системы 
 , как система с реакциями и диффузией
, как система с реакциями и диффузией  , решение управляющего уравнения
, решение управляющего уравнения